Презентация на тему: Основы логики - построение таблиц истинности

ОСНОВЫ ЛОГИКИ Построение таблиц истинности Кривенцов Леонид Александрович, учитель информатики и ИКТ МОУ-СОШ №4 г. Асино томской области

При изучении работы различных устройств компьютера приходится рассматривать такие его логические элементы, в которых реализуются сложные логические выражения. Поэтому необходимо научиться определять результат этих выражений, то есть строить для них таблицы истинности. Таблица истинности – это таблица, в левой части которой записывается набор аргументов, а в правой части - соответствующие значения логической функции.

Алгоритм построения таблиц истинности для сложных выражений: Определить количество переменных (простых выражений); Определить количество логических операций и последовательность их выполнения. Определить количество строк: количество строк = 2ª + строка для заголовка, где a – количество логических переменных. Определить количество столбцов: количество столбцов = количество переменных + количество логических операций; Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности с учетом таблиц истинности основных логических операций.

Порядок выполнения логических операций: Действия в скобках Инверсия Конъюнкция Дизъюнкция

Рассмотрим пример построения таблицы истинности для следующего сложного (составного) логического выражения: Определяем приоритетность выполнения логических операций

Решение: Простые выражения (логические переменные): А, В, С; (3) Количество логических операций: ¬ А - инверсия; B C - операция дизъюнкции; ¬ А & (B C). операция конъюнкции. Всего: 3 Количество строк: на входе три простых высказывания: А, В, С , поэтому a=3 и количество строк = 2³ +1 = 9. Количество столбцов: 3+3=6 Заполняем столбцы с учетом таблиц истинности логических операций.

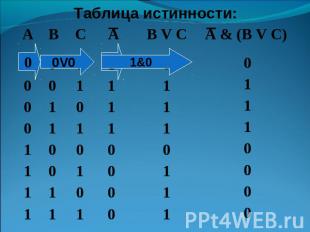
Таблица истинности:

Постройте таблицу истинности для логического выражения: D=А V B & C

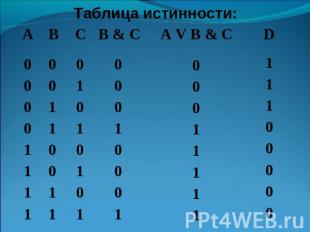
Таблица истинности:

Домашнее задание: Изучите новый материал по конспекту в тетради; 2. Постройте таблицу истинности для логического выражения: D=А V B & C