Презентация на тему: Медианы, биссектрисы и высоты треугольника

«Перпендикуляр к прямой. Медианы, биссектрисы, высоты треугольника»




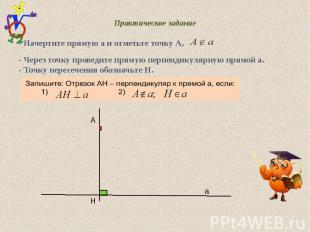
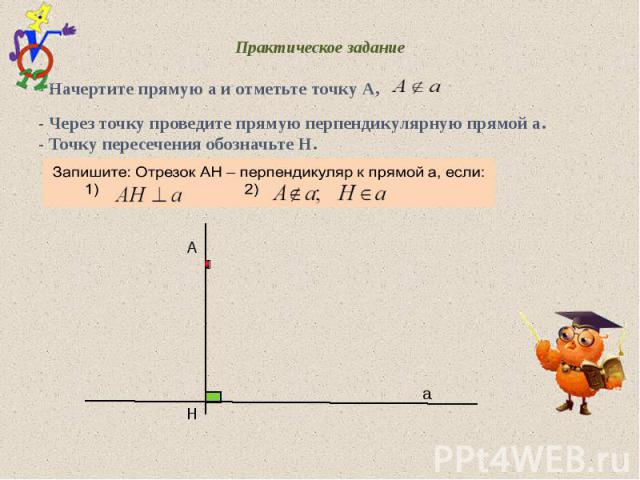
Практическое задание - Начертите прямую а и отметьте точку А, - Через точку проведите прямую перпендикулярную прямой а. - Точку пересечения обозначьте Н. А


Докажем теорему о существовании перпендикуляра к прямой. Теорема: Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой и притом один. Доказательство. Пусть A – точка, не лежащая на данной прямой a (рис. а). Докажем сначала, что из точки A можно провести перпендикуляр к прямой a. Мысленно перегнем плоскость по прямой a (рис. б) так, чтобы полуплоскость с границей a, содержащая точку A, наложилась на другую полуплоскость. При этом точка A наложится на некоторую точку. Обозначим ее буквой B. Разогнем плоскость и проведем через точки A и B прямую. Пусть H – точка пересечения прямых AB и a (рис. в). При повторном перегибании плоскости по прямой a точка H останется на месте. Поэтому луч HA наложится на луч HB, и, следовательно, угол 1 совместится с углом 2. Таким образом, ∠1 = ∠2. Так как углы 1 и 2 – смежные, то их сумма равна 180°, поэтому каждый из них – прямой. Следовательно, отрезок AH – перпендикуляр к прямой a.

Докажем, что из точки A можно провести только один перпендикуляр к прямой . Если предположить, что через точку A можно провести еще один перпендикуляр АН1 к прямой ВС, то получим, что две прямые АН и АН1, перпендикулярные к прямой ВС, пересекаются. Но в п.12 было доказано, что это невозможно (две прямые перпендикулярные к третьей не пересекаются.) Итак, из точки А можно провести только один перпендикуляр к прямой АВ Теорема доказана.


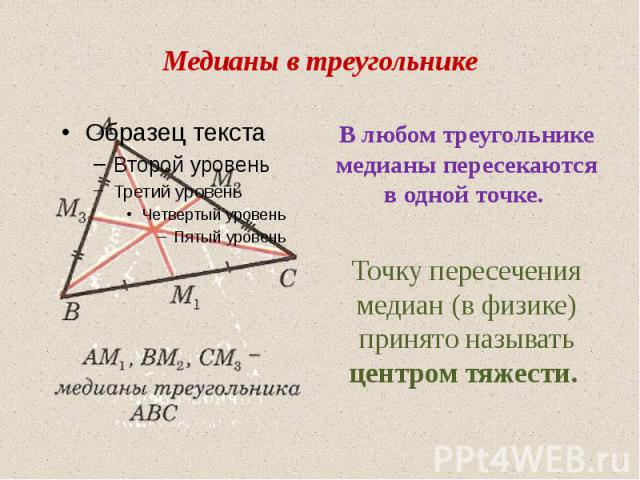
Медианы в треугольнике В любом треугольнике медианы пересекаются в одной точке. Точку пересечения медиан (в физике) принято называть центром тяжести.

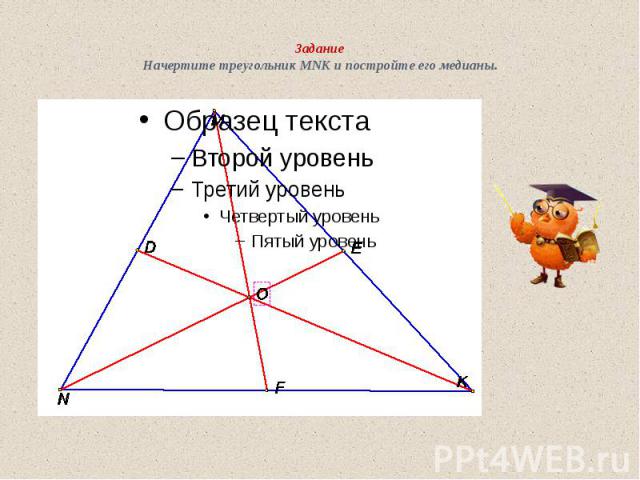
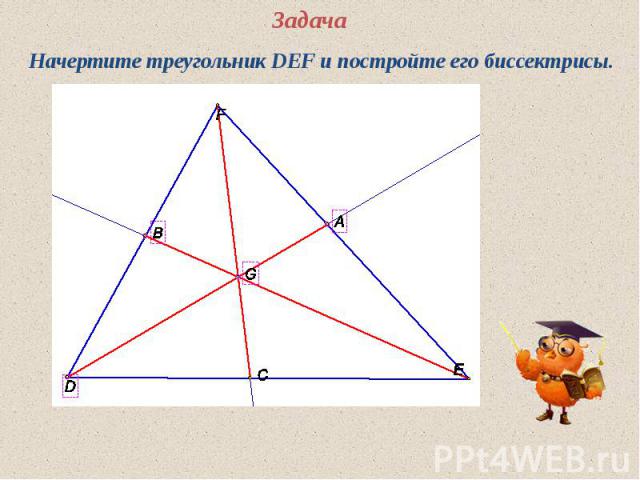
Задание Начертите треугольник MNK и постройте его медианы.
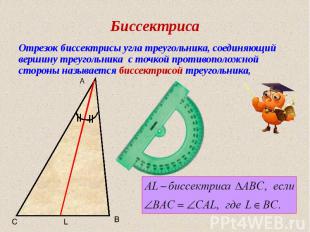
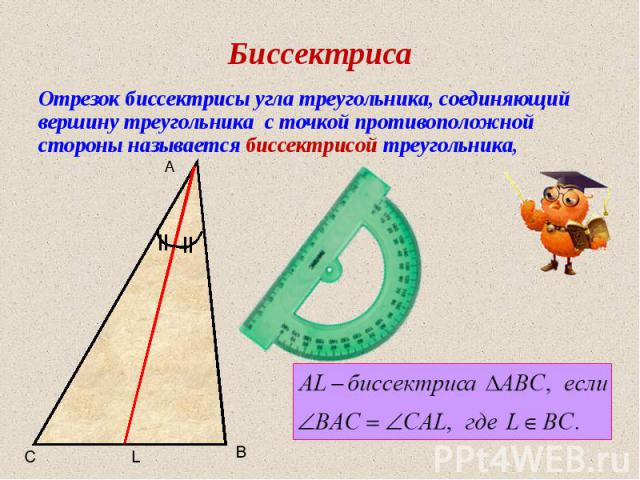
Биссектриса Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны называется биссектрисой треугольника, A
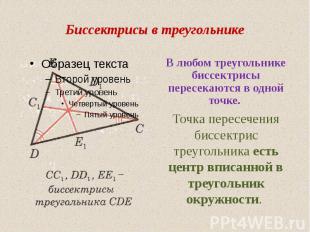
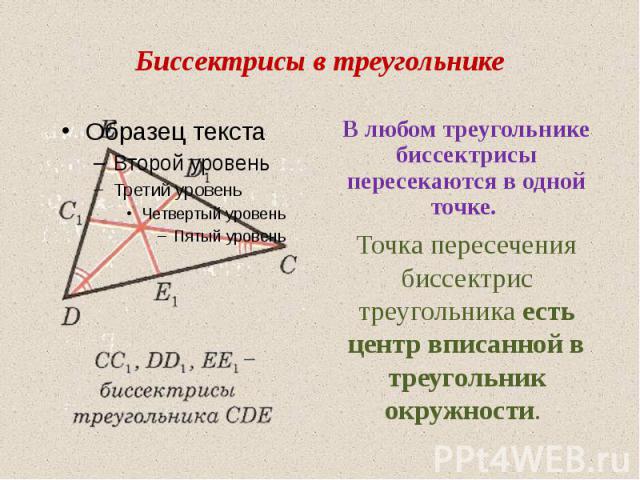
Биссектрисы в треугольнике В любом треугольнике биссектрисы пересекаются в одной точке. Точка пересечения биссектрис треугольника есть центр вписанной в треугольник окружности.
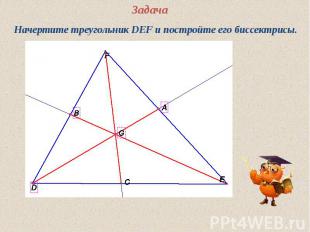

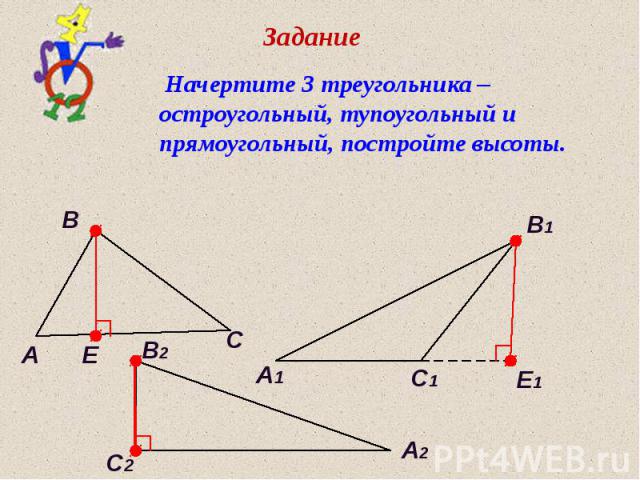
Высота Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону называется высотой треугольника
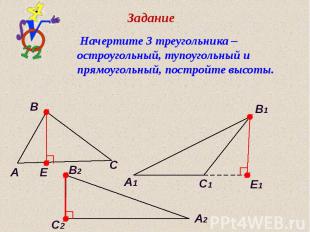

Высоты в треугольнике

Закрепление изученного материала 1.Решить задачи №105 (б), 106 (б) письменно. 2.Решите задания с самопроверкой Дано: АО-медиана АВС, АО =ОК, АВ =6,3 см, ВС=6,5 см, АС =6,7 см. Найдите: СК а)6,4 см; б) 6,7 см; в) 6,5 см; г) 6,3 см. Дано: ОН и ОN - высоты МОК и ЕОF, ОН = ОN , ЕN = 7,8 см, ОЕ= 8,6 см, НМ = 6,3 см. Найдите МК. а)13, 9 см; б) 14,1 см; в) 14,9 см; г) 16,4 см. В треугольниках АВС и КРМ проведены биссектрисы ВО и РЕ, причем АВО = КРЕ. Найдите отрезок ЕМ, если АС =9 см, а EM больше KE на 3,8 см. а)6,4 см; б) 5,4 см; в) 2,6 см; г) 4,8 см.


Домашнее задание П. 16,17, вопросы 5-9 стр. 50 № 106 (а), 106 (а) № 61, 63, 63 (из рабочих тетрадей)