Презентация на тему: Оригаметрия

Оригаметрия Рук. Золотарева Т.Ю.

В математике есть своя красота , как в живописи и поэзии. Н.Е. ЖуковскийОригами-Японское искусство складывания различных фигурок из листков очень тонкой бумаги.

Цели Познакомиться с современной наукой -оригаметриейНаучиться читать чертежи, по которым складываются фигурыУзнать аксиомы и основные приемы изготовления фигур из бумаги

Задачи Познакомиться с одним из разделов математики- оригаметрияРасширить сферу применения математических знанийПознакомиться на практике с основными геометрическими понятиямиУбедиться в необходимости владения конкретными математическими знаниями для применения в практической деятельностиУлучшить пространственное воображение Расширить представления о применении геометрии в искусстве, производстве, быту

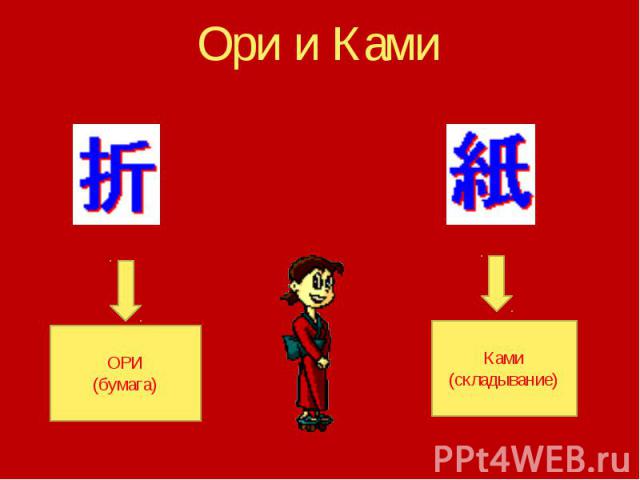
Немного истории Слово Оригами в переводе с японского означает «сложенный из бумаги».В японском языке его пишут с помощью двух иероглифов: ОРИ-бумага и КАМИ- сложенный. История возникновения ОРИГАМИ неразрывно связана с изобретением бумаги. Человечество за время своего развития изобрело много различных материалов для письма. Это папирус, глиняные таблички, береста, бамбуковые планки, пергамент и только в начале первого тысячелетия в Китае изобрели бумагу. Китайцы изготавливали бумагу из бамбуковых стеблей. Скоро секрет изготовления бумаги стал известен в Японии. Японцы улучшили технологию производства и стали получать бумагу прочнее и качественнее китайской. Лучшую бумагу в Японии делали из коры шелковичного дерева. Такая бумага уже обладала свойствами необходимыми для складывания из нее фигурок.

Ори и Ками

Лев Толстой и оригами В 1896 Толстой в своей известной статье «Что такое искусство» неожиданно обращается к искусству оригами. «…одна дама научила меня делать из бумаги, складывая и выворачивая её известным образом, петушков ,которые, когда их дергаешь за хвост, махают крыльями. Выдумка эта от Японии. Я много раз делал этих петушков детям, и не только дети,, но всегда овсе присутствующие большие, не знавшие этих петушков, и господа, и прислуга развеселялись и сближались от этих петушков, все улыбались и радовались: как похоже на птицу эти петушки махают крыльями. Тот, кто выдумал такого петушка, от души радовался, что ему так удалось сделать подобие птицы, и чувство это передается, и потому, как ни странно сказать, произведение такого петушка есть настоящее искусство. Не могу не заметить при этом, что это единственное новое произведение в области бумажных петушков, которое я узнал за 60 лет…»

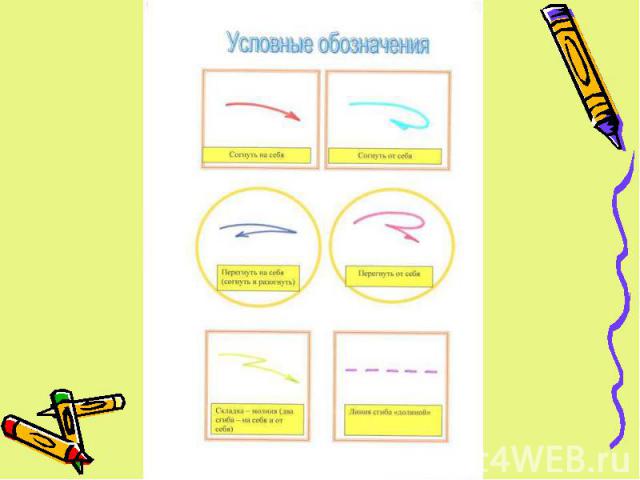
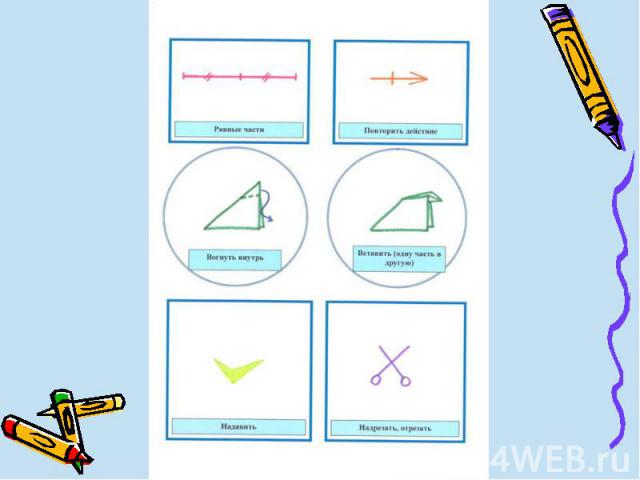
Аксиомы Существует единственный сгиб:Проходящий через две данные точкиСовмещающий две данные точкиСовмещающий две данные прямыеПроходящий через данную точку и перпендикулярный данной прямойПроходящий через данную точку и помещающий другую данную точку на данную прямуюПомещающий каждую из двух данных точек на одну из двух данных прямых

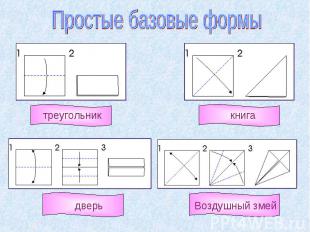
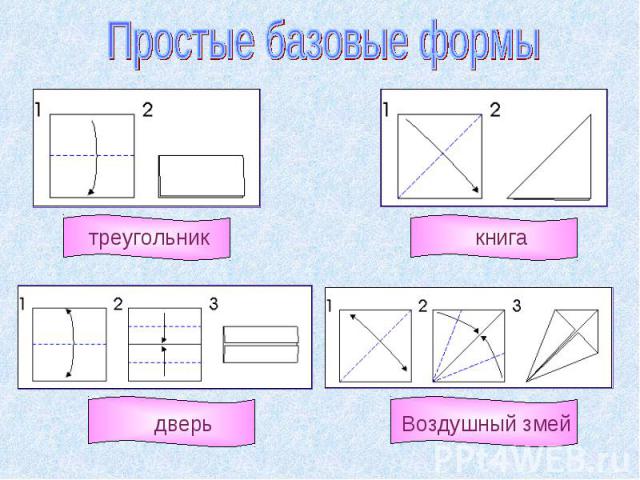
Простые базовые формы

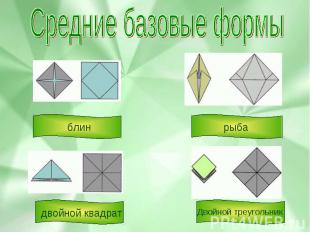
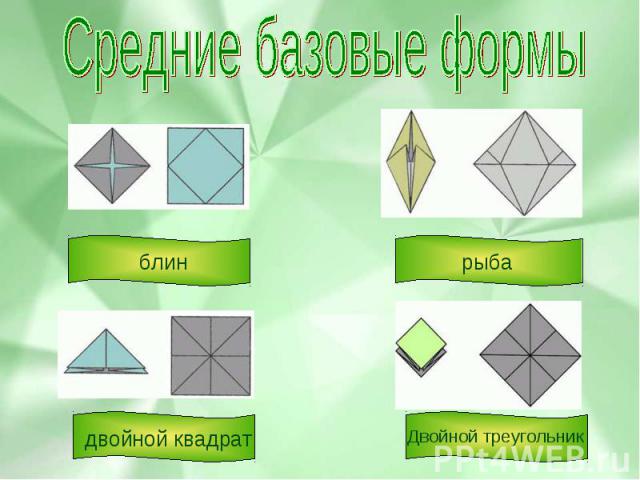
Средние базовые формы

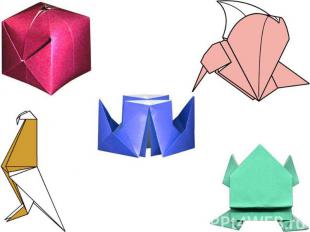
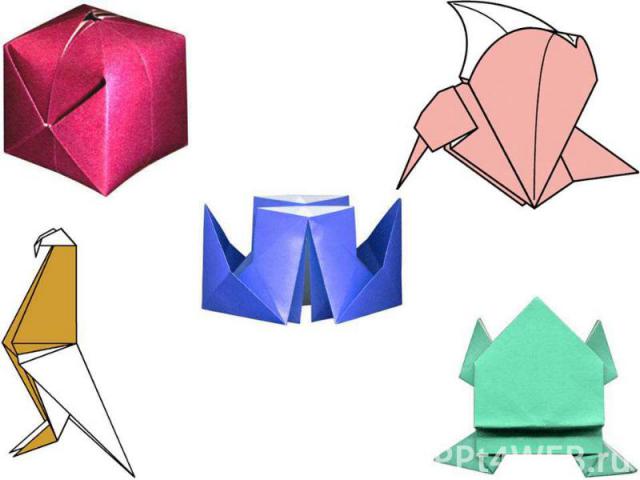
Сложные базовые формы

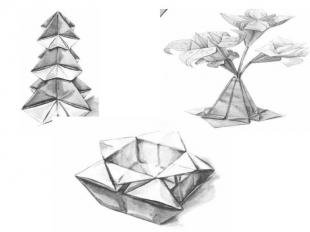
Японские журавлики Каждый японец и каждый, кто брался за оригами, знает историю Садако, девочки из Хиросимы, которая делала журавликов, веря, что это спасет ее от лучевой болезни. Кто-то сказал ей, что если она сделает тысячу журавликов, она поправится. Садако скоро поняла, что ей уже не станет лучше, она умрет. И тогда она стала дарить журавликов другим больным - каждый журавлик, которого сворачивала маленькая Садако, был молитвой: молитвой о спасении человека. На Востоке журавль издавна символизирует жизнь и надежду. История двенадцатилетней Садако превратила фигурку журавля в символ совсем другого рода

Техническим приёмом, порой применяемым в оригами, является выворачивание фигурки или её части наизнанку. Естественно, это удаётся сделать только тогда, когда эта часть состоит как минимум из двух слоёв бумаги. Приём и результат выворачивания бумаги можно посмотреть на моделях кусудам - «шаров».

Оригами в математике

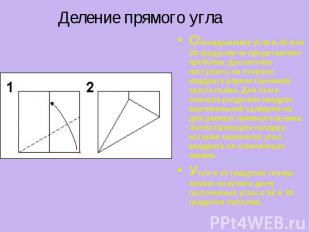
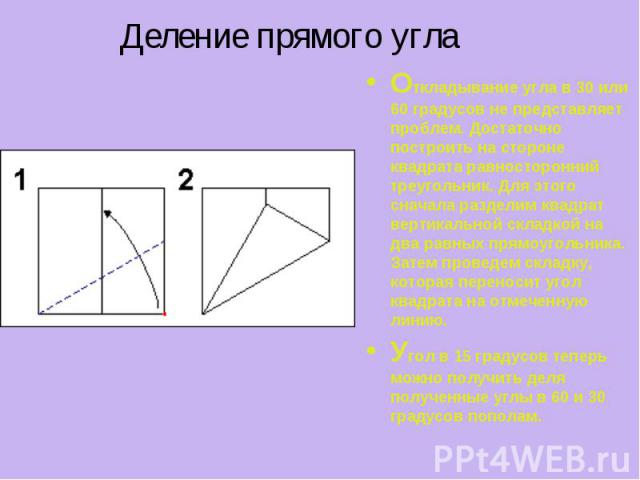
Деление прямого угла Откладывание угла в 30 или 60 градусов не представляет проблем. Достаточно построить на стороне квадрата равносторонний треугольник. Для этого сначала разделим квадрат вертикальной складкой на два равных прямоугольника. Затем проведем складку, которая переносит угол квадрата на отмеченную линию. Угол в 15 градусов теперь можно получить деля полученные углы в 60 и 30 градусов пополам.

Деление листа бумаги Деление листа бумаги на две части не представляет сложности, поскольку реализуется просто складыванием базовой формы книжка. Перейдем к более сложной задаче деления квадратного листа на три части.                           Эта задача уже не столь проста. Для ее решения нам потребуется теорема Хага. Сложим угол квадрата к середине противоположной стороны. В таком случае точка пересечения другой стороны, противоположной этому углу и стороны, прилегающей к нему делит сторону в отношении один к двум. Таким образом, с помощью только складок мы нашли треть стороны квадрата.                    

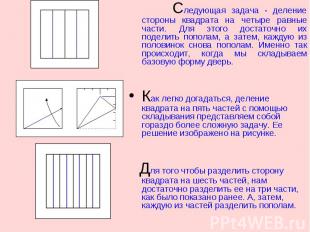
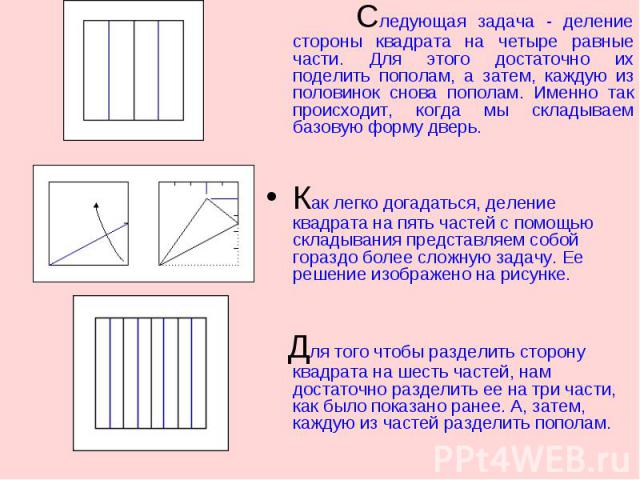
Следующая задача - деление стороны квадрата на четыре равные части. Для этого достаточно их поделить пополам, а затем, каждую из половинок снова пополам. Именно так происходит, когда мы складываем базовую форму дверь.Как легко догадаться, деление квадрата на пять частей с помощью складывания представляем собой гораздо более сложную задачу. Ее решение изображено на рисунке.             Для того чтобы разделить сторону квадрата на шесть частей, нам достаточно разделить ее на три части, как было показано ранее. А, затем, каждую из частей разделить пополам.

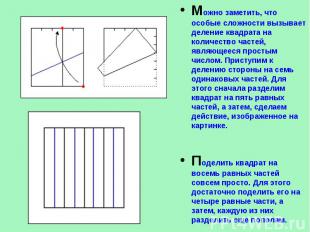
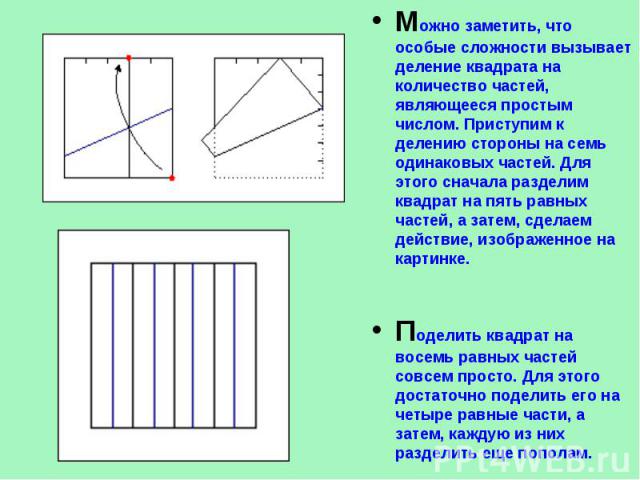
Можно заметить, что особые сложности вызывает деление квадрата на количество частей, являющееся простым числом. Приступим к делению стороны на семь одинаковых частей. Для этого сначала разделим квадрат на пять равных частей, а затем, сделаем действие, изображенное на картинке. Поделить квадрат на восемь равных частей совсем просто. Для этого достаточно поделить его на четыре равные части, а затем, каждую из них разделить еще пополам.

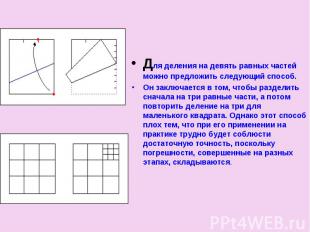
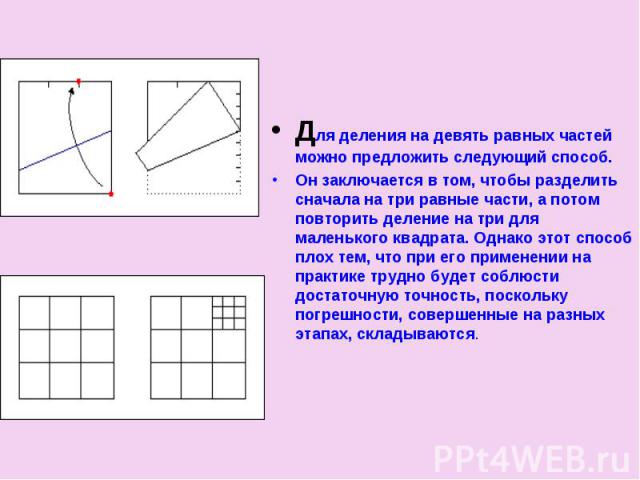
Для деления на девять равных частей можно предложить следующий способ.Он заключается в том, чтобы разделить сначала на три равные части, а потом повторить деление на три для маленького квадрата. Однако этот способ плох тем, что при его применении на практике трудно будет соблюсти достаточную точность, поскольку погрешности, совершенные на разных этапах, складываются.                                       

Оригами в жизни человека. ПедагогикаДизайн жилищаМоделированиеУкрашение и аксессуарыОформительная деятельность

Первые попытки использовать оригами в педагогической практике в Европе справедливо связывают с именем немецкого гуманиста Фридриха Вильгельма Августа Фребеля (1792-1852). Именно он в начале XIX века начал создавать детские сады, а затем и школу. Фребель считает Природу лучшим учителем. Он сам сначала был лесником, очень любил и ценил природу и поэтому не хотел, чтобы в школе дети занимались зубрёжкой. Фребель считал, что жизнь, движение и знание есть три главные составляющие развития Человека. Его теория взглядов на образование и развитие личности включает в себя 4 главных компонента: 1.Свободная активность. 2.Творчество.3. Участие в жизни общества.4. Мышечная активность.

Чаще всего оригами преподают детям в детских садах, начальной школе и различных кружках домов творчества. Целью таких занятий является не складыва-ние как можно большего количества разнообраз-ных фигурок, а развитие у детей целого ряда способностей и навыков

Педагогами многих стран давно замечено, что оригами: учит слушать устные инструкции учителя;учит совершать последовательные действия;развивает способность контролировать с помощью мозга тонкие движения рук и пальцев;улучшает пространственное воображение и умение мысленно оперировать с объемными предметами;учит читать чертежи, по которым складываются фигурки;знакомит на практике с основными геометрическими понятиями;развивает уверенность в своих силах и способностях;помогает развитию первых чертежных навыков;стимулирует развитие памяти;учит концентрировать внимание;развивает творческие способности и исследовательские навыки;улучшает глазомер;снижает тревожность.Практически все занимающиеся преподаванием оригами педагоги отмечают положительное влияние этого занятия на успехи своих учеников и по остальным предметам. Занятия складыванием способствуют развитию психологических контактов между учителем и учениками.

Дизайн жилища

Моделирование

Украшения и аксессуары

Вывод Оригаметрия-1.Развивает способность контролировать с помощью мозга тонкие движения рук и пальцев2.Улучшает пространственное воображение и умение мысленно оперировать с объемными предметами3.Учит читать чертежи, по которым складываются фигуры4.Знакомит на практике с основными геометрическими понятиями5.Развивает творческие способности

Список литературы 1. Афонькин, С. Ю., Капитонова, И. В. Оригами и геометрия. – Чебоксары: ЧГУ, 1993. – 28 с.2. Белим, С. Н. Задачи по геометрии, решаемые методами складывания (оригами). – М.: Аким, 1997. – 64 с.3. Оригами помогает геометрии. под ред. Н. И. Чиканцевой. – М.: МГПУ, 1995. – 30 с.4. Афонькин, С. Ю., Афонькина, Е. Ю. Все об оригами. – СПб: ООО «СЗКЭО «Кристалл»», 2004. – 272 с., ил.5. Уроки оригами в школе и дома: учебное пособие.6. Журнал «Оригами. Искусство складывания из бумаги.7. Выгонов, В. В. Мир оригами 1–2. – М.: Новая школа, 1996. – 56 с.8. Кочетков, Е., Шумакова, Ю. Мир бумаги. Цветы. – Ростов-на-Дону: Издательско-полиграфическое объединение «Южный регион», 1996.9. Кошелев, В. М., Афонькин, С. Ю. Вырезаем и складываем. – СПб.: Кристалл, 1999. – 160 с.10. Лутошкина, Ю. Г. Волшебный квадратик. Оригами-сказка. – Чебоксары: Чувашия, 1997. – 36 с.11. Соколова, С. В. Игрушки-оригамушки. Вып. 1-2 – СПб.: Химия, 1997–98 гг. – 32 с., 40 с.12. Хлямова, Т. В. Звездное небо оригами – М.: Аким, 1997. – 64 с.13. Хьюстон Сара, Джонсон Пол. Смастери себе игрушку без клея и ножниц. Бумажный зверинец. – М.: Махаон, 1997.14. Афонькин, С. Ю., Афонькина, Е. Ю. Оригами в вашем доме. – М.: Легкая промышленность, 1995. – 32 с.15. Афонькин, С. Ю., Афонькина, Е. Ю. Оригами на праздничном столе. – М.: Аким, 1995. – 32 с.16. Афонькин, С. Ю., Афонькина, Е. Ю. Цветущий сад оригами. – СПб.: Химия, 1995. – 56 с.17. Афонькин, С. Ю., Афонькина, Е. Ю. Оригами. Самолеты и пароходы. – СПб.: Химия, 1996. – 64 с.18. Афонькин, С. Ю., Афонькина, Е. Ю. Кусудамы – волшебные шары. – М.: Аким, 1997. – 64 с.19. Афонькин, С. Ю., Лежнева, Л. В., Пудова, В. П. Оригами и аппликация. – Спб.: ООО Издательство «Кристалл», 1998. – 304 с.

Конец.