Презентация на тему: Логика. Понятие, суждение, умозаключение

ЛогикаПонятие, суждение, умозаключение Комкова Мария СергеевнаУчитель информатикиГимназия МИИТ г. Москва

Понятие - это форма мышления, отражающая наиболее существенные свойства предмета, отличающие его от других предметов

Алгебра множеств Алгебра множеств, одна из основополагающих современных математических теорий, позволяет исследовать отношения между множествами и, соответственно, объемами понятий.

Между множествами (объемами понятий) могут быть различные виды отношений: равнозначность, когда объемы понятий полностью совпадают; пересечение, когда объемы понятий частично совпадают; подчинения, когда объем одного понятия полностью входит в объем другого и т.д.

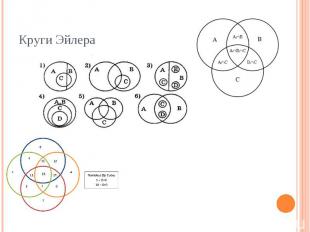
Круги Эйлера

Высказывание (суждение) - это форма мышления, выраженная с помощью понятий, посредством которой что-либо утверждают или отрицают о предметах, их свойствах и отношениях между ними.

Высказывание может быть истинным или ложным.

Высказывание называется простым, если никакая его часть сама не является высказыванием. Высказывание, состоящее из простых высказываний, называются составным (сложным).

Умозаключение - это форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, по определенным правилам логического вывода получается новое знание о предметах реального мира (вывод).

Практическая часть. Пример 1. Установите, какие из следующих предложений являются логическими высказываниями, а какие — нет (объясните почему): а) “Солнце есть спутник Земли”; б) “2+3=4”; в) “сегодня отличная погода”; г) “в романе Л.Н. Толстого “Война и мир” 3 432 536 слов”; д) “Санкт-Петербург расположен на Неве”; е) “музыка Баха слишком сложна”; ж) “первая космическая скорость равна 7.8 км/сек”; з) “железо — металл”; и) “если один угол в треугольнике прямой, то треугольник будет тупоугольным”; к) “если сумма квадратов двух сторон треугольника равна квадрату третьей, то он прямоугольный”.

Пример 2. Укажите, какие из высказываний предыдущего упражнения истинны, какие — ложны, а какие относятся к числу тех, истинность которых трудно или невозможно установить.

Пример 3. Приведите примеры истинных и ложных высказываний: а) из арифметики;   б) из физики; в) из биологии;   г) из информатики; д) из геометрии;   е) из жизни.

Пример 4. Сформулируйте отрицания следующих высказываний или высказывательных форм: а) “Эльбрус — высочайшая горная вершина Европы”; б) “2>=5”; в) “10<7”; г) “все натуральные числа целые”; д) “через любые три точки на плоскости можно провести окружность”; е) “теннисист Кафельников не проиграл финальную игру”; ж) “мишень поражена первым выстрелом”; з) “это утро ясное и теплое”; и) “число n делится на 2 или на 3”; к) “этот треугольник равнобедренный и прямоугольный”; л) "на контрольной работе каждый ученик писал своей ручкой

Пример 5. Определите, какие из высказываний (высказывательных форм) в следующих парах являются отрицаниями друг друга, а какие нет: а) “5<10”, “5>10”; б) “10>9”, “10<=9”; в) “мишень поражена первым выстрелом”, “мишень поражена вторым выстрелом”; г) “машина останавливалась у каждого из двух светофоров”, “машина не останавливалась у каждого из двух светофоров”, д) “человечеству известны все планеты Солнечной системы”, “в Солнечной системе есть планеты, неизвестные человечеству”; е) “существуют белые слоны”, “все слоны серые”; ж) “кит — млекопитающее”, “кит — рыба”; з) “неверно, что точка А не лежит на прямой а”, “точка А лежит на прямой а”;

Пример 6. Определите значения истинности высказываний: а) “наличия аттестата о среднем образовании достаточно для поступления в институт”; б) “наличие аттестата о среднем образовании необходимо для поступления в институт”; в) “если целое число делится на 6, то оно делится на 3”; г) “подобие треугольников является необходимым условием их равенства”; д) “подобие треугольников является необходимым и достаточным условием их равенства”;