Презентация на тему: Величие числа

Выполнили: обучающиеся 8 класса НОУ СОШ “Вайда” Полякова Елизавета, Третьякова Ольга

Цели работы: - дать представление о кодировании информации в компьютере; расширить и систематизировать знания о числе, системах счисления; сформировать умение решать задачи по переводу числа из одной системы счисления в другую; продолжить формирование ведущих компонентов компьютерной грамотности.

Содержание:

Кодирование информации

Понятие о кодировании Кодирование - процесс представления информации в виде кода. Код - набор условных обозначений для представления информации. Для представления информации могут использоваться разные коды и, соответственно, надо знать определенные правила: законы записи этих кодов.

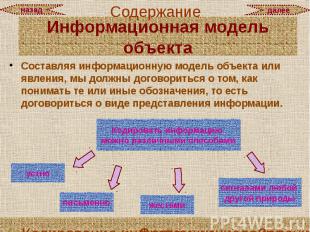
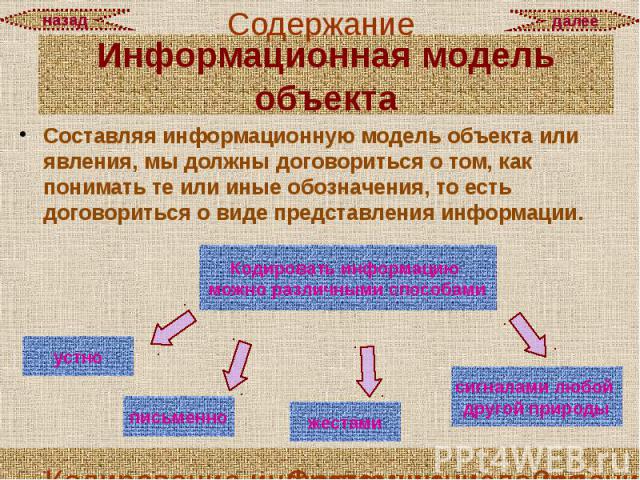
Составляя информационную модель объекта или явления, мы должны договориться о том, как понимать те или иные обозначения, то есть договориться о виде представления информации. Составляя информационную модель объекта или явления, мы должны договориться о том, как понимать те или иные обозначения, то есть договориться о виде представления информации.

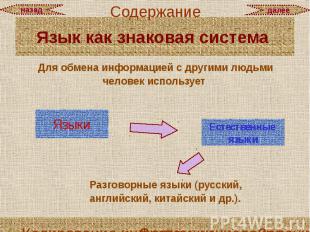
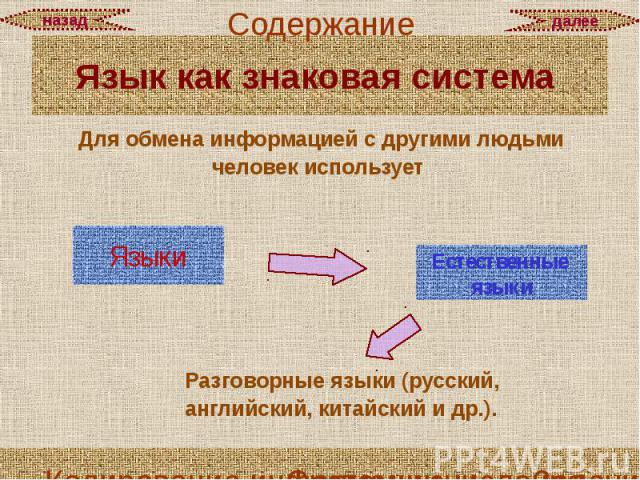
Язык как знаковая система Для обмена информацией с другими людьми человек использует

Язык как знаковая система

Язык как знаковая система В основе языка лежит алфавит, то есть набор символов (знаков), которые человек различает по их начертанию.

Некоторые языки используют в качестве знаков не буквы и цифры, а другие символы, например, химические формулы, ноты, изображения элементов электрических или логических схем, дорожные знаки, точки и тире (код азбуки Морзе) и др.. Некоторые языки используют в качестве знаков не буквы и цифры, а другие символы, например, химические формулы, ноты, изображения элементов электрических или логических схем, дорожные знаки, точки и тире (код азбуки Морзе) и др..

Системы счисления Системы счисления можно рассматривать как формальные языки, имеющие алфавит (цифры) и позволяющие не только именовать и записывать объекты (числа), но и выполнять над ними арифметические операции по строго определенным правилам.

Из истории кодирования Счет по пальцам Считать люди научились еще в незапамятные времена. Сначала они различали просто один предмет или много предметов. С возникновением скотоводства, земледелия, обмена, торговли возникла необходимость счета. Для такого счета, характерно отсутствие названия чисел, употребляли их только с именем 'две моркови', но не 'два'. Наиболее простой 'счетной машиной' издавна были пальцы рук и ног.

Зарубки Для хранения числовой информации делали зарубки на деревьях и палках. Последние в России назывались бирками. В истории, народном творчестве и в литературных произведениях много раз упоминается о счете при помощи зарубок и, в частности, при помощи бирок.

Веревочно-узловой счет (верёвочные узлы) Аборигены Южной Америки считали и вычисляли при помощи системы узлов, завязанных на веревках или ремнях. Такие приспособления для веревочно-узлового счета назывались квипу. Веревочные счеты с узелками употреблялись в России, а также во многих странах Европы. До сих пор еще практикуется завязывание узелков “на память”.

Новый способ записи чисел Однако с помощью черточек большие числа не запишешь, да и читать их трудно и долго. Около пяти тысяч лет назад почти одновременно в разных странах - Вавилонии, Египте, Китае - родился новый способ записи чисел: с помощью особых знаков - цифр.

Системы счисления

СИСТЕМЫ СЧИСЛЕНИЯ СИСТЕМЫ СЧИСЛЕНИЯ (нумерация) – совокупность способов обозначения натуральных чисел. На ранних ступенях развития общества люди почти не умели считать. Они различали совокупности двух и трех предметов; всякая совокупность, содержавшая большее число предметов, объединялась в понятие «много». Предметы при счете сопоставлялись обычно с пальцами рук и ног.

СИСТЕМЫ СЧИСЛЕНИЯ По мере развития цивилизации потребность человека в счете стала необходимой. Первоначально натуральные числа изображались с помощью некоторого количества черточек или палочек, затем для их изображения стали использовать буквы или специальные знаки.

ДВЕНАДЦАТЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ Широкое распространение имела в древности и двенадцатеричная система, происхождение которой, вероятно, связано, как и десятичной системы, со счетом на пальцах: за единицу счета принимались фаланги (отдельные суставы) четырех пальцев одной руки, которые при счете перебирались большим пальцем той же руки.

ПЯТЕРИЧНАЯ И ДВАДЦАТЕРИЧНАЯ СИСТЕМЫ СЧИСЛЕНИЯ У ряда африканских племен и в Древнем Китае была употребительна пятеричная система счисления. В Центральной Америке (у древних ацтеков и майя) и среди населявших Западную Европу древних кельтов была распространена двадцатеричная система.

СЛАВЯНСКАЯ СИСТЕМА НУМЕРАЦИИ В древнем Новгороде использовалась славянская система, где применялись буквы славянского алфавита; при изображении чисел над ними ставился знак ~ (титло).

СЛАВЯНСКАЯ СИСТЕМА НУМЕРАЦИИ В славянской системе нумерации для записи чисел использовались все буквы алфавита, правда, с некоторым нарушением алфавитного порядка. Различные буквы означали различное количество единиц, десятков и сотен. Например, число 231 записывалось в виде ~ СЛА (C – 200, Л – 30, А – 1).

РИМСКАЯ НУМЕРАЦИЯ Древние римляне пользовались нумерацией, сохраняющейся до настоящего времени под именем «римской нумерации», в которой числа изображаются буквами латинского алфавита. Сейчас ею пользуются для обозначения юбилейных дат, нумерации некоторых страниц книги (например, страниц предисловия), глав в книгах, строф в стихотворениях и т.д. В позднейшем своем виде римские цифры выглядят так:

РИМСКАЯ НУМЕРАЦИЯ Выполнение арифметических действий над многозначными числами в этой записи очень трудно. Тем не менее, римская нумерация преобладала в Италии до XIII в., а в других странах Западной Европы – до XVI в.

НЕДОСТАТКИ СЛАВЯНСКОЙ И РИМСКОЙ НУМЕРАЦИИ Этим системам свойственны два недостатка, которые привели к их вытеснению другими: необходимость большого числа различных знаков, особенно для изображения больших чисел; неудобство выполнения арифметических операций.

ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ Более удобной и общепринятой и наиболее распространенной является десятичная система счисления, которая была изобретена в Индии, заимствована там арабами и затем через некоторое время пришла в Европу. В десятичной системе счисления основанием является число 10. Индийцы первыми использовали ноль для указания позиционной значимости величины в строке цифр. Эта система получила название десятичной, так как в ней десять цифр.

ВАВИЛОНСКАЯ СИСТЕМА СЧИСЛЕНИЯ Существовали системы счисления и с другими основаниями. В Древнем Вавилоне, например, применялась шестидесятеричная система счисления. Остатки ее мы находим в сохранившемся до сих пор делении часа или градуса на 60 минут, а минуты – на 60 секунд.

ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ Самой молодой системой счисления по праву можно считать двоичную. Эта система обладает рядом качеств, делающей ее очень выгодной для использования в вычислительных машинах и в современных компьютерах.

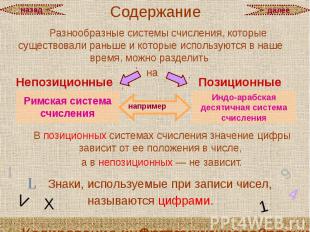
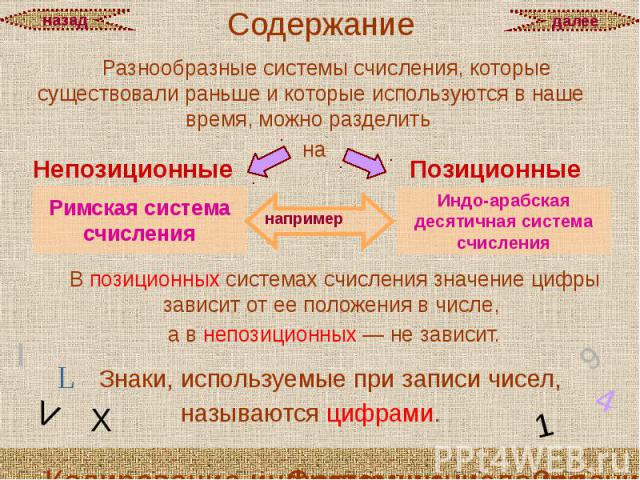
Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на

ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ

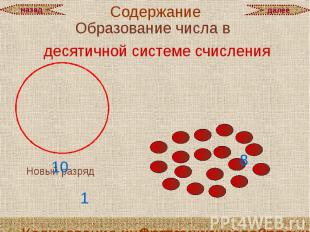
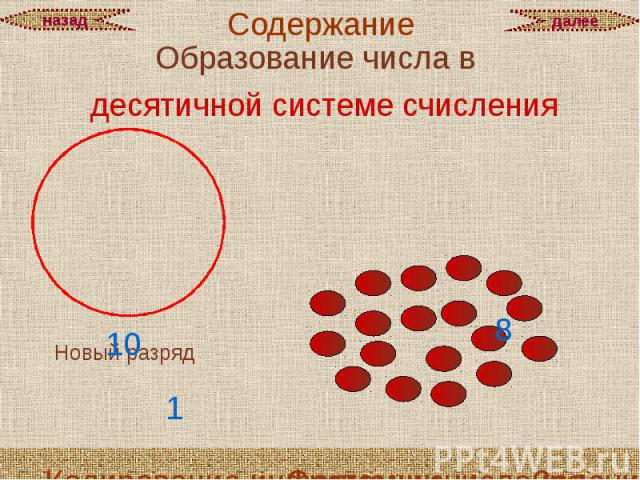
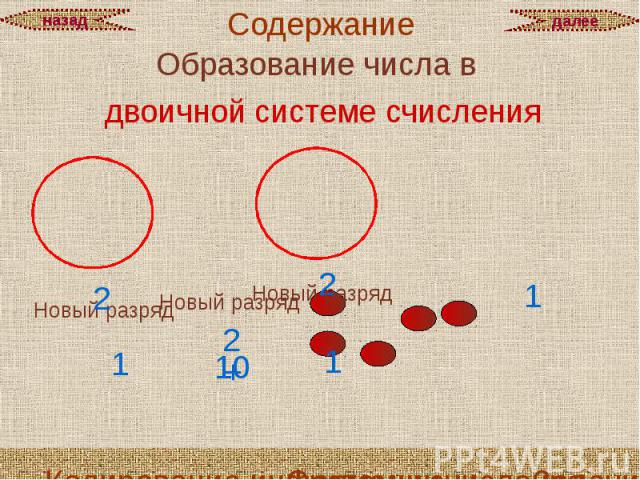
Образование числа в

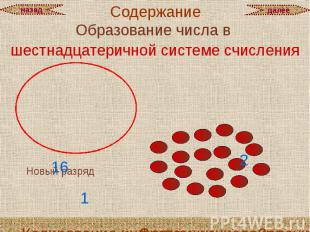
Образование числа в

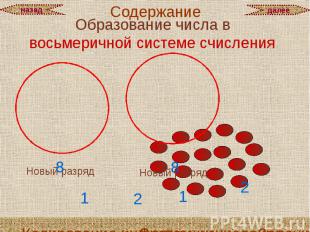
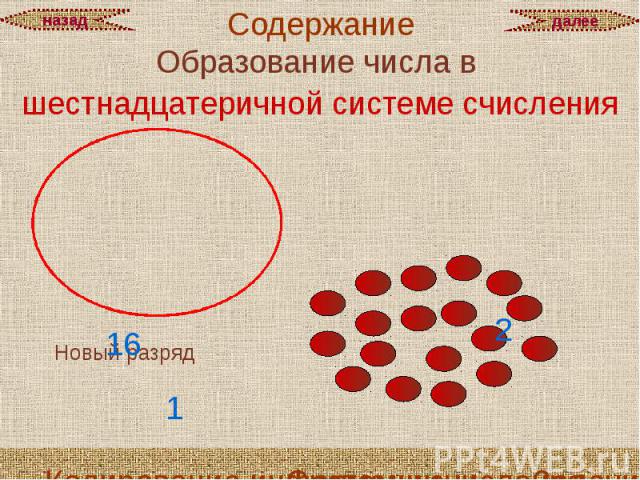
Образование числа в

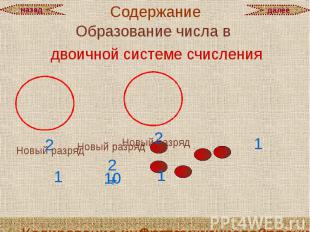
Образование числа в

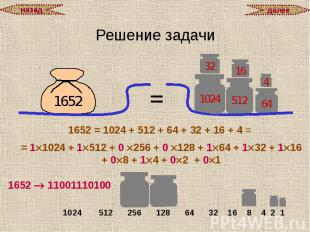
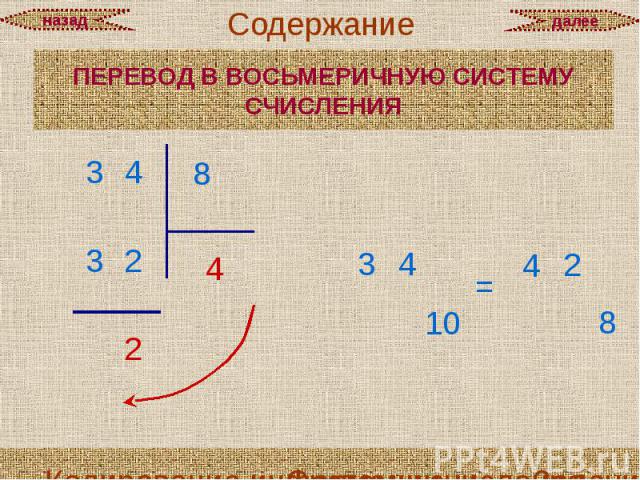
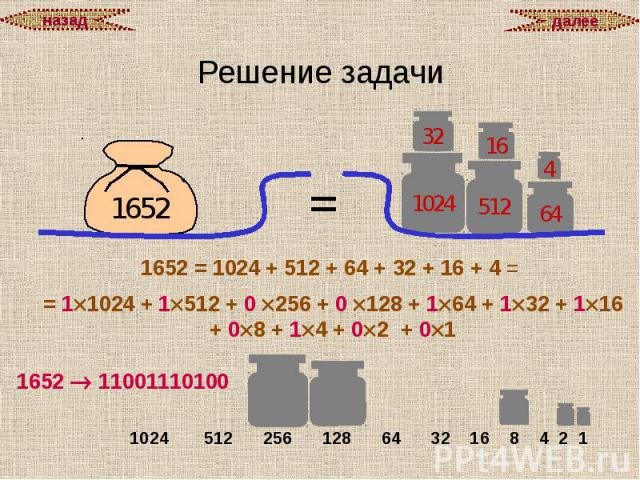
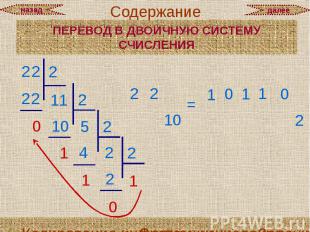
Перевод из десятичной системы счисления Общий прием перевода целых чисел из десятичной системы счисления в другую систему состоит в следующем: нужно разделить нацело данное число на основание новой системы счисления p (полученный от деления остаток будет младшим разрядом числа в новой системе), затем частное от деления нужно снова разделить на p (остаток от деления будет следующим разрядом числа в новой системе); такое последовательное деление необходимо продолжать до получения частного, которое будет меньше, чем p; это частное будет старшим разрядом числа в новой системе.

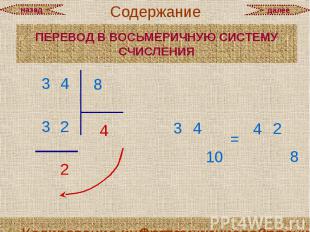
ПЕРЕВОД В ШЕСТНАДЦАТЕРИЧНУЮ СИСТЕМУ СЧИСЛЕНИЯ

Арифметические действия в двоичной системе счисления Арифметические действия, выполняемые в двоичной системе, подчиняются тем же правилам, что и в десятичной системе. Только в двоичной системе перенос единиц в старший разряд возникает чаще, чем в десятичной. Вот как выглядит таблица сложения в двоичной системе: 0 + 0 = 0, 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0 (перенос в старший разряд)

Арифметические действия в двоичной системе счисления Таблица умножения для двоичных чисел еще проще: 0 * 0 = 0, 0 * 1 = 0, 1 * 0 = 0, 1 * 1 = 1. Двоичное деление основано на методе, знакомом вам по десятичному делению, т. е. сводится к выполнению операций умножения и вычитания. Выполнение основной процедуры – выбор числа, кратного делителю и предназначенного для уменьшения делимого, здесь проще, так как таким числом могут быть только либо 0, либо сам делитель.

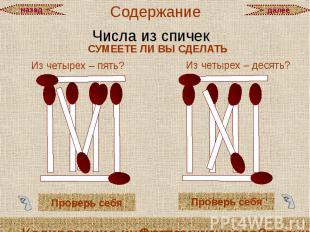
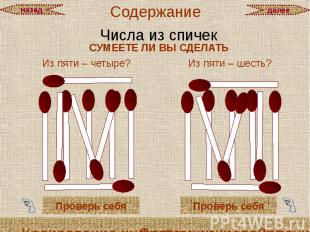
ЗАДАЧИ для самостоятельного решения