Презентация на тему: Свойства квадрата


Узнать, что такое удивительный квадрат и почему он удивительный. Узнать, что такое удивительный квадрат и почему он удивительный. Изучить замечательные свойства квадрата и почему они называются замечательными? Изучить стиль работы над задачами на разрезание квадрата. Изучить логику решения головоломок с квадратами.

подробнее исследовать свойства квадрата, подробнее исследовать свойства квадрата, рассмотреть геометрические способы раскроя квадрата, обосновать возможности превращений фигур при помощи разрезания квадрата, найти различные варианты построений, которые можно воспроизвести при помощи перегибания квадратного листа бумаги, и выявить преимущества в таком виде построений.

I. Введение I. Введение II. Основная часть: 1.Замечательные свойства квадрата 2. Квадрат в квадрате 3. Задачи на разрезание 4. Построения при помощи перегибания квадратного листа 5. Танграм III. Заключение.

В искусстве самым известным квадратом является «Черный квадрат» Казимира Малевича — символ русского авангарда! В искусстве самым известным квадратом является «Черный квадрат» Казимира Малевича — символ русского авангарда!

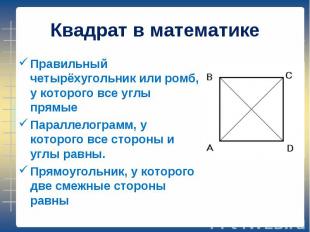
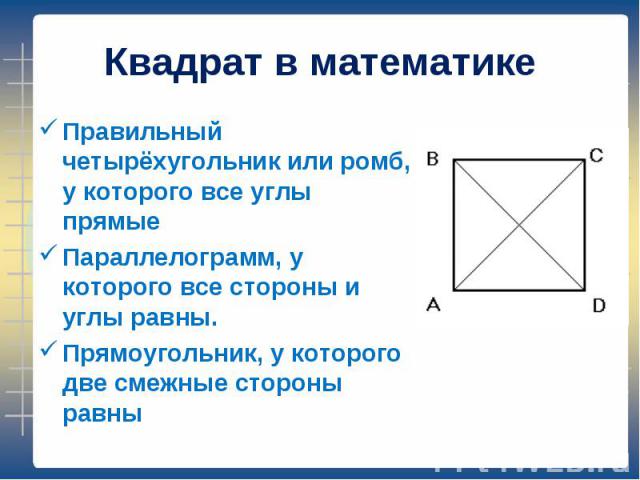
Правильный четырёхугольник или ромб, у которого все углы прямые Правильный четырёхугольник или ромб, у которого все углы прямые Параллелограмм, у которого все стороны и углы равны. Прямоугольник, у которого две смежные стороны равны
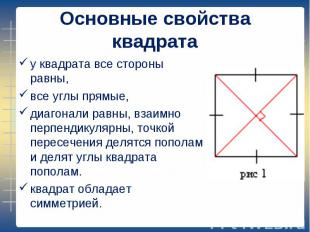
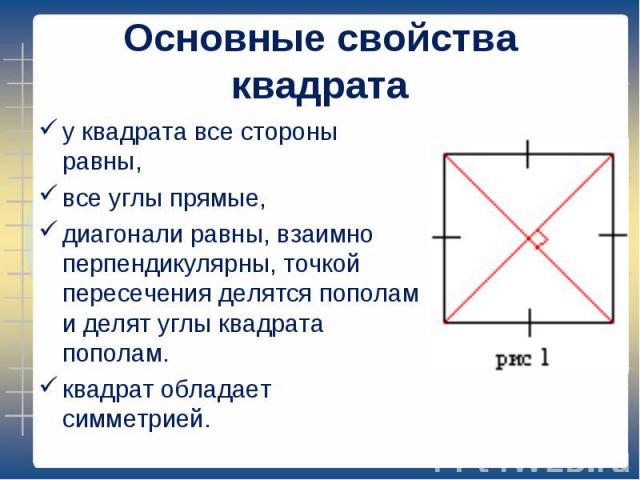
у квадрата все стороны равны, у квадрата все стороны равны, все углы прямые, диагонали равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам. квадрат обладает симметрией.
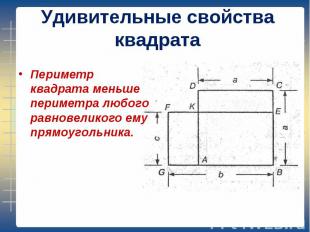
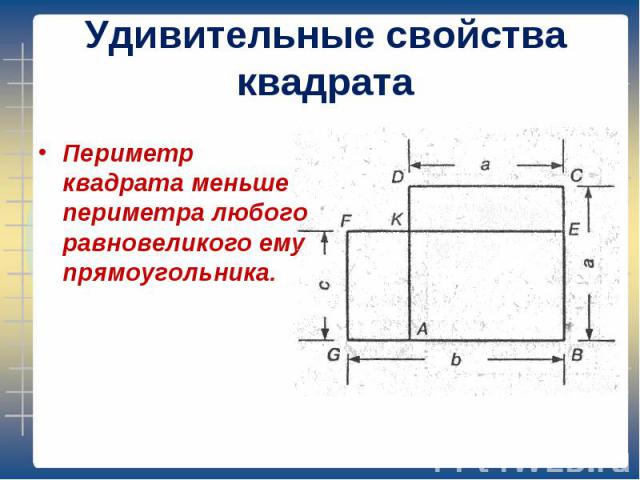
Периметр квадрата меньше периметра любого равновеликого ему прямоугольника. Периметр квадрата меньше периметра любого равновеликого ему прямоугольника.

Площадь квадрата больше площади любого прямоугольника с тем же периметром. Площадь квадрата больше площади любого прямоугольника с тем же периметром.

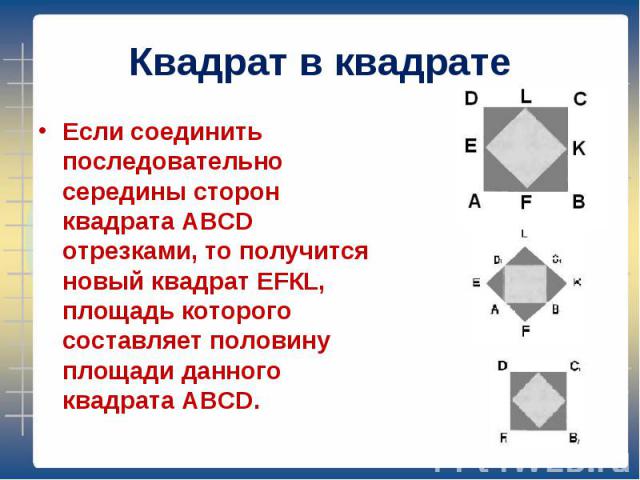
Если соединить последовательно середины сторон квадрата АВСD отрезками, то получится новый квадрат ЕFКL, площадь которого составляет половину площади данного квадрата АВСD. Если соединить последовательно середины сторон квадрата АВСD отрезками, то получится новый квадрат ЕFКL, площадь которого составляет половину площади данного квадрата АВСD.

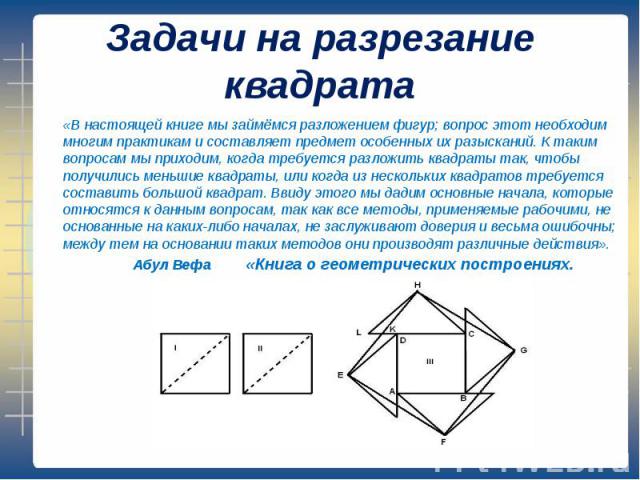
«В настоящей книге мы займёмся разложением фигур; вопрос этот необходим многим практикам и составляет предмет особенных их разысканий. К таким вопросам мы приходим, когда требуется разложить квадраты так, чтобы получились меньшие квадраты, или когда из нескольких квадратов требуется составить большой квадрат. Ввиду этого мы дадим основные начала, которые относятся к данным вопросам, так как все методы, применяемые рабочими, не основанные на каких-либо началах, не заслуживают доверия и весьма ошибочны; между тем на основании таких методов они производят различные действия». «В настоящей книге мы займёмся разложением фигур; вопрос этот необходим многим практикам и составляет предмет особенных их разысканий. К таким вопросам мы приходим, когда требуется разложить квадраты так, чтобы получились меньшие квадраты, или когда из нескольких квадратов требуется составить большой квадрат. Ввиду этого мы дадим основные начала, которые относятся к данным вопросам, так как все методы, применяемые рабочими, не основанные на каких-либо началах, не заслуживают доверия и весьма ошибочны; между тем на основании таких методов они производят различные действия». Абул Вефа

Искусство складывания из бумаги различных фигурок возникло в Японии в VII – VI в.в. хотя сама технология бумажного производства была разработана в Китае задолго до этого времени, ещё до нашей эры. Искусство складывания из бумаги различных фигурок возникло в Японии в VII – VI в.в. хотя сама технология бумажного производства была разработана в Китае задолго до этого времени, ещё до нашей эры. Развитие оригами как современного направления искусства связывают с именем знаменитого японского мастера Акиро Йошидзавы. Возможно, немаловажную роль в этом сыграло случайное совпадение звучания слов «бог» и «бумага» - по-японски «ками». Так возникла мистическая связь между религиозными ритуалами в синтоистских храмах и сложенными фигурками из бумаги («оригами»)

Если перегнуть бумажный квадрат пополам, чтобы одна сторона совпадала с противоположною ей. Получится сгиб, проходящий через центр квадрата. Если перегнуть бумажный квадрат пополам, чтобы одна сторона совпадала с противоположною ей. Получится сгиб, проходящий через центр квадрата. Линия этого сгиба обладает следующими свойствами: она перпендикулярна двум другим сторонам квадрата, делит эти стороны пополам, параллельно двум первым сторонам квадрата, сама делится в центре квадрата пополам, делит квадрат на два совпадающих при наложении прямоугольника, каждый из этих прямоугольников равновелик (т. е. равен по площади) одному из треугольников, на которые квадрат делиться диагональю.

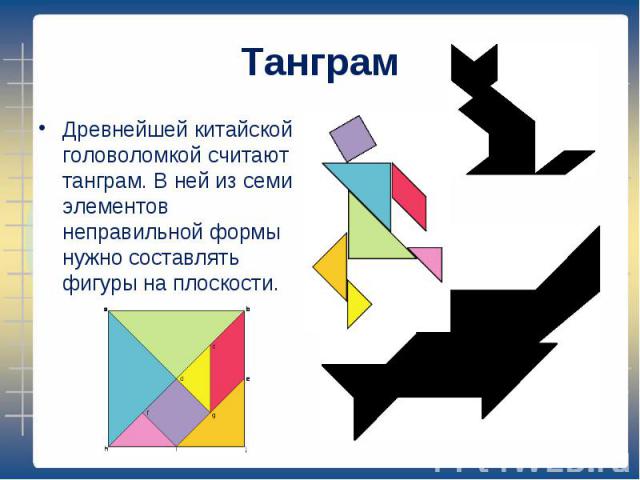
Древнейшей китайской головоломкой считают танграм. В ней из семи элементов неправильной формы нужно составлять фигуры на плоскости. Древнейшей китайской головоломкой считают танграм. В ней из семи элементов неправильной формы нужно составлять фигуры на плоскости.

периметр квадрата меньше периметра любого равновеликого ему прямоугольника; периметр квадрата меньше периметра любого равновеликого ему прямоугольника; площадь квадрата больше площади любого прямоугольника с тем же периметром; при помощи разрезаний можно произвести превращения различных многоугольников в квадрат. при помощи перегибания квадратного листа бумаги можно выполнять различные построения, не имея под рукой никаких инструментов – ни линейки, ни циркуля, ни даже карандаша; существуют занимательные игры, в которых используется квадрат: оригами, танграм.

Кордемский Б.А., Русалев Н.В. Удивительный квадрат. – М.: Столетие, 1994. Кордемский Б.А., Русалев Н.В. Удивительный квадрат. – М.: Столетие, 1994. Лоповок Л.М. Тысяча проблемных задач по математике: Книга для учащихся. – М.: Просвещение, 1995, с.38. Афонькин С.Ю., Афонькина Е.Ю. Весёлые уроки оригами в школе и дома: Учебник. – СПб.: Издательский дом «Литера», 2001. – 208 с.: ил. Белим С. Н. Задачи по геометрии, решаемые методами оригами. – М.: изд. «Аким», 1998г., 66с. Мартина Гарднера “Математические головоломки и развлечения” (М.:Мир, 1971).