Презентация на тему: Сложение и вычитание дробей с разными знаменателями

Суфийская притча «Делёж верблюдов» Суфийская притча «Делёж верблюдов» Живший некогда Суфий хотел сделать так, чтобы ученики после его смерти нашли подходящего им учителя Пути. Поэтому в завещании, после обязательного по закону раздела имущества, он оставил своим ученикам семнадцать верблюдов с таким указанием: «Разделите верблюдов между самым старшим, средним по возрасту и самым младшим из вас следующим образом: старшему пусть будет половина, среднему — треть, а младшему — одна девятая». Когда Суфий умер, и завещание было прочитано, ученики вначале были изумлены таким неумелым распределением имущества Мастера. Одни предлагали: «Давайте владеть верблюдами сообща»; другие искали совета и затем говорили: «Нам советовали разделить способом, наиболее близким к указанному»; третьим судья посоветовал продать верблюдов и поделить деньги; а ещё некоторые считали, что завещание утратило свою законную силу, поскольку его условия не могут быть выполнены. Спустя некоторое время ученики пришли к мысли, что в завещании Мастера мог быть какой-то скрытый смысл, и они стали расспрашивать повсюду о человеке, который может решать неразрешимые задачи. К кому бы они ни обращались, никто не мог помочь им, пока они не постучали в дверь Хазрата Али, зятя Пророка. Он сказал: — Вот вам решение. Я добавлю одного верблюда к этим семнадцати. Из восемнадцати верблюдов вы возьмете половину — девять верблюдов — для старшего ученика. Второй ученик возьмет треть — то есть шесть верблюдов. Третий получит одну девятую — двух верблюдов. Это как раз семнадцать. Остался один — мой верблюд, он вернётся ко мне.

О каких математических понятиях идет речь?

Актуализация знаний Устная работа: 1. сократите дроби: 2. Выделите целую часть: 3.Приведи дроби к НОЗ:

6. Вычислите 6. Вычислите

Тема урока: «Сложение и вычитание дробей с разными знаменателями» Цель урока: Учимся складывать и вычитать дроби с разными знаменателями.

Задание: дополнить известный алгоритм, чтобы можно было по нему выполнить сложение и вычитание дробей с разными знаменателям и показать на предложенных примерах, как он действует. У каждой мини- группы на столе таблички известного алгоритма. Задание: дополнить известный алгоритм, чтобы можно было по нему выполнить сложение и вычитание дробей с разными знаменателям и показать на предложенных примерах, как он действует. У каждой мини- группы на столе таблички известного алгоритма.

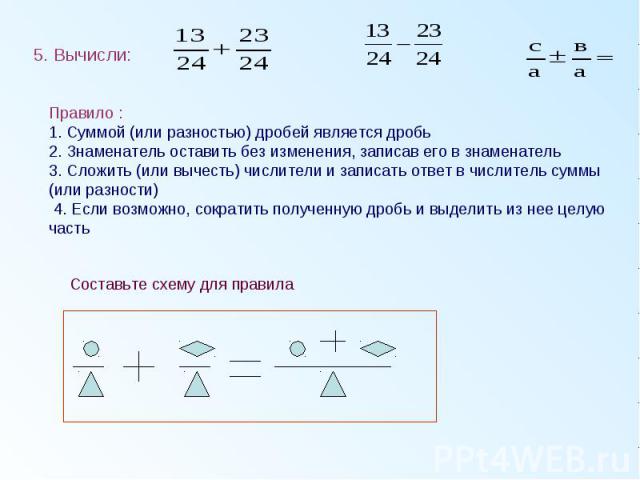
Результатом обсуждения является алгоритм сложения и вычитания дробей: 1.Суммой (или разностью) дробей является дробь 2.Найти НОЗ дробей 3. найти дополнительные множители (НОЗ делим на каждый знаменатель) 4.Найти новые числители действием умножением 5.Сложить (или вычесть) числители и записать ответ в числитель суммы (или разности) 6.Если возможно, сократить полученную дробь и выделить и нее целую часть 1 3 1. приведём дроби к наименьшему общему знаменателю, НОЗ (24,8)=24 2. дополнительный множитель для первой дроби равен 1, для второй дроби – 3. 3. складываем числители, знаменатель оставляем без изменения. Дробь сократимая, сокращаем.

В математике нельзя пропускать ни одного слова в некоторых правилах. ОЗ и НОЗ не всегда совпадают. В математике нельзя пропускать ни одного слова в некоторых правилах. ОЗ и НОЗ не всегда совпадают. Когда ещё не было электричества, мэр одного города любил вечером гулять по городским улицам. Как-то он столкнулся с одним горожанином, у него на лбу выскочила шишка. На следующий день он издал указ: “В тёмное время суток на улицу выходить с фонарём”. А вечером на него налетел тот же горожанин. Мэр потребовал у него фонарь. - Вот, - сказал прохожий. - А где свеча? – спросил мэр. - А в указе не написано, что в фонаре должна быть свеча, - ответил тот. Мэр издал второй указ: “В тёмное время суток на улицу выходить с фонарём со свечой”. В третий день история повторилась. Мэр уже вышел из себя. - Думаете, что ответил мэру прохожий? В приказе не написано, что свеча фонаря должна быть зажжена. Мэру пришлось издать указ третий раз, только после этого прохожий оставил его в покое. Поэтому наша задача – хорошо знать алгоритм и уметь его применять.

Задание: Задание: 1) а) б) 2) а) б)

Самостоятельная работа