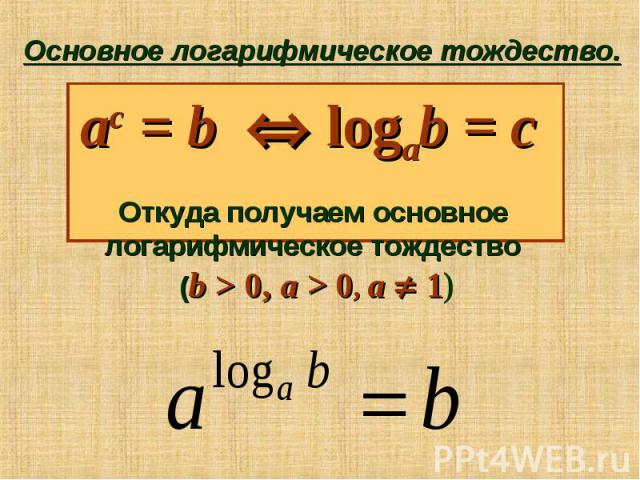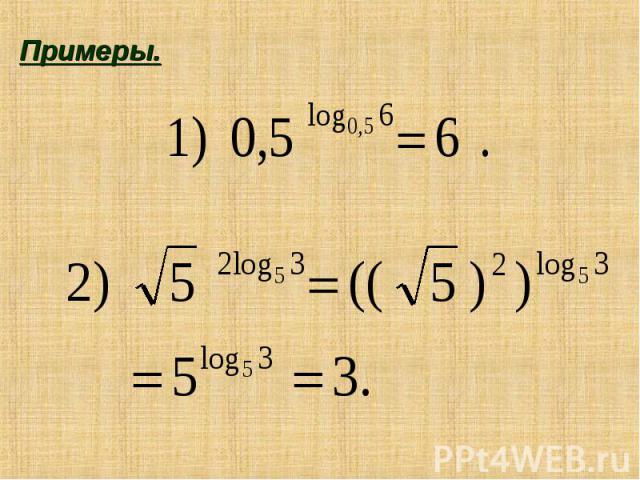Презентация на тему: Понятие логарифма, основные свойства логарифмов

Понятие логарифма, основные свойства логарифмов

Решите уравнение. Показатель степени – это и есть логарифм (при определенных условиях). 3) 4х+1+4х = 320 , 4х(4+1) = 320 , 4х = 64 , х = 3. Мы искали показатель степени, в который надо возвести основание 4, чтобы получить 64.

Определение. Логарифмом числа b (b > 0) по основанию a ( a > 0, a 1) называется показатель степени c, в которую нужно возвести основание a, чтобы получить число b , т.е. если ac = b , то можно записать logab = c .

log232, здесь b = 32, a = 2, c = 5. log232 = 5 , т. к. 25 = 32 . log50,04 , здесь b = 0,04, a = 5, c = - 2. log50,04 = - 2, т. к. 5-2 = 1/25 = 0,04 . 3) Найти х, такое, что log8х = 1/3. По определению логарифма х = 81/3 = 2.

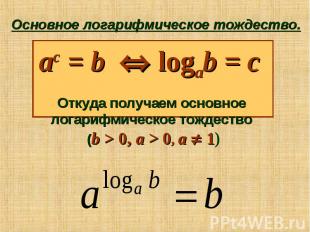
Основное логарифмическое тождество. ac = b logab = c Откуда получаем основное логарифмическое тождество (b > 0, a > 0, a 1)

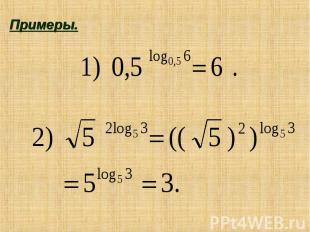
Примеры.

Свойства логарифмов.

Свойства логарифмов, примеры. Использовались свойства 4 , 5.1 и 2. Использовались свойства5.1, 3, 4 и 2.

Свойства логарифмов, примеры. Использовались свойства 4 , 5.1 и 2. Использовались свойства5.1, 3, 4 и 2.

Формула перехода от одного основания логарифма к другому, примеры.

Домашнее задание. 1) Разобрать и выучить лекцию.2) Никольский, 10 кл., п.5.1, 5.2 № 5.4, 5.8( а, б, в, е, и), 5.9(1,2 стр.)

Свойства логарифмов.