Презентация на тему: Логические законы

Логические законы

Закон тождестваЗакон непротиворечияЗакон исключенного третьегоЗакон двойного отрицанияЗаконы общей инверсии (законы де Моргана)Закон коммутативностиЗакон ассоциативностиЗакон дистрибутивностиЗакон идемпотентности (равносильности)Законы исключения константЗаконы поглощенияЗаконы исключения (склеивания)Закон контрапозиции (правило перевертывания)Выразить импликацию через конъюнкциюВыразить эквивалентность через базовые логические операции

Закон тождества Всякое высказывание тождественно самому себе А = А

Закон непротиворечия Высказывание не может быть одновременно истинным и ложным

Закон исключенного третьего Высказывание может быть либо истинным, либо ложным, третьего не дано.

Закон двойного отрицания Если дважды отрицать некоторое высказывание, то в результате получим исходное высказывание.

Законы общей инверсии (законы де Моргана) Для логического сложения Для логического умножения

Закон коммутативности (переместительный) Для логического сложения Для логического умножения

Закон ассоциативности (сочетательный) Если в логическом выражении используется только операция логического сложения или логического умножения, то можно пренебрегать скобками или расставлять их произвольно: Для логического сложения Для логического умножения

Закон дистрибутивности (распределительный) В алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые. Дистрибутивность сложения относительно умножения Дистрибутивность умножения относительно сложения

В обычной алгебре справедлив распределительный закон только для сложения: (A+B)C=AC+BC

Закон идемпотентности (равносильности) Для логического сложения Для логического умножения

Законы исключения констант Для логического умножения Для логического сложения

Законы поглощения Для логического сложения Для логического умножения

Законы исключения (склеивания) Для логического сложения Для логического умножения

Закон контрапозиции (правило перевертывания)

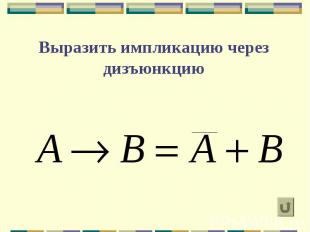
Выразить импликацию через дизъюнкцию

Выразить эквивалентность через базовые логические операции