Презентация на тему: Движения в пространстве

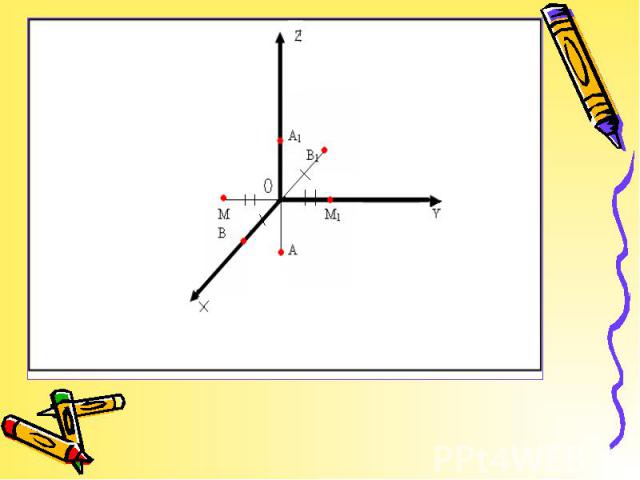
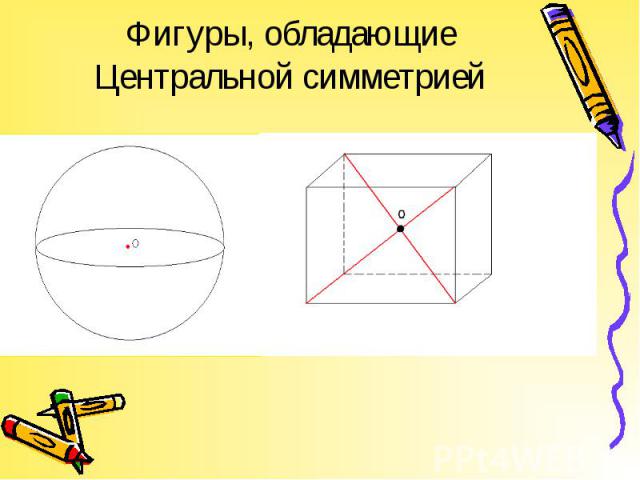
Центральная симметрия – отображение пространства на себе, при котором любая точка М переходит в симметричную ей точку М1 относительно данного центра О. Центральная симметрия – отображение пространства на себе, при котором любая точка М переходит в симметричную ей точку М1 относительно данного центра О.

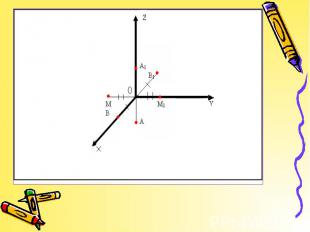
Осевой симметрией с осью а называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М1 относительно оси а. Осевой симметрией с осью а называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М1 относительно оси а. Осевая симметрия – это движение.

Рассмотрим теперь любые две точки A(x1; y1; z1) и B(x2;y2;z2) и докажем, что расстояние между симметричными им точками A1 и B1 равно AB. Точки A1 и B1 имеют координаты A1(-x1;-y1;-z1) и B1(-x1;-y1;-z1) По формуле расстояния между двумя точками находим: AB=\/(x2-x1)²+(y2-y1)²+(z2-z1), Рассмотрим теперь любые две точки A(x1; y1; z1) и B(x2;y2;z2) и докажем, что расстояние между симметричными им точками A1 и B1 равно AB. Точки A1 и B1 имеют координаты A1(-x1;-y1;-z1) и B1(-x1;-y1;-z1) По формуле расстояния между двумя точками находим: AB=\/(x2-x1)²+(y2-y1)²+(z2-z1), A1B1=\/(-x2+x1)²+(-y2+y1)²+(-z2+z1). Из этих соотношений ясно, что AB=A1B1, что и требовалось доказать.

Осевая симметрия встречается очень часто. Ее можно увидеть как в природе: листья растений или цветы, тело животных насекомых и даже человека, так и в творении самого человека: здания, автомобили, техника и многое другое. Осевая симметрия встречается очень часто. Ее можно увидеть как в природе: листья растений или цветы, тело животных насекомых и даже человека, так и в творении самого человека: здания, автомобили, техника и многое другое.

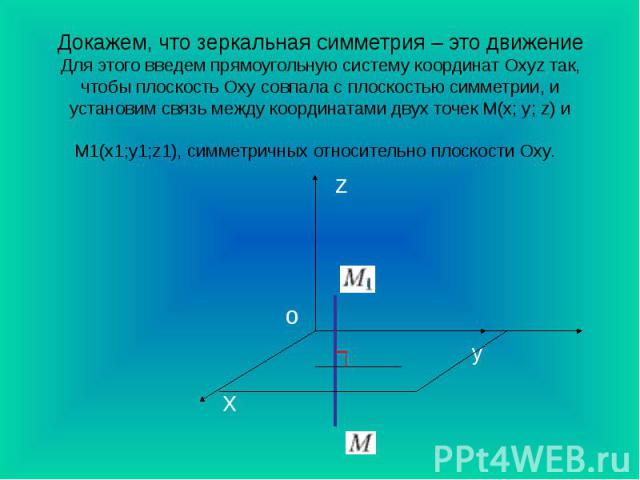
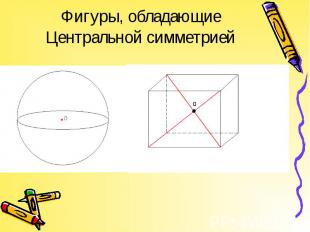
Отображение объемной фигуры, при котором каждой ее точке соответствует точка, симметричная ей относительно данной плоскости, называется отражением объемной фигуры в этой плоскости (или зеркальной симметрией). Отображение объемной фигуры, при котором каждой ее точке соответствует точка, симметричная ей относительно данной плоскости, называется отражением объемной фигуры в этой плоскости (или зеркальной симметрией).

Теорема 1. Отражение в плоскости сохраняет расстояния и, стало быть, является движением. Теорема 2. Движение, при котором все точки некоторой плоскости неподвижны, является отражением в этой плоскости или тождественным отображением. Зеркальная симметрия задается указанием одной пары соответствующих точек, не лежащих в плоскости симметрии: плоскость симметрии проходит через середину отрезка, соединяющего эти точки, перпендикулярно к нему. Теорема 1. Отражение в плоскости сохраняет расстояния и, стало быть, является движением. Теорема 2. Движение, при котором все точки некоторой плоскости неподвижны, является отражением в этой плоскости или тождественным отображением. Зеркальная симметрия задается указанием одной пары соответствующих точек, не лежащих в плоскости симметрии: плоскость симметрии проходит через середину отрезка, соединяющего эти точки, перпендикулярно к нему.

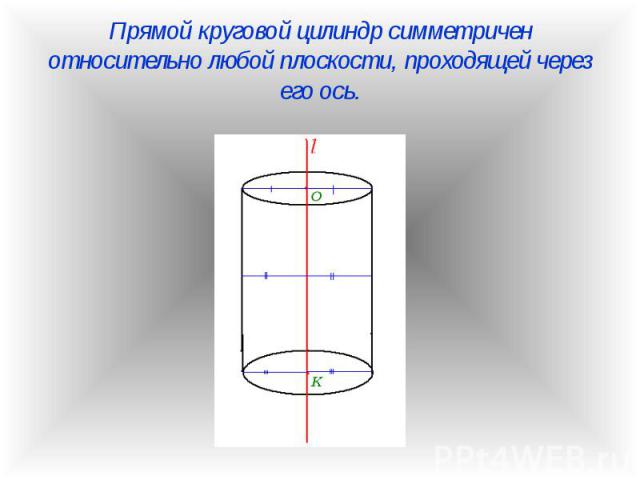
Симметрия относительно плоскости (зеркальная симметрия) пространства есть движение, а значит, обладает всеми свойствами движений: переводит прямую в прямую, плоскость --- в плоскость. Симметрия относительно плоскости (зеркальная симметрия) пространства есть движение, а значит, обладает всеми свойствами движений: переводит прямую в прямую, плоскость --- в плоскость. Кроме того, это преобразование пространства, совпадающее со своим обратным: композиция двух симметрий относительно одной и той же плоскости есть тождественное преобразование. При симметрии относительно плоскости все точки этой плоскости, и только они, остаются на месте (неподвижные точки преобразования). Прямые, лежащие в плоскости симметрии и перпендикулярные ей, переходят в себя. Плоскости, перпендикулярные плоскости симметрии также переходят в себя. Симметрия относительно плоскости является движением второго рода (меняет ориентацию тетраэдра).

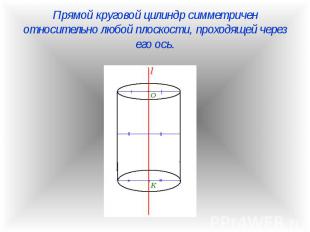
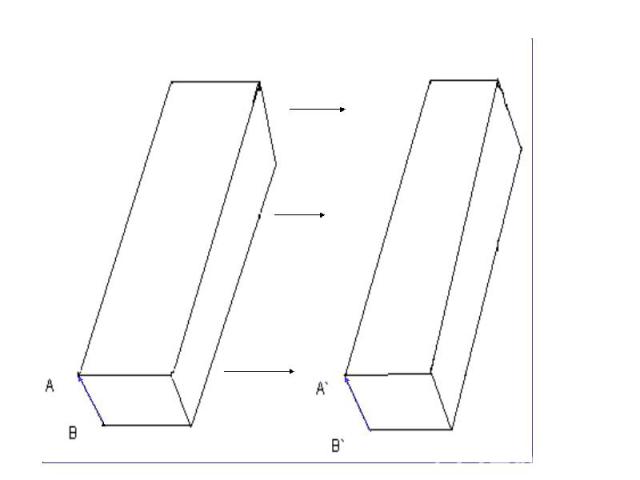
Движение плоскости – это взаимно однозначное преобразование точек плоскости при котором сохраняются расстояния: если точка А переходит в А`, В – В`, то А`В`=АВ Движение плоскости – это взаимно однозначное преобразование точек плоскости при котором сохраняются расстояния: если точка А переходит в А`, В – В`, то А`В`=АВ При движении так же сохраняются углы Параллельный перенос – это отображение пространства на себя, при котором любая точка М переходит в точку М’, что MM’ = р

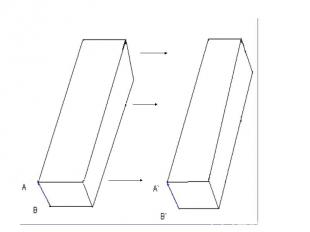
Мы так же можем увидеть «параллельный перенос в повседневной жизни. Мы видим эти мелочи повсюду, но вряд ли кто-то из нас задумывался об этом. Дизайн в квартирах иногда выполняют в стиле «параллели». Мы так же можем увидеть «параллельный перенос в повседневной жизни. Мы видим эти мелочи повсюду, но вряд ли кто-то из нас задумывался об этом. Дизайн в квартирах иногда выполняют в стиле «параллели».

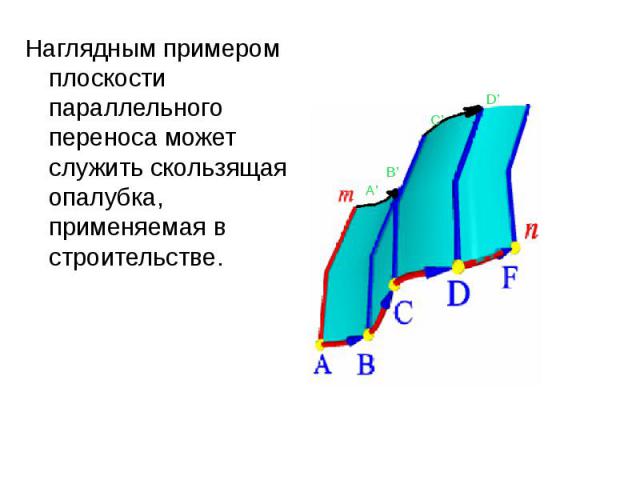
Поверхностью параллельного переноса называется поверхность, образованная поступательным плоскопараллельным перемещением образующей - плоской кривой линии m по криволинейной направляющей n Поверхностью параллельного переноса называется поверхность, образованная поступательным плоскопараллельным перемещением образующей - плоской кривой линии m по криволинейной направляющей n

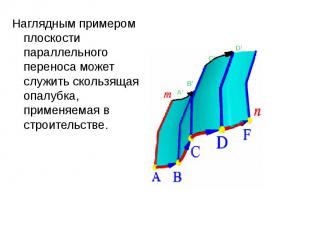
Наглядным примером плоскости параллельного переноса может служить скользящая опалубка, применяемая в строительстве. Наглядным примером плоскости параллельного переноса может служить скользящая опалубка, применяемая в строительстве.