Презентация на тему: Алгоритм решения задач по теме «Законы сохранения»

Алгоритм решения задач по теме «Законы сохранения» 1) Внимательно изучите условие задачи, поймите физическую сущность явлений и процессов, рассматриваемых в задаче, уясните основной вопрос задачи. 2) Мысленно представьте ситуацию, описанную в задаче, выясните цель решения, четко выделите данные и неизвестные величины. 3) Запишите краткое условие задачи. Одновременно выразите все величины в единицах СИ. 4) Сделайте чертеж, на котором отобразите ситуацию до и после события. 5) Запишите закон сохранения импульса (в проекции на выбранную ось) проверив систему на замкнутость или (и) закон сохранения энергии в соответствии с тем, что отобразили на чертеже (с одной стороны равенства что было «до», с другой что «после»). Выберите нулевой уровень потенциальной энергии. 6) Решите уравнение или систему уравнений относительно неизвестной величины, т.е. решите задачу в общем виде. 7) Если не все величины известны, то для нахождения их можете применить алгоритм решения задач по теме «Динамика». 8) Найдите искомую величину. 9) Определите единицу величины. Проверьте, подходит ли она по смыслу.10) Рассчитайте число.11) Проверьте ответ на «глупость» и запишите его.
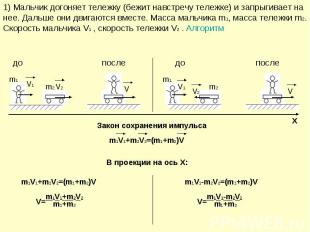
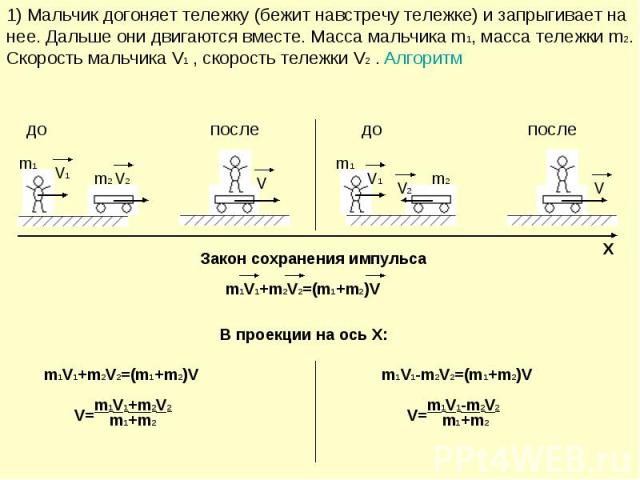
1) Мальчик догоняет тележку (бежит навстречу тележке) и запрыгивает на нее. Дальше они двигаются вместе. Масса мальчика m1, масса тележки m2. Скорость мальчика V1 , скорость тележки V2 . Алгоритм

2) На вагонетку массой 800 кг, катящуюся по горизонтальному пути со скоростью 0,2 м/с, насыпали сверху 200 кг щебня. На сколько уменьшилась скорость вагонетки? Алгоритм

3) Рыбак массой 60 кг переходит с носа на корму лодки. На сколько переместится лодка длиной 3 м и массой 120 кг относительно воды? алгоритм

4) Охотник стреляет с легкой надувной лодки. Какую скорость приобретает лодка в момент выстрела, если масса охотника с лодкой равна 70 кг, масса дроби 35 г и средняя начальная скорость дроби 320 м/с? Ствол ружья во время выстрела образует угол 60° к горизонту. алгоритм

5) Граната, летевшая в горизонтальном направлении со скоростью 10 м/с, разорвалась на два осколка массами 1 кг и 1,5 кг. Скорость большого осколка после разрыва горизонтально возросла до 25 м/с. Определите скорость и направление движения меньшего осколка. алгоритм

6) Пуля летит горизонтально со скоростью 400м/с пробивает стоящий на горизонтальной шероховатой поверхности коробку и продолжает движение в прежнем направлении со скоростью ¾ V0. Масса коробки в 40 раз больше массы пули. Коэффициент трения скольжения между коробкой и поверхностью М= 0,15. На какое расстояние переместилась коробка к моменту, когда ее скорость уменьшится на 20%. Алгоритм Динамика (ЕГЭ)

7) Тело массой 3 кг, свободно падает с высоты 5 м. Найти потенциальную и кинетическую энергию тела на расстоянии 2 м от поверхности земли. алгоритм

8) Камень подброшен вертикально вверх с начальной скоростью 10 м/с. На какой высоте h кинетическая энергия камня равна его потенциальной энергии? алгоритм

9) Груз массой 25 кг висит на шнуре длиной 2,5 м. На какую наибольшую высоту можно отвести в сторону груз, чтобы при дальнейших свободных качаниях шнур не оборвался? Максимальная сила натяжения, которую выдерживает шнур не обрываясь, равна 550 Н. алгоритмПо закону сохранения энергии при переходе из точки 1 в точку 2 Значит, необходимо найти скорость в т. 2

10) Цирковой артист массой 60 кг падает в натянутую сетку с высоты 4 м. С какой силой действует на артиста сетка, если она прогибается при этом на 1 м? алгоритм

11) Маятник массой m отклонен на угол α от вертикали. Какова сила натяжения нити при прохождении маятником положения равновесия? алгоритм
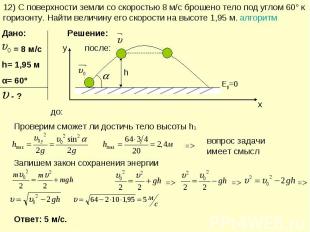
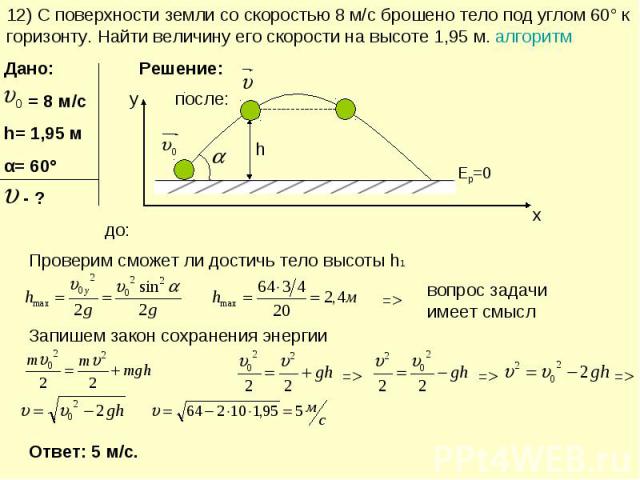
12) С поверхности земли со скоростью 8 м/с брошено тело под углом 60° к горизонту. Найти величину его скорости на высоте 1,95 м. алгоритм
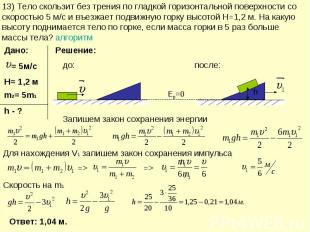
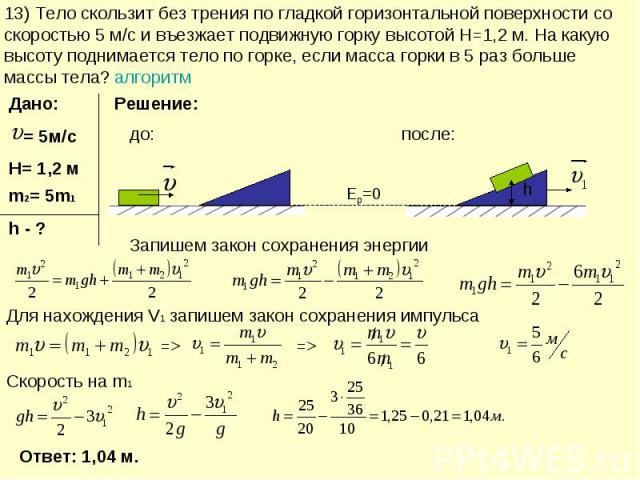
13) Тело скользит без трения по гладкой горизонтальной поверхности со скоростью 5 м/с и въезжает подвижную горку высотой H=1,2 м. На какую высоту поднимается тело по горке, если масса горки в 5 раз больше массы тела? алгоритм

14) Два тела массой по 1/18 кг движутся навстречу друг другу. Скорость первого тела 4 м/с, второго - 8 м/с. Какое количество теплоты выделится в результате абсолютно неупругого удара тел? алгоритм По закону сохранения энергии выделившееся количество тепла равно убыли механической (в нашем случае кинетической энергии)Найдем конечную скорость из закона сохранения импульса

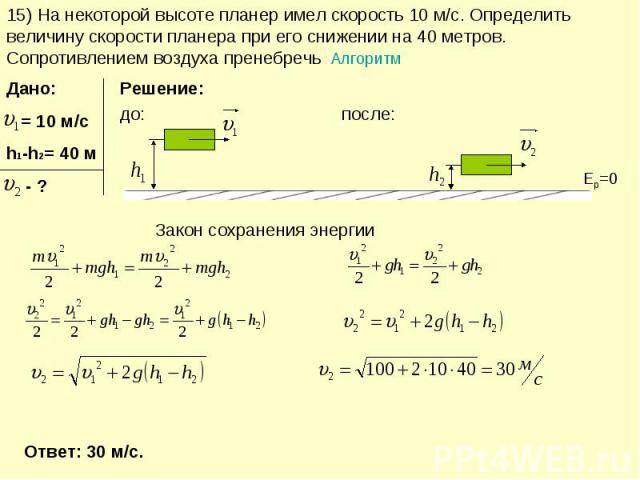
15) На некоторой высоте планер имел скорость 10 м/с. Определить величину скорости планера при его снижении на 40 метров. Сопротивлением воздуха пренебречь Алгоритм

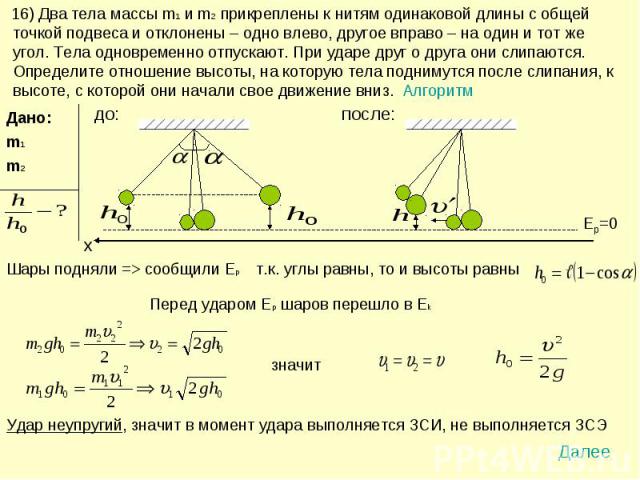
16) Два тела массы m1 и m2 прикреплены к нитям одинаковой длины с общей точкой подвеса и отклонены – одно влево, другое вправо – на один и тот же угол. Тела одновременно отпускают. При ударе друг о друга они слипаются. Определите отношение высоты, на которую тела поднимутся после слипания, к высоте, с которой они начали свое движение вниз. Алгоритм

Закон сохранения импульса в проекции на OX:В момент подъема шаров выполняется ЗСЭ
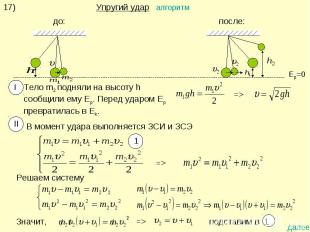
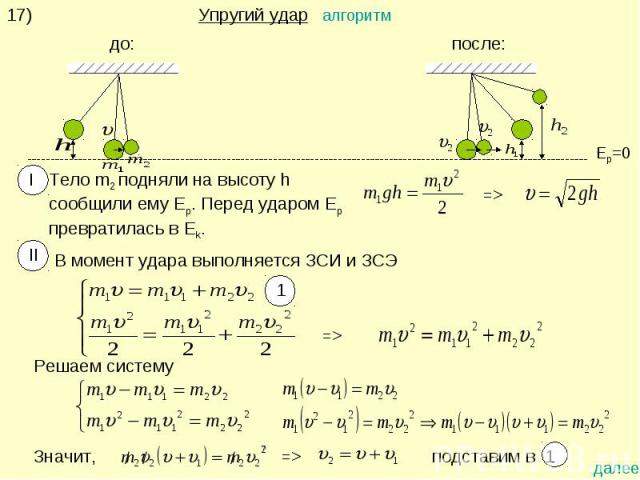
17)Упругий удар алгоритмТело m2 подняли на высоту h сообщили ему Ep. Перед ударом Ep превратилась в Ek.В момент удара выполняется ЗСИ и ЗСЭ

После удара шары поднимаются на высоту h1 и h2 . Выполняется ЗСЭ

18) Тяжелый шарик соскальзывает без трения по наклонному желобу, образующему «мертвую петлю» радиусом R. С какой высоты шарик должен начать движение, чтобы не оторваться от желоба в верхней точке траектории? Алгоритм Для нахождения V в точке 2 запишем II закон Ньютона

19) Два упругих шарика подвешены на тонких нитях рядом так, что они находятся на одной высоте и соприкасаются. Массы шариков m1 = 10г и m2 = 15г. Шарик массой m1 отклонился на угол α= 60°. Определить, каким должно быть отношение длины нитей , чтобы второй маятник отклонился на больший угол. Соударение считать абсолютно упругим. Алгоритм (Олимпиада)Разделим задачу на 3 этапа:I Отклоним шарик массой m1 II В момент удара выполняется ЗСЭ и ЗСИ

Решим системуIII Подъемы шаров после удара

20) К динамометру прикреплена невесомая пружина жесткостью k= 100 Н/м, на которой висит неподвижная невесомая чаша. На чашу с высоты h= 20 см падает кусок пластилина с нулевой начальной скоростью. Пластилин прилипает к чаше, при этом максимальное показание динамометра F= 5 Н. Чему равна масса пластилина. Алгоритм (ЕГЭ)
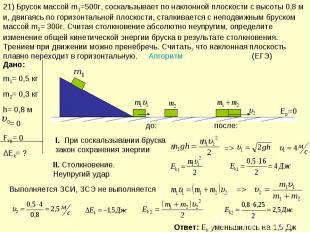
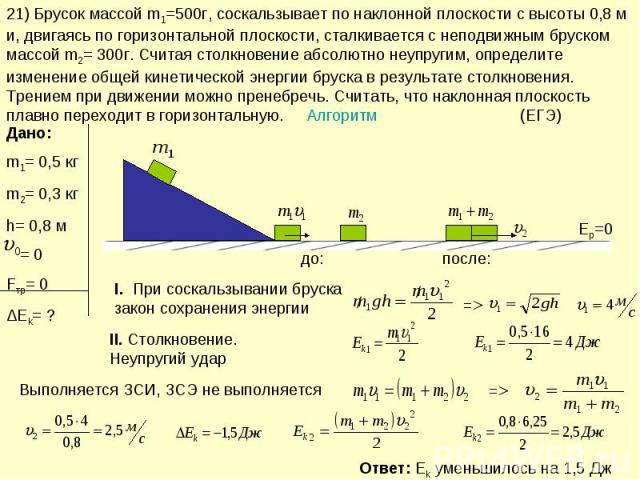
21) Брусок массой m1=500г, соскальзывает по наклонной плоскости с высоты 0,8 м и, двигаясь по горизонтальной плоскости, сталкивается с неподвижным бруском массой m2= 300г. Считая столкновение абсолютно неупругим, определите изменение общей кинетической энергии бруска в результате столкновения. Трением при движении можно пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную. Алгоритм (ЕГЭ) I. При соскальзывании бруска закон сохранения энергииII. Столкновение. Неупругий ударВыполняется ЗСИ, ЗСЭ не выполняется

22) Шар, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол 60° и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля, летящая на встречу шару со скоростью 300 м/с, которая пробивает шар и вылетает горизонтально со скоростью 200 м/с, после чего шар продолжает движение в прежнем направлении и отклоняется на угол 39°. Определите отношение масс шара и пули (Массу шара считать неизменной, диаметр шара – пренебрежительно малым, по сравнению с длиной нити, cos 39°= 7/9 ) Алгоритм (ЕГЭ)Разобьем задачу на 3 этапа:I. Шар из состояния I в состояние II. Закон сохранения энергии:

II. Момент удара:Выполняется ЗСИ, не выполняется ЗСЭIII. Шар поднимается и отклоняется на угол 39°

23) На гладком горизонтальном столе лежит шар массой М=240 г, прикрепленный к пружине жесткостью k=40 кН/м. Другой конец пружины закреплен. В шар попадает пуля массой m=10 г, имеющая в момент удара начальная скорость 400 м/с, направленную вдоль оси пружины. Пуля застревает в шаре. Определите амплитуду колебаний шара после удара. Алгоритм I. Момент удараII. При движении шара его Ek превращается в момент полного сжатия пружины в Ep

24) Начальная скорость снаряда, выпущенного вертикально вверх, равна 160 м/с. В точке максимального подъема снаряд разорвался на 2 осколка, массы которых относятся как 1:4. Осколки разлетелись в вертикальных направлениях, причем меньший осколок полетел вниз и упал на землю со скоростью 200 м/с. Определите скорость, которую имел в момент удара о землю больший осколок. Сопротивлением воздуха пренебречь. Алгоритм(ЕГЭ)I. Снаряд летит вверхII. Момент разрыва снаряда

III. Для второго осколка (без сопротивления ветра)

Алгоритм решения задач «Динамика»Сделайте чертеж. Изобразите тело, все действующие на него силы, покажите направление ускорения, выберите оси.Запишите второй закон Ньютона в векторном виде.Спроецируйте вектора полученного уравнения на оси и получите скалярные уравнения.Решите уравнение (систему уравнений) относительно искомой величины.