Презентация на тему: Принципы работы современных устройств навигации. Решение задачи о кратчайшем пути

Принципы работы современных устройств навигации.Решение задачи о кратчайшем путиУрок разработала учитель информатики МОБУ Лицея № 95Мусаева Н.Г.

Развитие познавательных интересов; Формирование у учащихся интереса к современным информационным устройствам, изучение принципа работы GPS-навигатора; Изучение нового материала, расширение знаний в области MS Excel;Построение и решение задачи о кратчайшем пути в графе методом линейного программирования;Воспитание информационной культуры учащихся, расширение знаний в области информационных технологий;Расширение знаний по теме, использование материала ЕГЭ.

1. С древнейших времен, человечество старается найти ответы на два вопроса: «Где Я?» и «Куда мы идем?». Для того, что бы ответить на эти вопросы мы, люди, придумали массу способов ориентирования. Какие?2. Зачем понадобились человечеству спутники и как они работают?3. Что такое навигатор и каков принцип его работы?4. Как можно определить кратчайший путь из одного пункта в другой?

Карта урока:

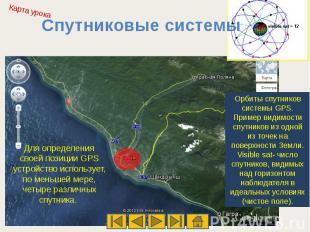
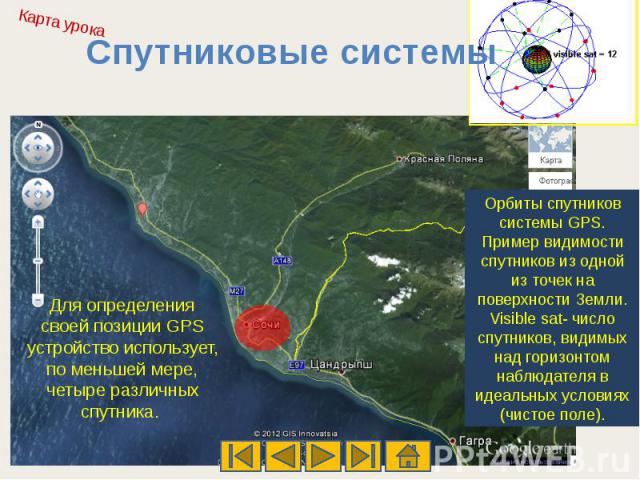
Спутниковые системыДля определения своей позиции GPS устройство использует, по меньшей мере, четыре различных спутника. Орбиты спутников системы GPS. Пример видимости спутников из одной из точек на поверхности Земли. Visible sat- число спутников, видимых над горизонтом наблюдателя в идеальных условиях (чистое поле).

Российские системы навигации

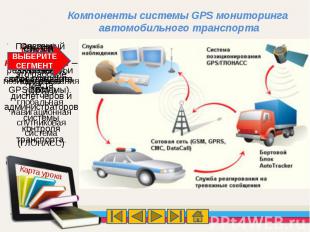
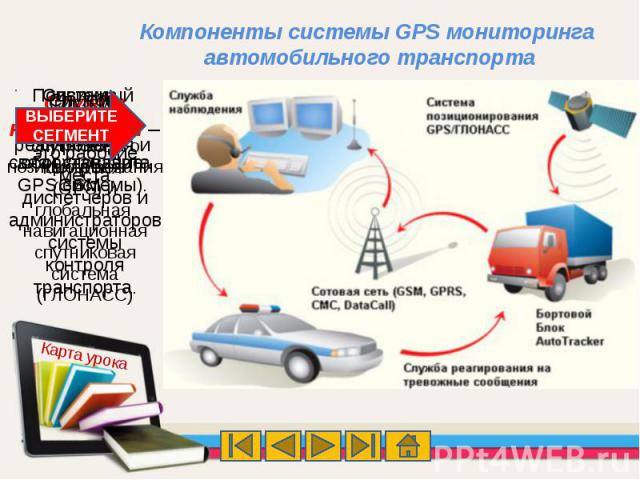
Компоненты системы GPS мониторинга автомобильного транспорта

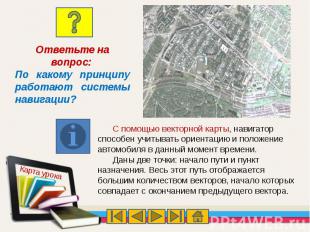
Ответьте на вопрос: По какому принципу работают системы навигации?С помощью векторной карты, навигатор способен учитывать ориентацию и положение автомобиля в данный момент времени.Даны две точки: начало пути и пункт назначения. Весь этот путь отображается большим количеством векторов, начало которых совпадает с окончанием предыдущего вектора.

Портативные навигаторы – отличаются малыми габаритами и легким весом. Используются как водителями автомобилей, так и туристами и всеми, кто совершает походы или прогулки, проходит незнакомыми маршрутами.

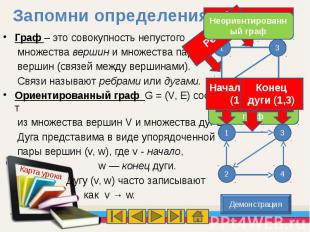
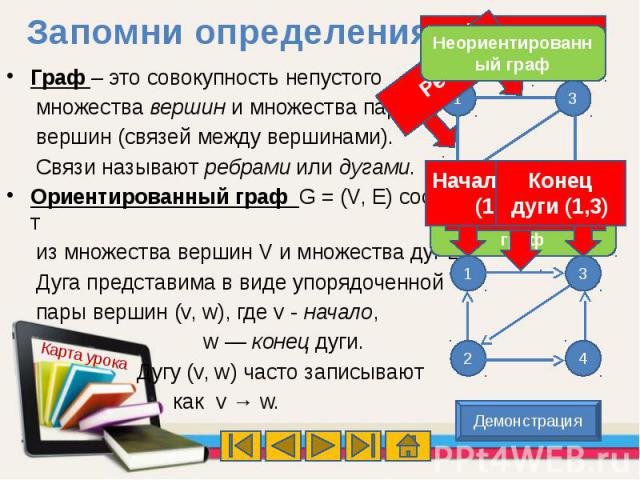
Граф – это совокупность непустого множества вершин и множества пар вершин (связей между вершинами). Связи называют ребрами или дугами.Ориентированный граф G = (V, Е) состоит из множества вершин V и множества дуг Е. Дуга представима в виде упорядоченной пары вершин (v, w), где v - начало, w — конец дуги. Дугу (v, w) часто записывают как v → w.

алгоритм на графах, изобретённый нидерландским ученым Эдсгером Вибе Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Каждой вершине из множества V сопоставим метку — минимальное известное расстояние от этой вершины до вершины а. Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.

+ Алгоритм Дейкстры используется для определения оптимального пути между двумя графами на карте. Навигатор, при введении начальной и конечной точки маршрута изучает расположение и длины граф, реорганизует все графы воедино и пытается определить все объекты, которые наиболее приближены к точке назначения. Единственный минус такого алгоритма состоит в том, что он не учитывает важности того или иного объекта, он считает, что все точки интереса одинаково важны, а ведь на самом деле, чем ближе объект к цели, тем он важнее или то, что по грунтовой дороге ехать труднее, чем по асфальтной трассе.

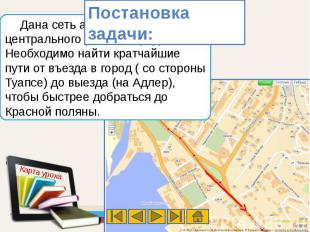
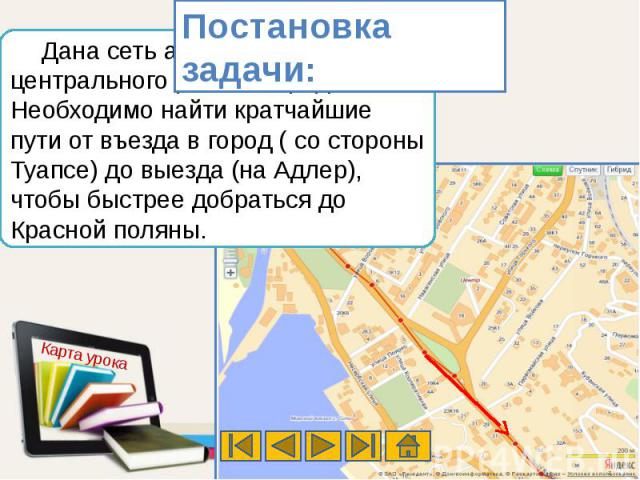
Дана сеть автомобильных дорог центрального района города Сочи. Необходимо найти кратчайшие пути от въезда в город ( со стороны Туапсе) до выезда (на Адлер), чтобы быстрее добраться до Красной поляны.

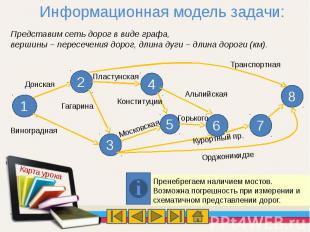
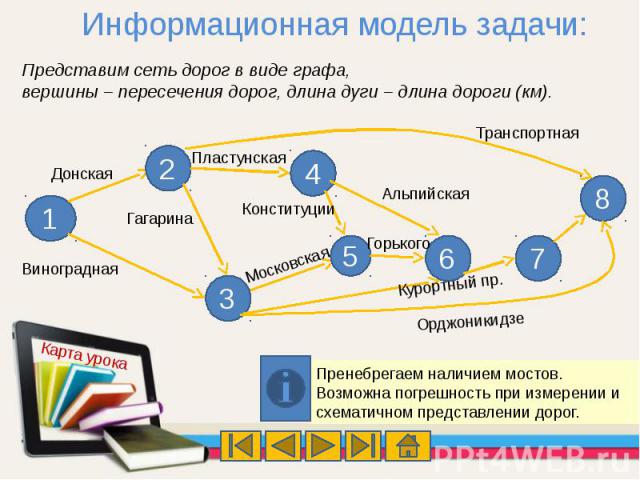
Информационная модель задачи:Представим сеть дорог в виде графа, вершины – пересечения дорог, длина дуги – длина дороги (км). Пренебрегаем наличием мостов.Возможна погрешность при измерении и схематичном представлении дорог.

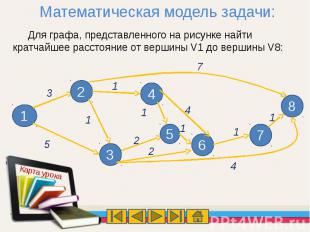
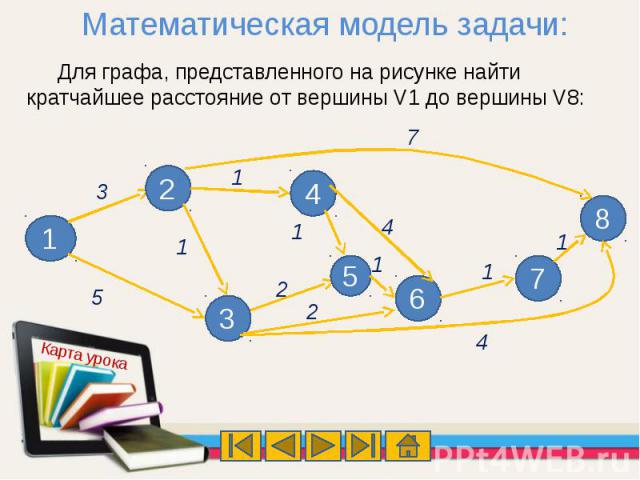
Математическая модель задачи:Для графа, представленного на рисунке найти кратчайшее расстояние от вершины V1 до вершины V8:

Требуется найти такой путь от начальной вершины V1 к конечной вершине V8 , чтобы сумма длин дуг, входящих в искомый путь, была минимальной. Определим искомые переменные следующим образом: 1, если ребро (Vi, Vj) входит в искомый кратчайший путьXij= 0, если ребро (Vi, Vj) не входит в кратчайший путьCij – длина дуги от вершины Vi до вершины Vj.Критериальная функцияС1,2X1,2+C1,3X1,3+….+C7,8X7,8 minОграничения:X1,2+X1,3+….+X1,8=1 – для вершины V1X1,8+X2,8+….+X7,8=1 – для вершины V8 ∑Xi,k - ∑Xk,j =0 - для остальных к-вершин

Компьютерная модель в формате Excel:

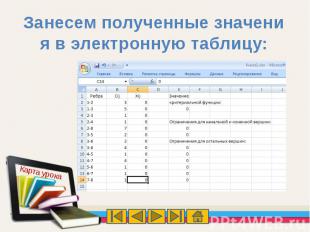
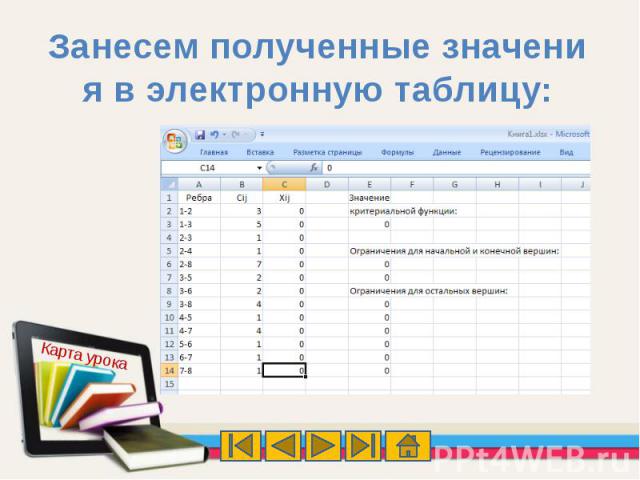
Занесем полученные значения в электронную таблицу:

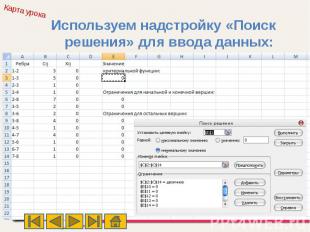
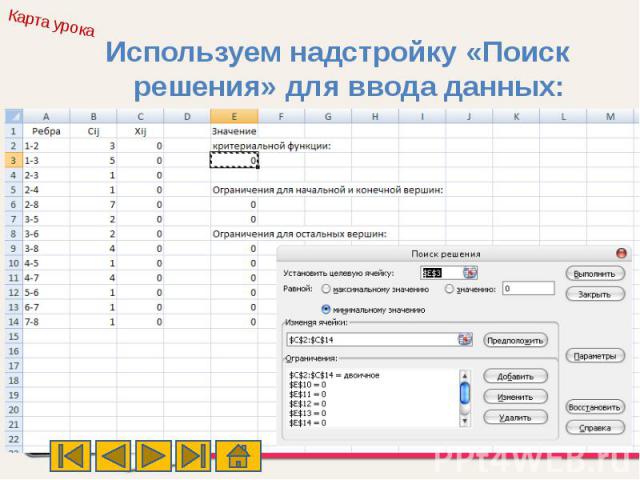
Используем надстройку «Поиск решения» для ввода данных:

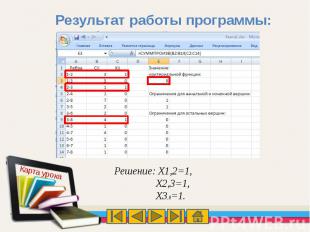
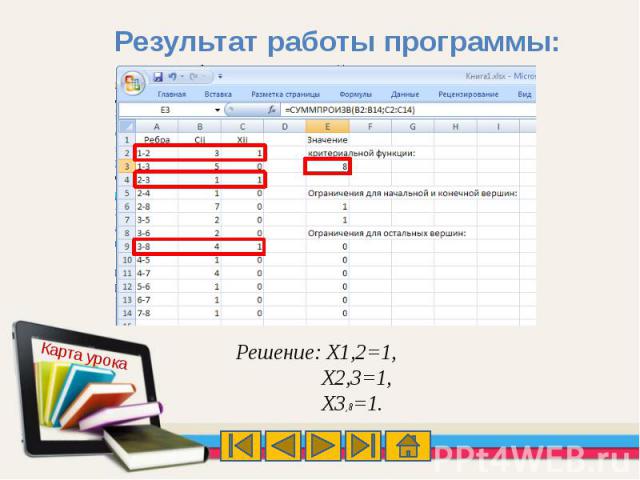
Результат работы программы:

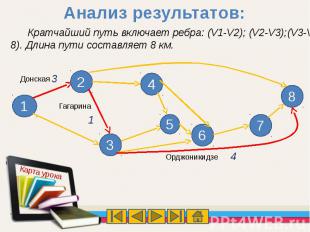
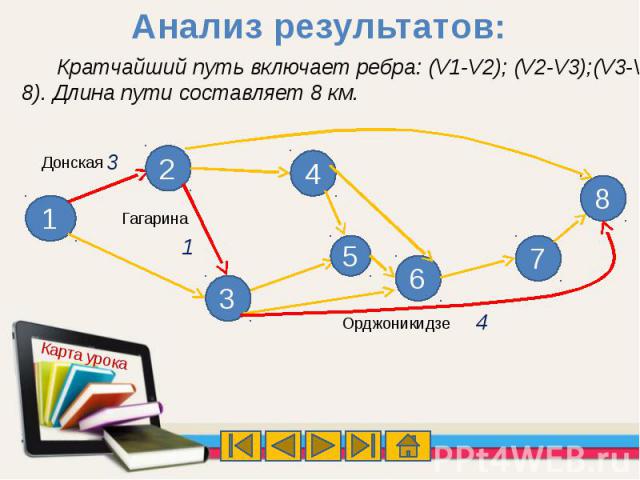
Кратчайший путь включает ребра: (V1-V2); (V2-V3);(V3-V8). Длина пути составляет 8 км.

Вернемся к вопросам, заданным в начале урока и постараемся ответить на них.

Изучить материалы конспекта. Построить математическую модель задачи:Решить задачу средствами MS Excel.Проанализировать результаты.Дана сеть автомобильных дорог Лазаревского района города Сочи. Ветеран войны решил проехать от дома ветеранов по ул. Калараша до площади кинотеатра «Восход». Каким маршрутом ему лучше ехать, чтобы путь был минимальным?

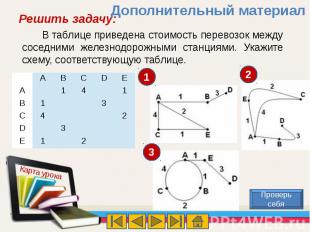
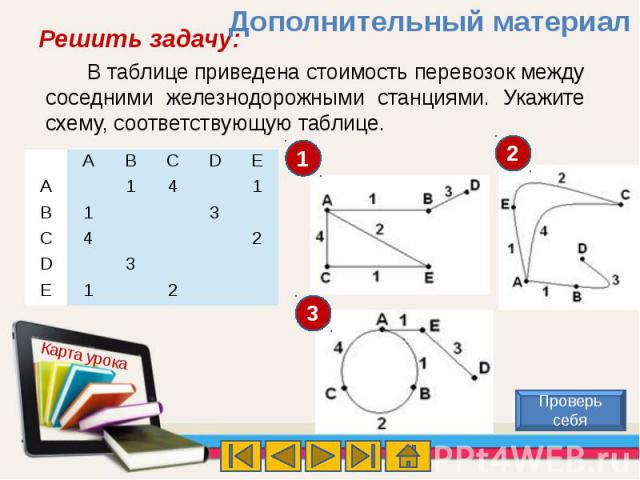
В таблице приведена стоимость перевозок между соседними железнодорожными станциями. Укажите схему, соответствующую таблице.

Спасибо за внимание!