Презентация на тему: Методы построения параллельных программ

Учебный курсВведение в параллельные алгоритмыЛекция 2Методы построения параллельных программ Якобовский М.В., д.ф.-м.н.Институт математического моделирования РАН, Москва

Предварительные замечания … если для нас представляют интерес реально работающие системы, то требуется убедиться, (и убедить всех сомневающихся) в корректности наших построений … системе часто придется работать в невоспроизводимых обстоятельствах, и мы едва ли можем ожидать сколько-нибудь серьезной помощи от тестовDijkstra E.W.1966

Содержание лекции Методы построения параллельных алгоритмов и их свойства:Статическая балансировкаметод сдваиваниягеометрический параллелизмконвейерный параллелизмДинамическая балансировкаколлективное решениеПример задачи, для параллельного решения которой необходимо создание качественно нового алгоритма

Хороший параллельный алгоритм Обладает запасом внутреннего параллелизмаЕсть возможность одновременного выполнения операцийДопускает возможность равномерного распределения вычислительных операций между процессорамиОбладает низким уровнем накладных расходов

Накладные расходы Операции, отсутствующие в наилучшем последовательном алгоритме:СинхронизацияОбмен даннымиДублирование операцийНовые операции
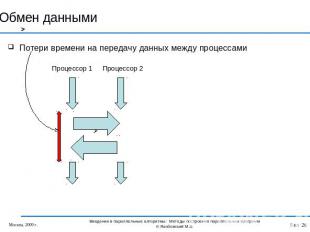
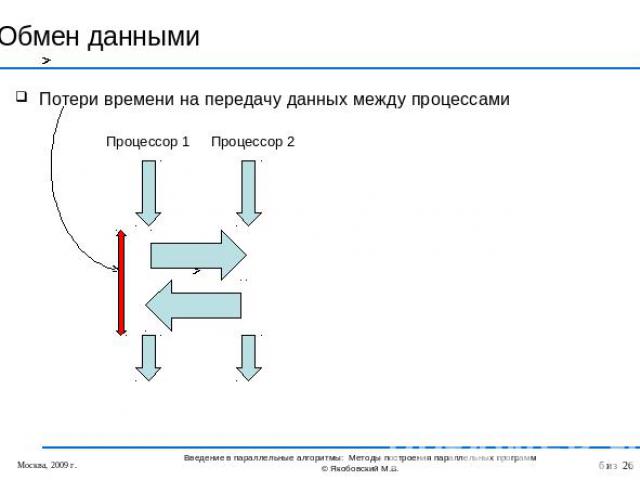
Обмен данными Потери времени на передачу данных между процессами Процессор 1 Процессор 2

Синхронизация Потери времени на ожидание долго выполняющихся процессов Процессор 1 Процессор 2 Процессор 3
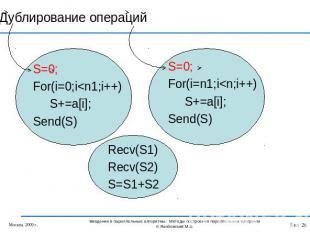
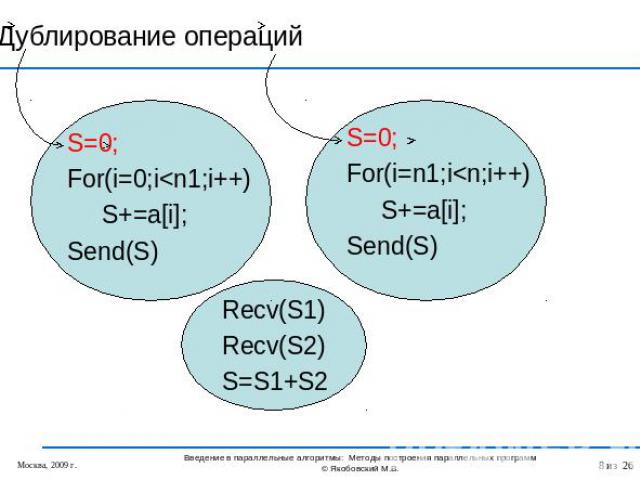
Дублирование операций

Вычисление всех факториалов до 8! включительно

Вычисление всех факториалов до 8! включительно

Метод сдванивания Каскадная схемаМодифицированная каскадная схема В.П.Гергель Основы параллельных вычислений, лекция 4, слайд 23
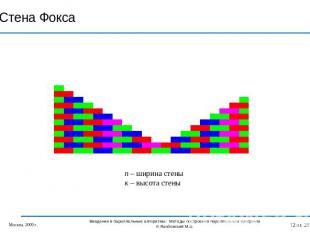
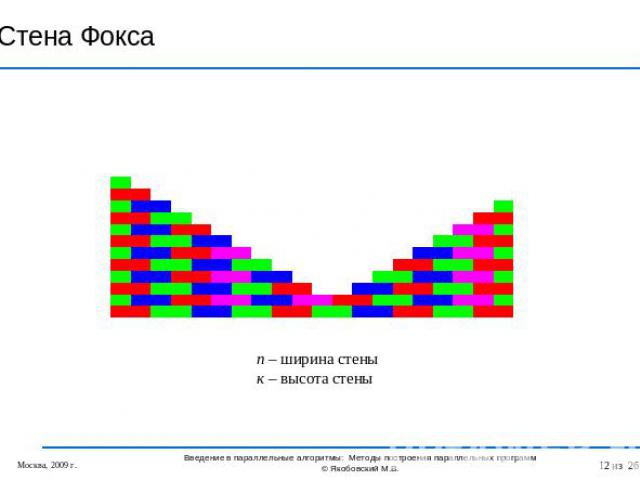
Стена Фокса
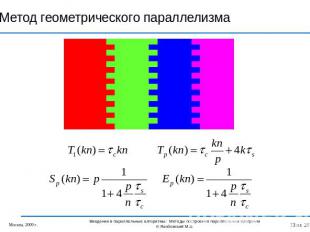
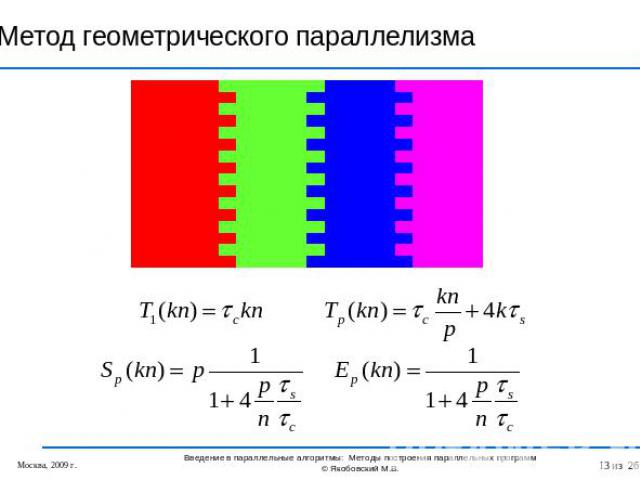
Метод геометрического параллелизма
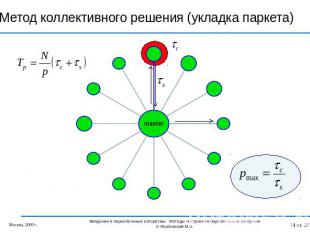
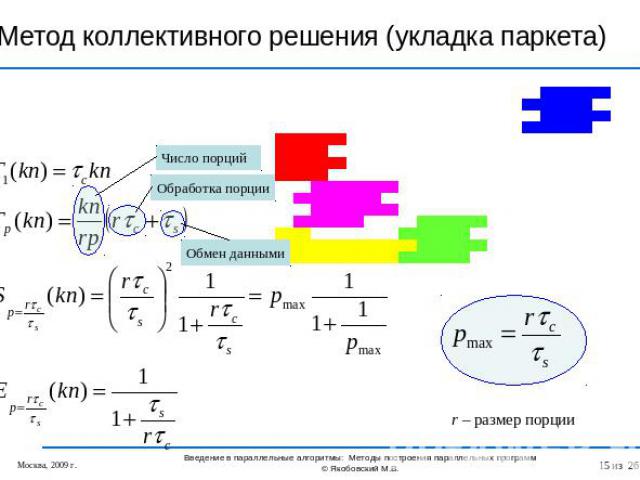
Метод коллективного решения (укладка паркета)
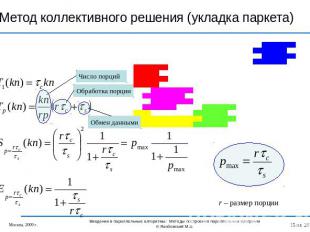
Метод коллективного решения (укладка паркета)
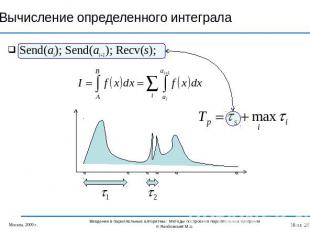
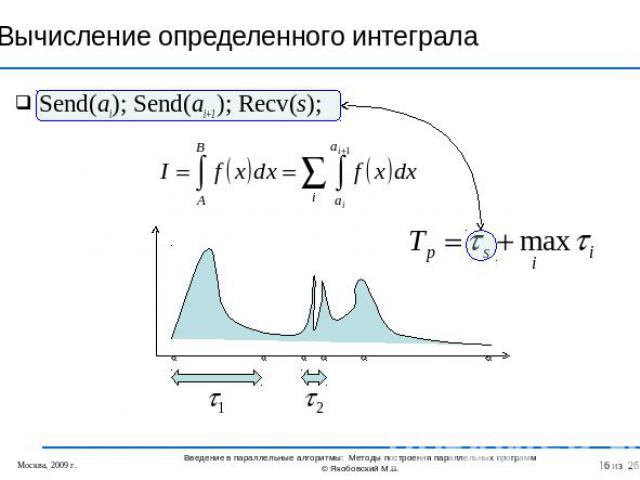
Вычисление определенного интеграла
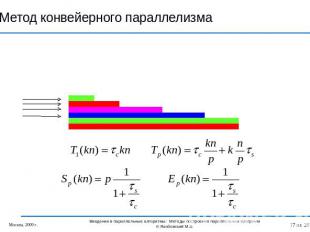
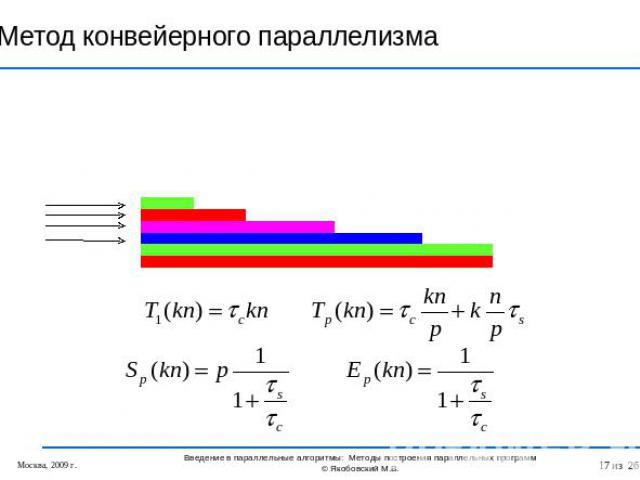
Метод конвейерного параллелизма

Статическая и динамическая балансировка загрузки процессоровСтатическая балансировкаметод сдваиваниягеометрический параллелизмконвейерный параллелизмДинамическая балансировкаколлективное решение

Определение суммы двух многоразрядных чисел
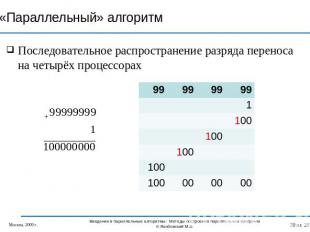
«Параллельный» алгоритм Последовательное распространение разряда переноса на четырёх процессорах

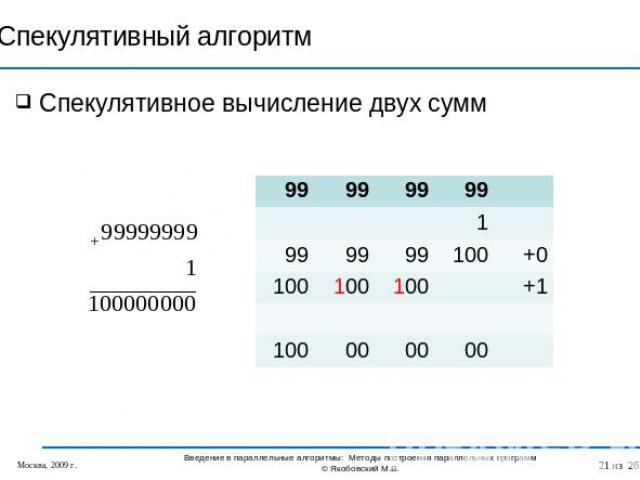
Спекулятивный алгоритм Спекулятивное вычисление двух сумм

Спекулятивный алгоритм
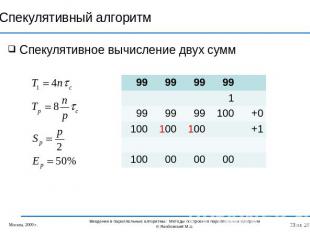
Спекулятивный алгоритм Спекулятивное вычисление двух сумм

Заключение Рассмотрены методы построения параллельных алгоритмовРассмотрена проблема балансировки загрузки процессоровПредставлен масштабируемый параллельный метод сложения многоразрядных чисел, основанный на неэффективном последовательном алгоритме

Вопросы для обсуждения В чем заключается проблема балансировки загрузки?В чем заключаются методы геометрического параллелизма, конвейерного параллелизма и коллективного решения?Чем определяются максимальные ускорения, достигаемые при применении этих методов?В чем отличие методов статической и динамической балансировки загрузки?

Контакты Якобовский М.В. д.ф.-м.н., зав. сектором «Программного обеспечения многопроцессорных систем и вычислительных сетей» Института математического моделирования Российской академии наукmail: [email protected] web: http://lira.imamod.ru