Презентация на тему: Двоичный код

Двоичный код

В связи с изобретением электронных вычислительных машин, которые обрабатывают информацию, представляемую электрическими импульсами, имеющими только два положения: ток есть – да – 1 тока нет – нет - 0возникла необходимость создания двоичного кода

Вспомним принцип, по которому записываются натуральные числа с помощью десятичного алфавита.

Попробуем применить ту же схему при записи чисел, учитывая, что мы имеем алфавит всего из двух цифр: 0 и 1.Таким образом, имея всего две цифры, можно представить любое число. Собственно говоря, совсем не важно, сколько цифр имеется в нашем алфавите. Применяя принцип позиции, мы можем записать любое число по аналогичному правилу.

Рассмотрим принципы перевода чисел из двоичной записи в десятичную и из десятичной в двоичную.

Другой способ перевода чисел из десятичной системы в двоичную - последовательное деление числа на 2 и запись остатков.

Другой способ перевода чисел из десятичной системы в двоичную - последовательное деление числа на 2 и запись остатков.
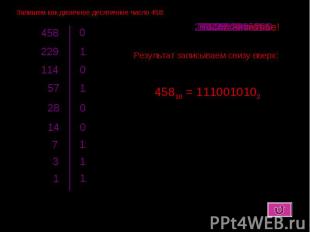
Запишем как двоичное десятичное число 458:
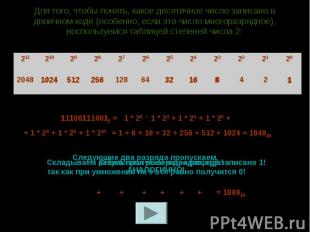
Для того, чтобы понять, какое десятичное число записано в двоичном коде (особенно, если это число многоразрядное), воспользуемся таблицей степеней числа 2:Складываем результаты всех разрядов, где записано 1!Следующие два разряда пропускаем, так как при умножении на 0 все равно получится 0!

Рассмотрим обратное задание – записать десятичное число в виде двоичногоВ этом случае можно снова воспользоваться таблицей степеней числа 2.Таким образом мы разложили исходное число на сумму слагаемых, которые представляют собой различные степени числа 2!

Так в привычном десятичном алфавите число 3824 можно представить как:поскольку здесь основание системы счисления – 2!

Правила записи натуральных чисел всем известны с начальной школы. Однако попробуем уловить суть этого процесса: Далее мы посмотрим, как это правило применимо к другим алфавитам