Презентация на тему: Алгебра суждений


Парадокс с карточкой математика П. Журдена

Основная задача логики высказываний заключается в том, чтобы на основании истинности или ложности простых высказываний определить истинность или ложность сложных высказываний. Среди сложных высказываний можно выделить: соединительные, разделительные, условные, эквивалентные, высказывания с внешним отрицанием.

Для булевых переменных определены следующие логические операции: Инверсия (логическое отрицание) , , not, не, (неверно, что…) 2) Конъюнкция (логическое умножение) , , &, and, и 3) Дизъюнкция (логическое сложение) +, V, or, или 4) Импликация (следование) , если…, то… 5) Двойная импликация или эквиваленция (равносильность) , =

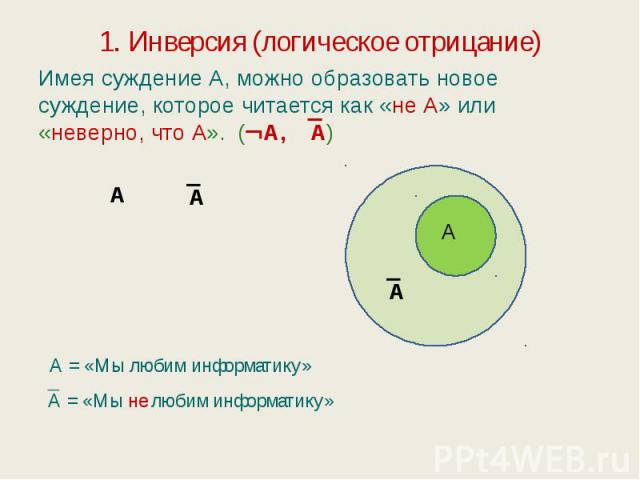
1. Инверсия (логическое отрицание) Имея суждение А, можно образовать новое суждение, которое читается как «не А» или «неверно, что А». ( А, А) А = «Мы любим информатику» А = «Мы не любим информатику»
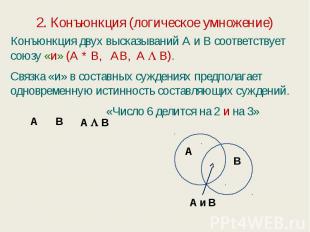
2. Конъюнкция (логическое умножение) Конъюнкция двух высказываний А и В соответствует союзу «и» (А * В, АВ, А В). Связка «и» в составных суждениях предполагает одновременную истинность составляющих суждений. «Число 6 делится на 2 и на 3»

3. Дизъюнкция (логическое сложение) Дизъюнкция двух суждений соответствует союзу «или» (А + В, А V В). Составное суждение со связкой «или» считается истинным, если истинно хотя бы одно из составных суждений, и считается ложным, если ложны все его составляющие. Объединяющее «или» «Петров является программистом или Петров является студентом»
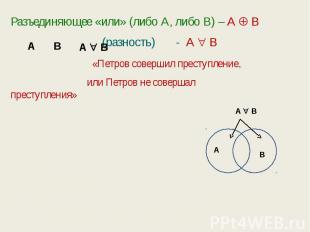
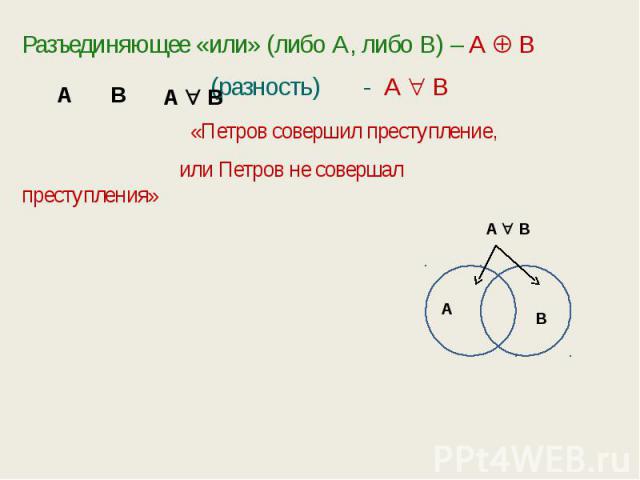
Разъединяющее «или» (либо А, либо В) – А В (разность) - А В «Петров совершил преступление, или Петров не совершал преступления»

4. Импликация (следование) А В ( Если А, то В. Из А следует В) Импликация ложна только в одном случае: «из истины не может следовать ложь, из лжи – все, что угодно». «Если 2 2 = 5, то 2 + 2 = 5» «Если 2 2 = 5, то 2 + 2 = 4»

Эквиваленция (равносильность, двойная импликация) Суждения А и В называются равносильными или эквивалентными, если они одновременно истинны или одновременно ложны. А = В ; А В ; А В ; А В А = «Этот треугольник равносторонний» В = «Этот треугольник равноугольный»

Приоритетность логических операций Инверсия Конъюнкция Дизъюнкция Импликация Эквиваленция

Всю совокупность формул логики высказываний можно разделить на 3 класса: нейтральные или выполнимые - выражения принимают значения как «истинно» так и «ложно»; тождественно-истинные формулы или тавтологии – выражения принимают значения «истинно» независимо от логических значений входящих в них переменных; тождественно-ложные формулы - выражения принимают значения «ложно» независимо от логических значений входящих в них переменных.