Презентация на тему: Основы стереометрии

О преподавании стереометрии в гуманитарных классах Автор: учитель математики высшей квалификационной категории Рзянина В. В. Балашов, 2006 МОУ «Гимназия имени Героя Советского Союза Ю. А. Гарнаева» 900igr.net

Первая четверть Что изучает стереометрия? Основные фигуры стереометрии. Пространственные фигуры. Параллельность прямых и плоскостей. Признаки параллельности плоскостей. Параллельное проектирование. Изображение пространственных фигур в параллельной проекции.

Вторая четверть Угол между прямыми в пространстве, перпендикулярность прямых. Угол между прямой и плоскостью. Перпендикулярность прямой и плоскости. Признак перпендикулярности прямой и плоскости. Расстояние между точкой и плоскостью. Перпендикуляр и наклонная. Угол между плоскостями, перпендикулярность двух плоскостей. Центральное проектирование. Изображение пространственных фигур в центральной проекции. Перспектива.

Третья четверть Многогранники. Параллелепипед, призма, пирамида. Правильные, полуправильные и звездчатые многогранники. Тела вращения: цилиндр, конус, шар. Взаимное расположение шара и плоскости. Касательная плоскость к шару. Понятие объема тел. Задачи измерения объема. Вычисление объемов параллелепипеда, призмы, пирамиды, цилиндра, конуса и шара. Площадь поверхности многогранников и тел вращения.

Четвертая четверть Прямоугольная система координат в пространстве. Координаты точки в пространстве. Расстояние между точками с заданными координатами. Векторы в пространстве. Координаты вектора. Сложение векторов и умножение вектора на число. Скалярное произведение векторов. Уравнение плоскости.

1-й урок: Что изучает стереометрия? Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве. Слово «стереометрия» происходит от греческих слов «стереос» - объемный, пространственный и «метрео» - измерять. Многие геометрические термины переведены с древнегреческого языка, т.к. геометрия зародилась в Древней Греции и развивалась в философских школах.

Одной из самых известных была пифагорейская школа, названная в честь основателя – Пифагора. Символом этой школы был звездчатый пятиугольник – пентаграмма.

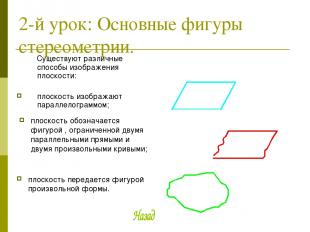
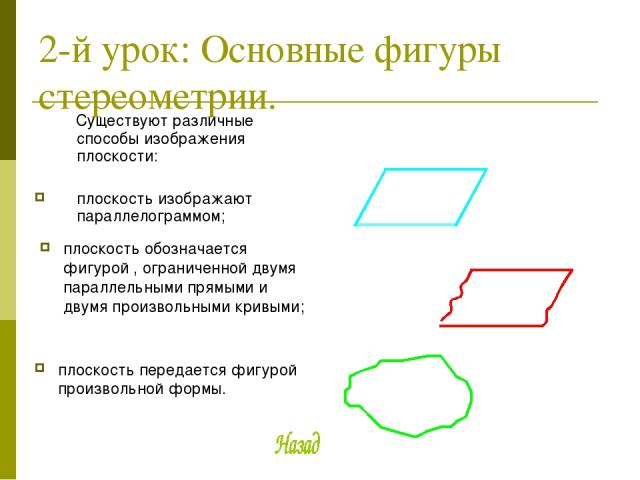
2-й урок: Основные фигуры стереометрии. Существуют различные способы изображения плоскости: плоскость изображают параллелограммом; плоскость обозначается фигурой , ограниченной двумя параллельными прямыми и двумя произвольными кривыми; плоскость передается фигурой произвольной формы.

3-й урок: Пространственные фигуры. Урок посвящается подготовке к введению аксиом стереометрии. Учащимся предлагаются следующие задачи: Изобразите прямую а, лежащую на ней точку А и не лежащую на ней точку В. Изобразите плоскость и две пересекающиеся прямые а и b , лежащие на ней. Изобразите плоскость , лежащие на ней точки А и В, а также точки C и D, расположенные на разные стороны от плоскости. Изобразите плоскость и пересекающую ее прямую а. Изобразите плоскости, пересекающиеся под прямым углом.

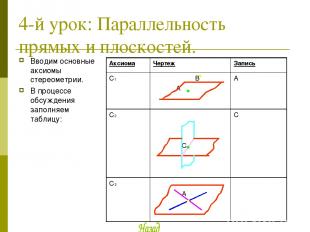
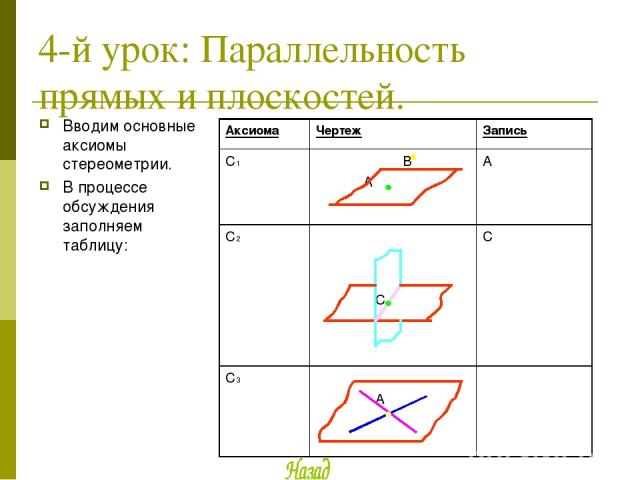
4-й урок: Параллельность прямых и плоскостей. Вводим основные аксиомы стереометрии. В процессе обсуждения заполняем таблицу: Аксиома Чертеж Запись С1 В А А С2 С С С3 А

5-й урок: Признаки параллельности плоскостей. При изучении аксиом стереометрии вспоминаем первые аксиомы планиметрии и формулируем их пространственные аналогии. В результате получаем следующую таблицу: Аксиома Чертеж Формулировка П1 Какова бы ни была прямая в пространстве, существуют точки пространства, принадлежащие этой прямой, и точки, не принадлежащие ей. П2 Через любые две точки пространства можно провести прямую, и притом только одну.

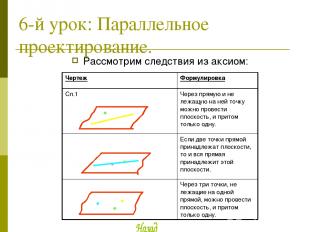
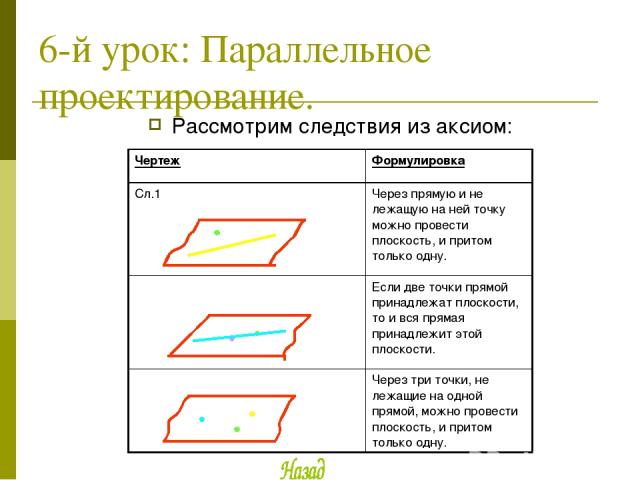
6-й урок: Параллельное проектирование. Рассмотрим следствия из аксиом: Чертеж Формулировка Сл.1 Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну. Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.

Изображение пространственных фигур на плоскости На тему отводятся семь занятий: Параллельное проектирование и его основные свойства; Параллельное проектирование плоских фигур; Изображение пространственных фигур в параллельной проекции; Сечение многогранников; Золотое сечение; Центральное проектирование и его свойства; Изображение пространственных фигур в центральной проекции.

Занятие 1: Параллельное проектирование и его основные свойства. Основные свойства параллельного проектирования: параллельной проекцией прямой является прямая или точка; параллельной проекцией отрезка является отрезок или точка; отношение длин отрезков, лежащих на одной прямой , сохраняется (в частности, середина отрезка при параллельном проектировании переходит в середину соответствующего отрезка); параллельной проекцией двух параллельных прямых являются параллельные прямые, или одна прямая, или две точки; отношение длин отрезков, лежащих на параллельных прямых, при параллельном проектировании сохраняется; если фигура лежит в плоскости, параллельной плоскости проектирования, то ее параллельной проекцией на эту плоскость будет фигура, равная исходной.

Занятие 2: Параллельные проекции плоских фигур. Рассматривается вопрос об изображении плоских фигур при параллельном проектировании. Учащиеся должны представить себе, какие фигуры являются параллельными проекциями многоугольников и окружности. Выяснить какие свойства многоугольников сохраняются при параллельном проектирования. Узнать как строятся параллельные проекци основных плоских фигур.

Занятие 3: Изображение пространственных фигур в параллельной проекции. На этом занятии учащиеся должны научиться правильно изображать основные пространственные фигуры, в том числе куб, прямоугольный параллелепипед, призму, цилиндр и конус.

Занятие 4: Сечение многогранников. Это занятие является решающим для выработки у учащихся представлений о взаимном расположении прямых и плоскостей в пространстве. Рассматриваются вопросы о построении сечений многогранников плоскостью.

Занятие 5: Золотое сечение. При изображении пространственных фигур важное место занимает вопрос о нахождении наилучшего соотношения неравных частей, составляющих вместе единое целое. Такое деление называют золотым сечением.

Учащиеся должны ознакомиться с этим понятием. Увидеть, как оно используется в: живописи; скульптуре; архитектуре.

Золотое сечение в скульптуре. Многие греческие скульпторов, такие как Фидий, Поликлет, Мирон, Пракситель использовали при создании своих творений принцип золотой пропорции.

Золотое сечение в архитектуре Известный русский архитекторы М. Казаков и В. Баженов широко использовали в своем творчестве “золотое сечение”. Например, “золотое сечение” можно обнаружить в архитектуре здания сената в Кремле. По проекту М. Казакова в Москве была построена Первой клинической Еще один архитектурный шедевр Москвы – дом Пашкова – является одним из наиболее совершенных произведений архитектуры В. Баженова.

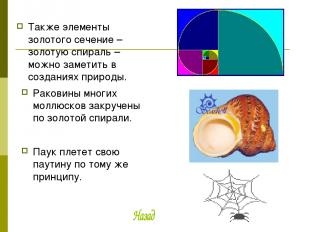
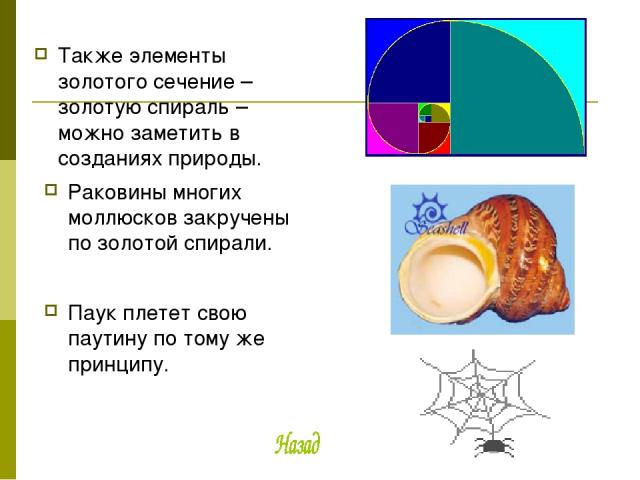
Также элементы золотого сечение – золотую спираль – можно заметить в созданиях природы. Раковины многих моллюсков закручены по золотой спирали. Паук плетет свою паутину по тому же принципу.

Занятие 6: Центральное проектирование и его свойства. Вначале рассматривается определение центрального проектирования. Рассматриваются различные случаи центрального проектирования.

Занятие 7: Изображение пространственных фигур в центральной проекции. В качестве примера рассматривается изображение куба. Также учащимся предлагаются задачи.

Многогранники. В этот курс включены следующие занятия: Правильные многогранники. Полуправильные многогранники. Звездчатые многогранники. Теорема Эйлера.

Занятие 1: Правильные многогранники. В начале урока вводится определение выпуклого многогранника: «Выпуклым называется многогранник, если он расположен по одну сторону от плоскости каждой его грани». Рассматриваются модели выпуклых многогранников.

составлена из n-угольников и n треугольников

составлена из двух равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов

составлен из двадцати равносторонних треугольников

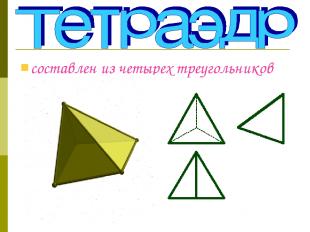
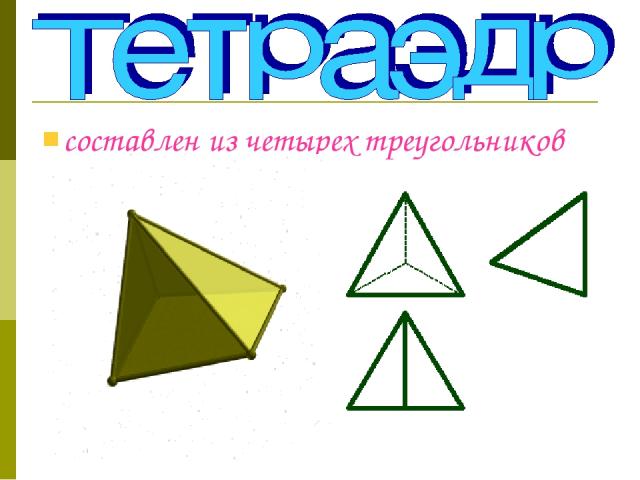
составлен из четырех треугольников

составлен из восьми равносторонних треугольников

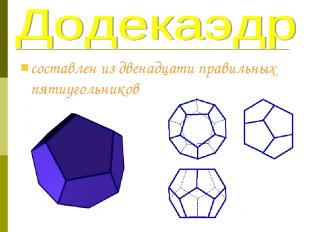
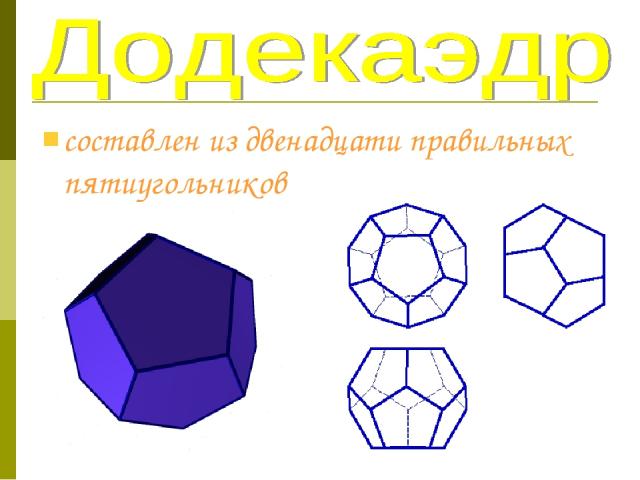
составлен из двенадцати правильных пятиугольников

составлен из шести квадратов, также называется КУБ

Занятие 2: Полуправильные многогранники. Вводится определение полуправильного многогранника. Демонстрируются модели.

Занятие 3: Звездчатые многогранники. Рассматриваются правильные звездчатые многогранники.

Занятие 4: Теорема Эйлера. Одно из наиболее интересных свойств выпуклых многогранников описано теоремой Эйлера. Сначала с учащимися рассматриваются известные им многогранники и заполняется таблица. Затем выводится и сама теорема: В-Р+Г=2 Название многогранника Число вершин(В) Число ребер (Р) Число граней (Г) Треугольная пирамида 4 6 4 Четырехугольная призма 8 12 6 Пятиугольная бипирамида 7 15 10 правильный додекаэдр 20 30 12 n-угольная пирамида n+1 2n n+1 n-угольная призма 2n 3n n+2

Углы между прямыми и плоскостями в пространстве. При изучении данной темы желательно отметить, что проблема измерения углов восходит к глубокой древности. Следует как можно шире осветить историю создания измерительных приборов и методы измерения. Для это предлагается провести следующие занятия: Объем фигур в пространстве. Объем цилиндра; Принцип Кавальери; Объем конуса; Объем шара.

Занятие 1: Объем фигур в пространстве. Объем цилиндра. На этом занятии рассматриваются проблемы измерения объемов пространственных фигур. Перечисляются основные свойства объема: объем фигуры в пространстве является неотрицательным числом; объем куба с ребром 1 равен 1; равные фигуры имеют равные объемы; если фигура Ф составлена из фигур Ф1 и Ф2, то объем фигуры Ф равен сумме объемов фигур Ф1 и Ф2.

Занятие 2: Принцип Кавальери. Дается формулировка принципа Кавальери. Применяя данный принцип решаем задачи.

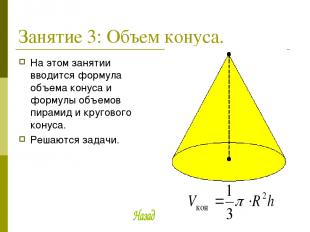
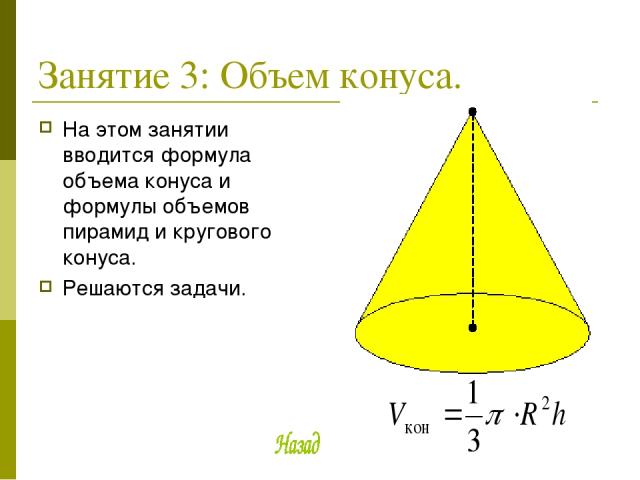
Занятие 3: Объем конуса. На этом занятии вводится формула объема конуса и формулы объемов пирамид и кругового конуса. Решаются задачи.

Занятие 4: Объем шара. На занятии выводится формула объема шара: Решаются задачи по данной теме.

Координаты и векторы в пространстве. Нами были разработаны и проведены следующие занятия: Определение и простейшие примеры фигур вращения. Фигуры вращения. Вращение многогранников. Комбинации различных движений.

Занятие 1: Определение и простейшие примеры фигур вращения. Дается определение фигуры вращения, а также понятие поворота в пространстве относительно прямой. Рассматриваются задачи по данной теме. Учащимся предлагаются задачи для самостоятельной работы.

Занятие 2: Фигуры вращения. Рассматриваются фигуры, которые можно получить вращением кривых и криволинейных трапеций. Рассматриваются кривые, криволинейные трапеции, их свойства. Для самостоятельной работы учащимся предлагаются различные задачи.

Занятие 3: Вращение многогранников. Рассматриваются фигуры в пространстве, получающиеся вращение различных многогранников. Решаются задачи. Даются задания для самостоятельной работы.

Занятие 4: Комбинации различных движений. Рассматриваются фигуры в пространстве, получающиеся комбинацией различных движений.