Презентация на тему: Закон сохранения энергии

Закон сохранения энергии Цель: дать понятие полной механической энергии, закона сохранения энергии, практическое применение закона сохранения энергии 900igr.net

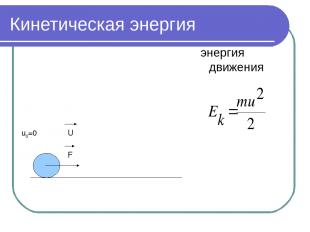
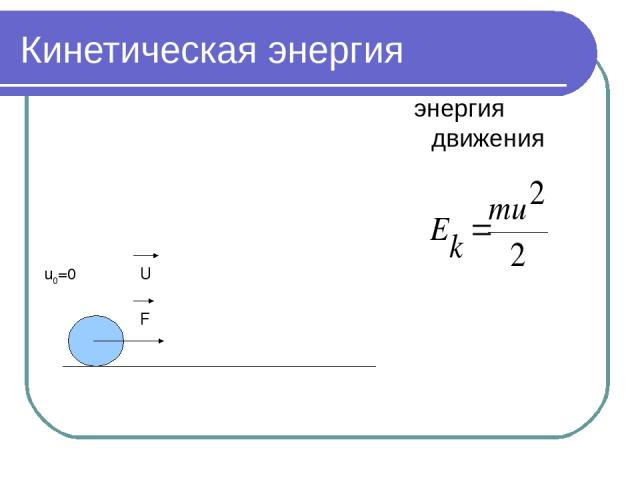
Кинетическая энергия энергия движения u0=0 F U

Герман Гельмгольц Впервые математически обосновал закон сохранения энергии, показав его всеобщий характер.Разработал термодинамическую теорию химических процессов, ввел понятия свободной и связанной энергий. Заложил основы теорий вихревого движения жидкости и аномальной дисперсии. Является автором основополагающих трудов по физиологии слуха и зрения. Обнаружил и измерил тепло-образование в мышцах, изучил процесс сокращения мышц, измерил скорость распространения нервного импульса. Автор фундаментальных трудов по физике, биофизике, физиологии, психологии.

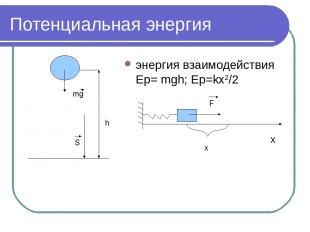
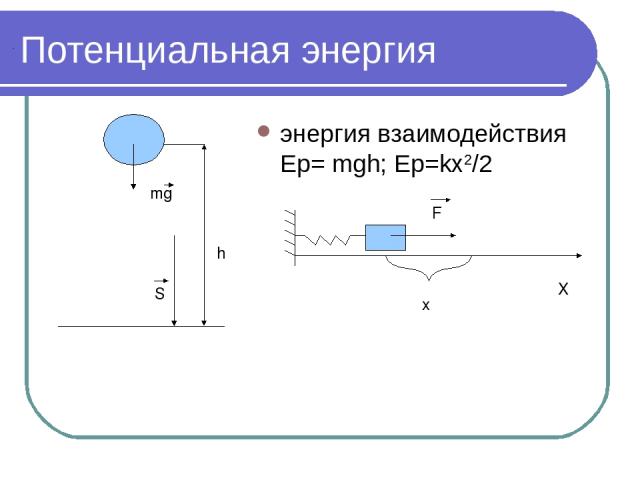
Потенциальная энергия энергия взаимодействия Ep= mgh; Ep=kx2/2 h mg S x F X

Полная механическая энергия Е=Ек+Еp

Закон сохранения энергии 1847г «Если тела действуют друг на друга с силами, не зависимыми от времени и скорости, сумма живых и напряженных сил останется постоянной»

∆Е= ∆ Ек + ∆ Еp, но А= ∆Ек, а ∆Еp=∆t Еp-А пот ∆Е=А+∆t Еp-А пот Работа всех сил, действующих Работа потенциальных сил на частицы системы (и потенциальных, и сил трения) А-Апот=Атр ∆Е=∆t Еp+ Атр

Теорема об изменении механической энергии Изменение механической энергии системы равно сумме работы сил трения и изменения во времени потенциальной энергии, обус-ловленного нестационарностью (т.е. зависимостью от времени) действующих на систему сил.

Эмми Нётер Труды Нетер по алгебре способствовали созданию нового направления, названного общей алгеброй. Сформулировала фундаментальную теорему теоретической физики, которая устанавливает связь между свойствами симметрии физической системы и законами сохранения. Если свойства системы не меняются при каком-либо преобразовании переменных, то этому соответствует сохранение некоторой физической величины. Так, независимости свойств системы от выбора начала отсчета времени соответствует закон сохранения энергии.

Теорема Нётер Каждому свойству симметрии пространства и времени соответствует свой закон сохранения энергии

Закон сохранения энергии При любых процессах, происходящих в замкнутой, потенциальной системе, её полная механическая энергия остается постоянной Е=const

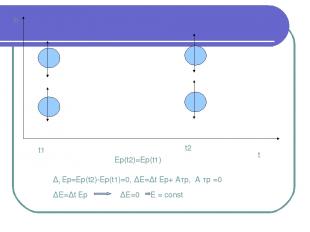
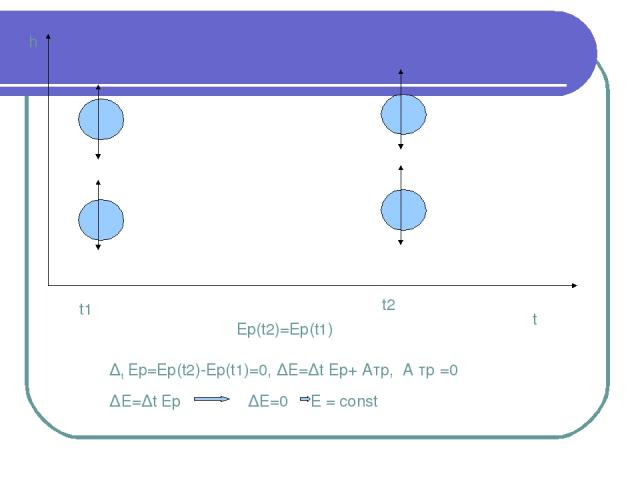
h t t1 t2 Ep(t2)=Ep(t1) ∆t Еp=Ep(t2)-Ep(t1)=0, ∆Е=∆t Еp+ Атр, А тр =0 ∆Е=∆t Еp ∆Е=0 E = const

Закон сохранения энергии При любых процессах, происходящих в консервативных системах, её полная механическая энергия остается постоянной E=const

Ek + Ep =const В процессе движения системы всякое увеличение кинетической энергии системы должно сопровождаться соответствующим уменьшением её потенциальной энергии и наоборот

– давление горизонтально текущей жидкости (или газа) больше в тех местах потока, в которых скорость ее течения меньше, и, наоборот, в тех местах потока, где скорость больше, давление меньше. Закон Бернулли U1,p1 U2, p2 P1>P2, U1

Даниил Бернулли (1700-1782) Закон Бернулли справедлив для идеальной жидкости (т. е. жидкости, в которой можно пренебречь силами внутреннего трения) и является следствием закона сохранения энергии

Этим явлением объяс-няется и возникновение подъемной силы, дейст-вующей на крылья самолета.

Николай Егорович Жуковский(1847-1921) Теория возник-новения подъемной силы крыла само-лета была разра-ботана русским ученым Николаем Егоровичем Жуковским.

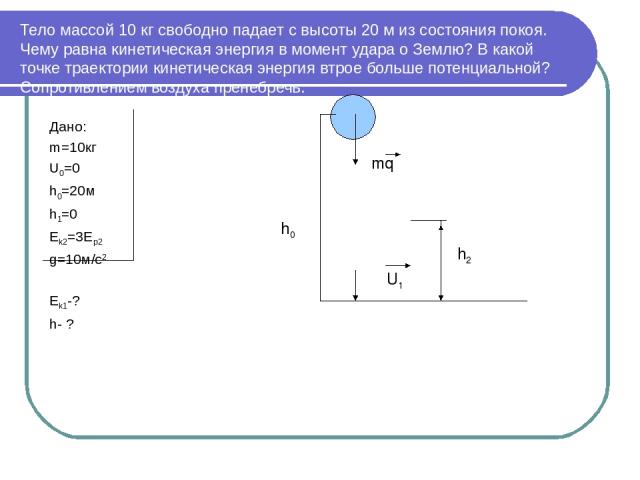
Тело массой 10 кг свободно падает с высоты 20 м из состояния покоя. Чему равна кинетическая энергия в момент удара о Землю? В какой точке траектории кинетическая энергия втрое больше потенциальной? Сопротивлением воздуха пренебречь. Дано: m=10кг U0=0 h0=20м h1=0 Ek2=3Ep2 g=10м/с2 Ek1-? h- ? mq U1 h0 h2

Еp0+Ek0=Ep1+Ek1 U0=0 и h1=0 Ek1=mgh0, Ek1= 10*10*20=2000 Дж Запишем закон сохранения энергии для точки траектории, где E k2= 3Eр2 , Еp0+E k0= E k2+ Eр2, Eр0= 4 Eр2, m g h0= 4 m g h2 Ответ: E k1=2000 Дж, h2= 5 м.

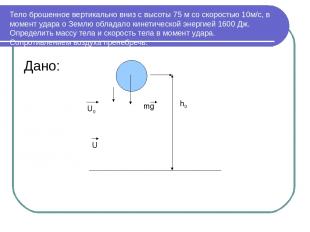
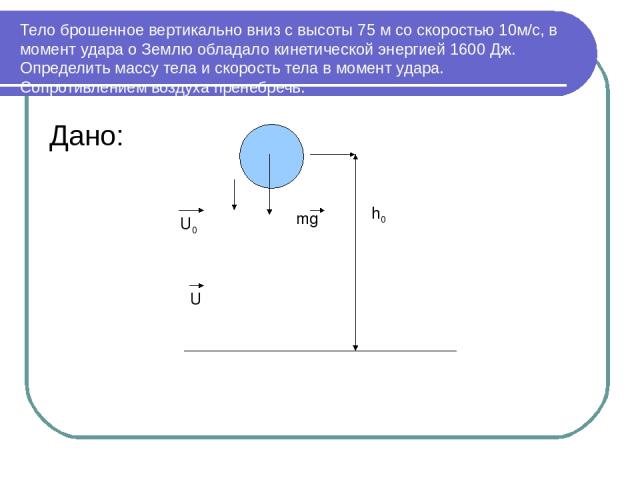
Тело брошенное вертикально вниз с высоты 75 м со скоростью 10м/с, в момент удара о Землю обладало кинетической энергией 1600 Дж. Определить массу тела и скорость тела в момент удара. Сопротивлением воздуха пренебречь. Дано: U0 h0 mg U