Презентация на тему: Понятие кинематики

Курс общей физики проф. Тюрин Юрий Иванович Томский политехнический университет ФТИ Адрес: пр. Ленина, 43, г.Томск, Россия, 634034 [email protected], Тел. 8-3822-563-621 Факс 8-3822-563-403 900igr.net

Лекция 2 Тема: МЕХАНИКА Введение 2. КИНЕМАТИКА 2.1. Введение 2.2. Векторные величины 2.3. Кинематика поступательного движения материальной точки 2.4. Мгновенная скорость 2.5. Ускорение 2.6. Кинематика вращательного движения Содержание лекции: Сегодня: *

1. Введение Механическое движение – это изменение с течением времени взаимного расположения тел или их частей. Механика – часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение.

Развитие механики как науки начинается с III в. до н.э., когда древнегреческий ученый Архимед (287 – 212 г.г. до н.э.) сформулировал закон равновесия рычага и законы равновесия плавающих тел. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем и окончательно сформулированы английским ученым И. Ньютоном. Механика Галилея – Ньютона называется классической механикой, т.е. она рассматривает движение микроскопических тел со скоростями, значительно меньшими скорости света в вакууме.

2. Кинематика движения материальной точки. 2.1. Введение Кинематика (от греческого слова kinēma движение) раздел механики, в котором изучаются геометрические свойства движения тел без учета их массы и действующих на них сил. Исходными понятиями в кинематике являются такие фундаментальные физические понятия, как пространство и время. Пространство выражает порядок сосуществования отдельных физических объектов. Время порядок смены явлений.

Свойства пространства и времени задаются не философскими теориями, а являются предметом естественно-научного исследования. Такие общие свойства пространства и времени были установлены. При движении тела со скоростями много меньшими скорости света (с = 299792458 м с 1) пространство является евклидовым и время течет одинаково во всех системах отсчета область классического поведения физических объектов. Пространство однородно и изотропно в пространстве нет выделенных положений и направлений. Все точки пространства равноправны и все направления эквивалентны.

Однородность времени означает, что все моменты времени эквивалентны и нет какого-либо выделенного начала отсчета для протекания любого физического явления. Время однонаправлено и протекает из прошлого в будущее. При скоростях движения, близких к скорости света, пространство и время образуют единый четырехмерный пространственно-временной континуум. При больших скоростях движения, близких к 3 108 м/c, размеры предметов и временной интервал между событиями не являются инвариантами и зависят от выбора системы отсчета.

2.2. Векторные величины Рассматривая движение на плоскости, приходится складывать и вычитать перемещения, которые не всегда бывают направленными в одну и ту же сторону. Для упрощения этих действий пользуются математическим понятием вектора. Вектор представляет собой математическую величину, характеризуемую длиной и направлением. Пусть за время t шарик пролетел расстояние х по горизонтали и y по вертикали. Тогда полное линейное перемещение шарика за время t запишется в виде

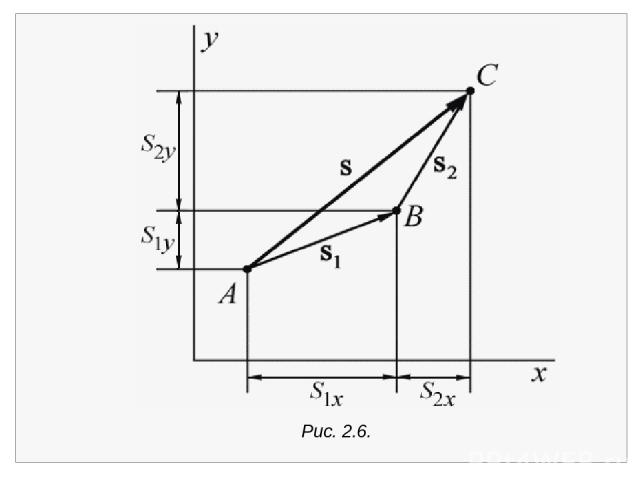
Рис. 2.1. Соотношение между полным перемещением r и его составляющими х, у по осям х и у На рис. 2.2 показано, как складываются два вектора. Вектор s1 представляет собой перемещение из точки А в точку В, а s2 – перемещение из точки В в точку С. Результирующее перемещение из А в С s представляет собой векторную сумму s1 + s2. Из рис. 2.2 мы видим, что sx = s1x + s2x, sy = s1y + s2y. Величина r определяет величину вектора перемещения r.

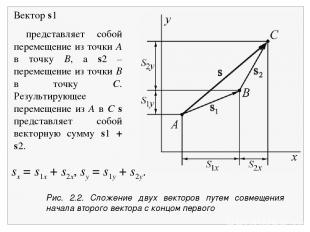
Рис. 2.2. Сложение двух векторов путем совмещения начала второго вектора с концом первого Вектор s1 представляет собой перемещение из точки А в точку В, а s2 – перемещение из точки В в точку С. Результирующее перемещение из А в С s представляет собой векторную сумму s1 + s2. sx = s1x + s2x, sy = s1y + s2y.

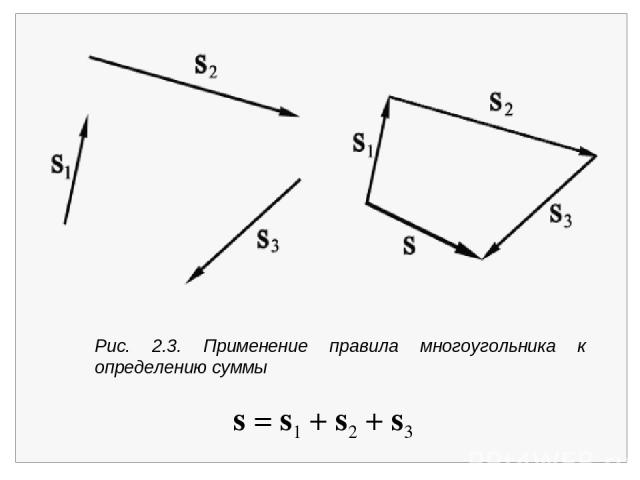
В учебниках векторы обозначаться жирными буквами, например s, а длины векторов – светлыми курсивными буквами, например s, либо в виде s . В конспектах вектора удобнее обозначать стрелкой над буквой а. Длина вектора всегда положительна. Векторное уравнение s = s1 + s2 представляет собой сокращенную форму записи приведенных выше двух уравнений sx = s1x + s2x, sy = s1y + s2y. Отметим, что если векторы s1 и s2 не являются параллельными, то для суммы s = s1 + s2 справедливо неравенство s < s1 + s2. Более того, иногда величина s может оказаться меньше любого из ее слагаемых. Такой случай показан на рис. 2.3.

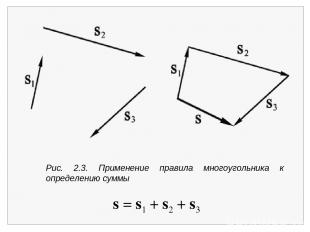
Рис. 2.3. Применение правила многоугольника к определению суммы s = s1 + s2 + s3

В физике часто приходится иметь дело с векторными величинами. К ним относятся перемещение тела, скорость, ускорение, сила, импульс, момент импульса, момент силы, электрическое поле, магнитное поле и плотность тока. Если вектор умножить (или разделить) на число, то результирующая величина также будет вектором. Например, при делении перемещения r на t получаем вектор скорости: v (определение скорости). При делении вектора v на t получаем вектор ускорения: (определение ускорения) (символ “ ” означает здесь “по определению”).

Рис. 2.4. Три единичных вектора i, j и k Произвольный вектор r можно задать тремя его составляющими x, y, z. Общепринята следующая запись: r = ix + jy + kz, где i, j, k – единичные векторы, направленные вдоль осей x, y, z соответственно. Например, как показано на рис. 2.4, вектор i имеет единичную длину и направлен вдоль оси х.

2.3. Кинематика поступательного движения материальной точки В классической кинематике рассматривается движение материальной точки в евклидовом пространстве с абсолютным временем, единым для всех систем отсчета. Материальная точка физический объект, размерами которого можно пренебречь по сравнению с пройденным расстоянием. Например, радиус Земли R = 6,4 106 м, радиус орбиты Земли r = 1,5 1011 м. То есть Землю можно рассматривать в качестве точки на околосолнечной орбите. Кинематика точки является основой изучения движения тел произвольных линейных размеров.

Выберем прямоугольную систему координат. Положение точки относительно данной системы отсчета задается радиус-вектором r = r(t), т.е. набором трех проекций координат точки на оси x, y, z, как функций времени: r = ix(t) + jy(t) + kz(t), В международной системе СИ, r измеряется в метрах (м). Линия, описывающая изменение положения конца радиус-вектора r со временем, называется траекторией движения (рис. 2.5).

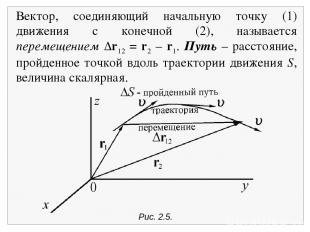
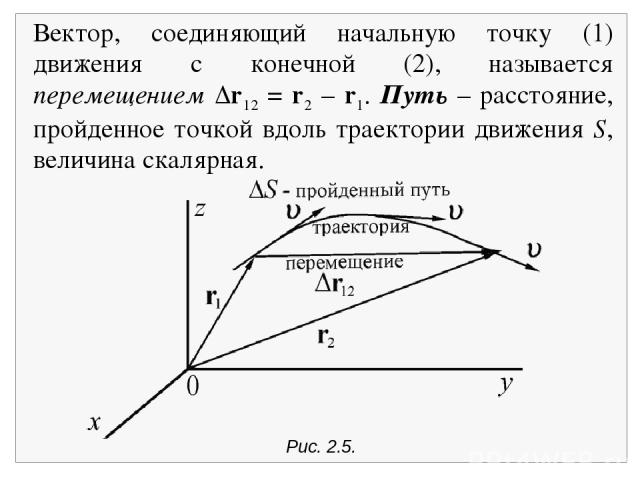
Рис. 2.5. Вектор, соединяющий начальную точку (1) движения с конечной (2), называется перемещением r12 = r2 – r1. Путь – расстояние, пройденное точкой вдоль траектории движения S, величина скалярная.

2.4. Мгновенная скорость Скорость – это быстрота изменения положения тела в пространстве. Мгновенной скоростью называют величину, равную производной от радиус-вектора тела по времени v = Производная равна скорости изменения функции при изменении аргумента. Через vx, vy, vz обозначены проекции вектора скорости на оси x, y, z

Вектор скорости v направлен по касательной к траектории движения. Величина вектора скорости в каждой точке траекторий равна Время в СИ измеряется в секундах, длина в метрах, скорость в [метрах за секунду] = [м/с]. Средняя величина скорости точки равна отношению пути S ко времени t, за который этот путь пройден: vср = . Здесь S – пройденный путь за время t.

Средний вектор скорости определяется как отношение вектора перемещения r ко времени t, за которое это перемещение произошло vср = , где r = i(x2 – x1) + j(y2 – y1) + k(z2 – z1), t = t2 – t1. В случае движения с малыми скоростями, много меньшими скорости света, скорость тела, участвующего одновременно в нескольких движениях, может быть найдена по правилу сложения векторов v = v 1 + v2, где v1 – скорость тела относительно системы отсчета K1, v2 – скорость движения системы K1 относительно "неподвижной" системы K2.

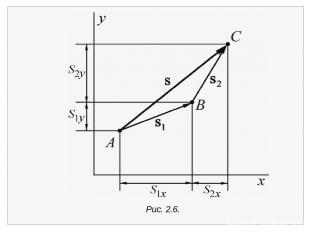
Рис. 2.6.

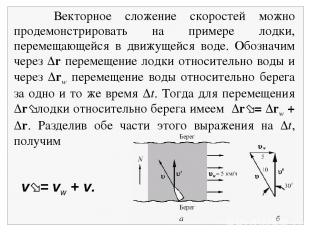
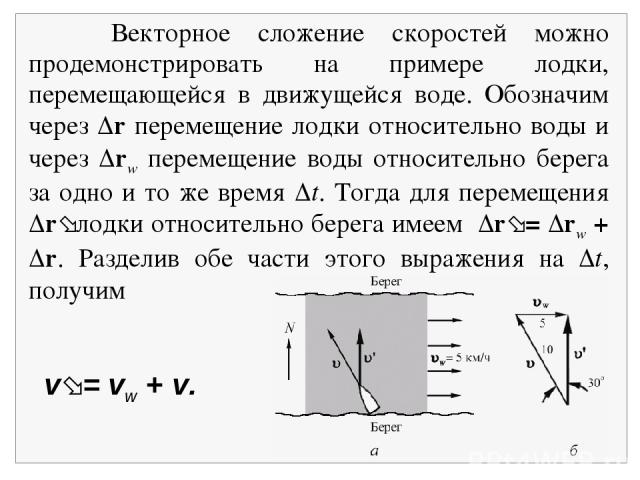
v = vw + v. Векторное сложение скоростей можно продемонстрировать на примере лодки, перемещающейся в движущейся воде. Обозначим через r перемещение лодки относительно воды и через rw перемещение воды относительно берега за одно и то же время t. Тогда для перемещения r лодки относительно берега имеем r = rw + r. Разделив обе части этого выражения на t, получим

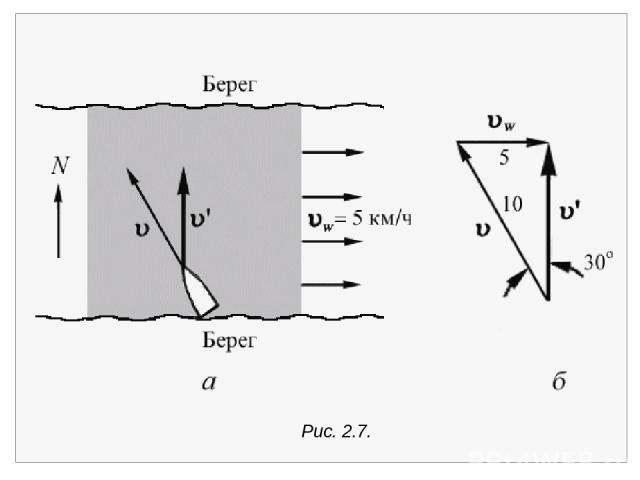
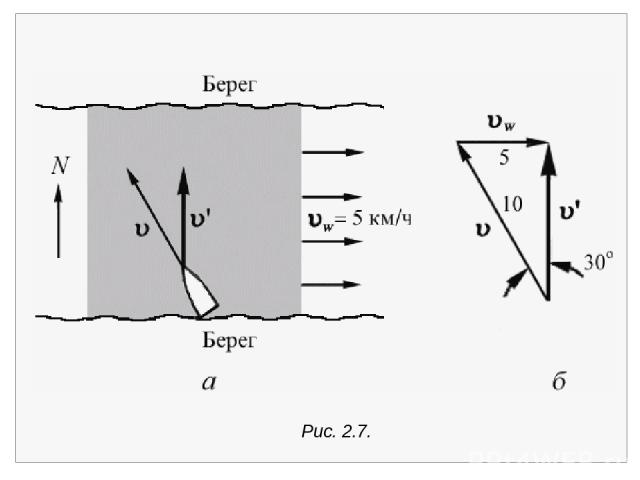
В приводимом примере через v обозначена скорость лодки в системе отсчета (в системе координат), которая покоится относительно воды. Эту скорость измеряют те, кто находится на борту лодки, если они не видят берегов. Наблюдатель в другой системе отсчета, а именно связан ной с берегом, видит иную скорость дви жения лодки v , которая дается написанным выше соотношением. Пусть, например, лодка пытается пересечь реку, теку щую, как показано на рис. 2.7 , на восток со скоростью 5 км/ч. Рулевому известна скорость лодки относительно воды: 10 км/ч. Как надо править, чтобы паром двигался поперек реки, и какой будет скорость парома относительно берега?

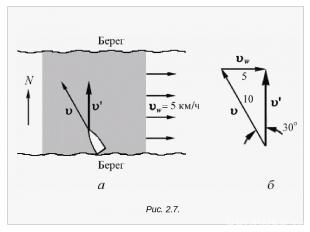
Рис. 2.7.

Обозначим через v вектор скорости парома относительно воды, а через vw – скорость воды. На рис. 2.7, б показан треугольник, составленный из этих векторов. Один угол в этом треугольнике прямой, а два других равны 30° и 60°, поскольку гипотенуза треугольника в два раза длиннее одного из ка тетов. Следовательно, рулевой должен держать курс под углом 30° к северо-западу. Величина вектора v равна 10 км/ч cos 30°, т.е. 8,66 км/ч. Заметим, что она меньше суммы ве личин слагаемых: 8,66 < 10 + 5 км/ч.

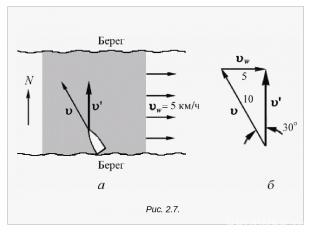
Рис. 2.7.

2.5. Ускорение Ускорением называется физическая величина, равная скорости изменения скорости первая производная от v по t или вторая производная от r по t: Поскольку скорость – векторная величина, а вектор задается своим модулем – длиной |v| = и направлением, то и изменяться вектор v со временем может двумя способами: по величине и по направлению.

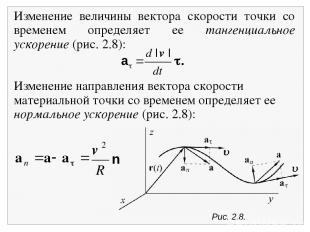
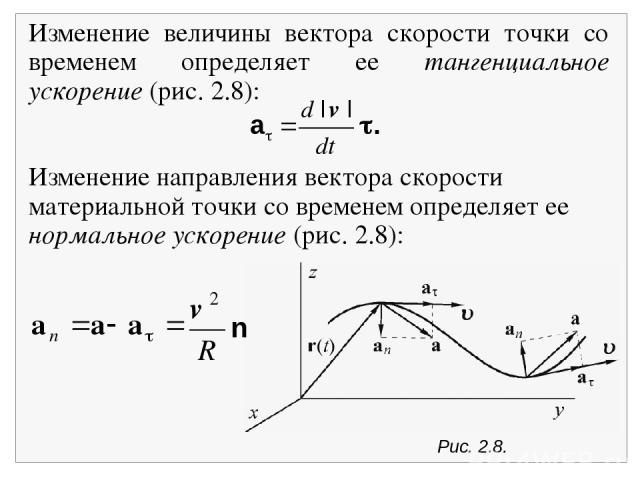
Рис. 2.8. n Изменение величины вектора скорости точки со временем определяет ее тангенциальное ускорение (рис. 2.8): a . Изменение направления вектора скорости материальной точки со временем определяет ее нормальное ускорение (рис. 2.8):

Здесь: – единичный вектор, направленный параллельно вектору скорости v, т.е. по касательной к траектории движения = ; n – вектор нормали, перпендикулярный вектору , т.е. (n, ) = 0, где круглые скобки означают скалярное произведение векторов; R – радиус кривизны траектории движения в точке, где определяется скорость движения – радиус окружности касательной в данной точке к искривленной траектории движения. Чем меньше радиус окружности, тем сильнее кривизна траектории в данной точке, тем быстрее изменяется вектор скорости по направлению, тем больше нормальное ускорение. По определению, имеем:

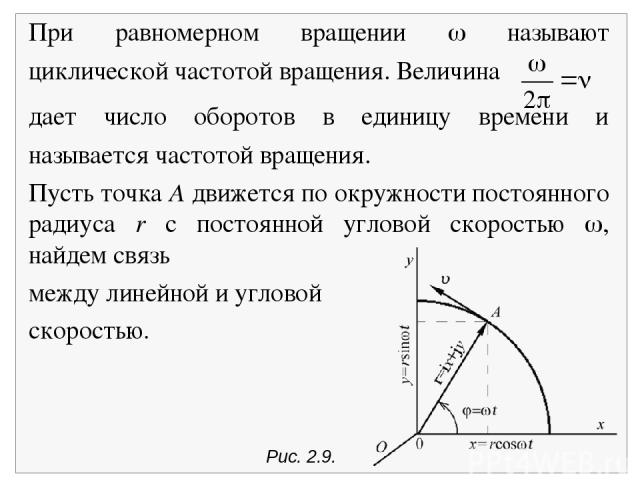
2.6. Кинематика вращательного движения По аналогии с линейной скоростью и ускорением вводятся угловая скорость и угловое ускорение. Эти понятия относятся к случаю движения материальной точки по окружности. Положение точки А на окружности можно задать углом , который образует радиус-вектор r с неизменным направлением оси х (рис. 2.9). Величина угловой скорости точки равна углу поворота радиус-вектора точки в единицу времени Вращение называется равномерным, если угловая скорость постоянна, в этом случае угол поворота линейно растет со временем: = 0 + t.

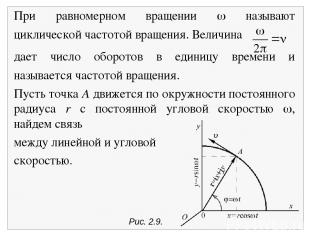
Рис. 2.9. При равномерном вращении называют циклической частотой вращения. Величина дает число оборотов в единицу времени и называется частотой вращения. Пусть точка А движется по окружности постоянного радиуса r с постоянной угловой скоростью , найдем связь между линейной и угловой скоростью.

Движение точки по круговой траектории описывается уравнением r(t) = ix(t) + jy(t) = r(i cos t + j sin t), где i, j единичные векторы, направленные вдоль осей x и y соответственно. Вектор скорости материальной точки, движущейся по окружности неизменного радиуса с постоянной скоростью, равен v Вектор v направлен по касательной к окружности, т.е. перпендикулярно r, поскольку их скалярное произведение равно нулю (v,r) = 0. Величина вектора скорости равна

Найдем ускорение точки, равномерно вращающейся по окружности, и связанное только с изменением направления вектора скорости, т.е. нормальное ускорение an = = 2r[(i cos t + j sin t] = 2r(t). Нормальное ускорение направлено к центру окружности, о чем говорит знак «минус» ( r). Величина нормального ускорения равна an = 2r = . Это ускорение также называют центростремительным ускорением.

Если угловая скорость изменяется со временем, то имеем для скорости точки, вращающейся по окружности, r = r(icos + jsin ), v = . Вектор скорости v и в этом случае перпендикулярен радиус-вектору r, так как скалярное произведение данных векторов равно нулю (v,r) = 0. Величина линейной скорости определяется соотношением v =

произведение величины радиуса кривизны траектории в данной точке на угловую скорость вращения тела. полное ускорение точки, вращающейся с переменной угловой скоростью по окружности, по определению, равно Оно складывается из тангенциального ( = v/v) a = ( ) = r и нормального (n = r/r); ускорений.

Вектор a направлен по касательной к окружности – параллельно вектору v, а вектор an направлен к центру окружности – антипараллельно вектору r. Величина = (рад/с2) называется угловым ускорением и характеризует изменение угловой скорости в единицу времени. Определим величину нормального ускорения тела на экваторе, обусловленного вращением Земли. В данном случае угловая скорость вращения равна , где Т – период обращения Земли вокруг оси, Т = 1 сут = 8,64 104 с и R – радиус Земли, R = RЗ = = 6370 км. Подставляя данные значения T и R в формулу для нормального ускорения, получаем

Это всего лишь 0.35% от величины g = 9,8 м/с2. Таким образом, если бы Земля была идеально сферической, то на экваторе человек был бы на 0.35% легче, чем около полюса. Это одна из причин, объясняющих, почему в более высоких широтах труднее побить спортивные рекорды, чем на экваторе. Угловая скорость и угловое ускорение являются в общем случае векторами. Связь между вектором угловой и линейной скорости v задается с помощью векторного произведения v = [ ,r]. Вектор угловой скорости направлен перпендикулярно плоскости вращения, в сторону, определяемую правилом буравчика – если вращать буравчик по направлению движения точки, то его поступательное движение укажет направление вектора .

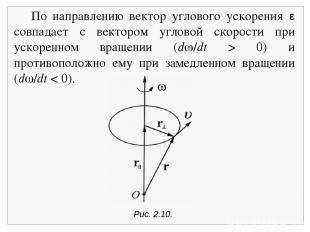
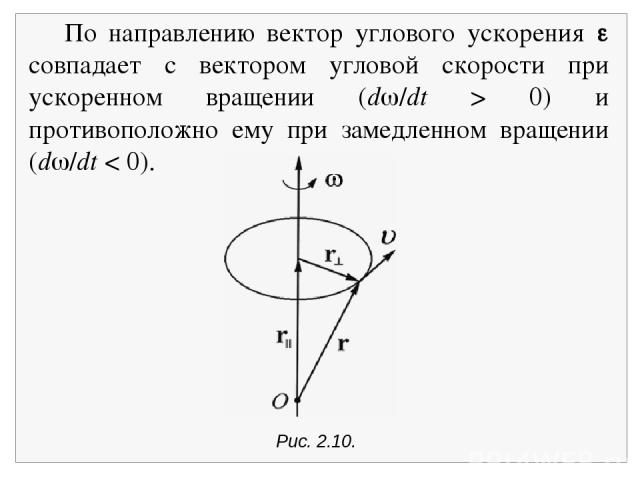
Рис. 2.10. По направлению вектор углового ускорения совпадает с вектором угловой скорости при ускоренном вращении (d /dt > 0) и противоположно ему при замедленном вращении (d /dt < 0).

Основные выводы r = r0 + vt Движение с постоянной скоростью описывается уравнением Мгновенная скорость v = Мгновенное ускорение а = Полное ускорение складывается из нормального an = n и тангенциального a = ускорений a = an + a .

Вектор угловой скорости угловое ускорение Связь между нормальным и тангенциальным ускорением и угловыми кинематическими характеристиками: an = 2rn, a = r . Прямая задача кинематики: по известному r=f(t) найти v,a=f(t). Обратная задача кинематики: по известному a=f(t) найти r=f(t).

Лекция окончена Нажмите клавишу для выхода