Презентация на тему: Новые преобразования для теории относительности

НОВЫЕ ПРЕОБРАЗОВАНИЯ ДЛЯ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ Томский политехнический университет г. Томск

Цель преобразований: Введение единых эталонов времени и протяженности для инерциальных систем отсчета (ИСО) S и S', двигающихся друг относительно друга со скоростью v

Противоречия и изъяны СТО, обнаруженные автором 1. Преобразования Лоренца (ПЛ) не удовлетворяют второму из трех векторных уравнений (3), соответствующих координатной записи эквивалентного уравнения (1) движения фронта световой волны, для двух геометрически диаметрально противоположных точек-событий

Противоречия и изъяны СТО, обнаруженные автором 2. При выводе ПЛ Эйнштейном было отброшено отрицательное значение функции (v), что скрыло истинный смысл преобразования одного связного множества (сферы t = const, определяемой уравнением (1)), в другое связное множество (вытянутый по оси X эллипсоид, который в получаемой деформированной системе S' отображается уравнением (2)).

Противоречия и изъяны СТО, обнаруженные автором 3. При налагаемых Эйнштейном требованиях линейной связи координат и времени координатная система S' получается однородным растяжением (гомотетией) вдоль оси X пространства координатной системы S в себя. При этом видно, что единица измерения протяженности (эталон протяженности) вдоль оси X' системы S' в k раз короче эталона протяженности, как по другим своим осям, так и единого эталона протяженности системы S.

Противоречия и изъяны СТО, обнаруженные автором 4. Идеальные часы Эйнштейна-Ланжевена, состоящие из пары параллельных зеркал, закрепленных на жестком стержне, в силу принципа относительности и разных эталонов протяженности в S' будут при изменении их ориентации показывать разное время. Кроме этого, совместное решение уравнений Это означает, что показания часов верны только при положении зеркал в плоскости

Противоречия и изъяны СТО, обнаруженные автором 5. Формулы преобразования скоростей в СТО при переходе от одной инерциальной системы к другой определяют не компоненты скорости произвольной материальной точки, а компоненты скорости точки светового фронта, т.к. преобразования Лоренца связывают не любые координаты и время двух ИСО, а координаты и время перемещения светового сигнала. Если определять относительную скорость материальной точки как отношение ее пути за время t' к пути, пройденному световым сигналом в том же направлении за тот же промежуток времени, то получим формулы, существенно отличающиеся от формул СТО:
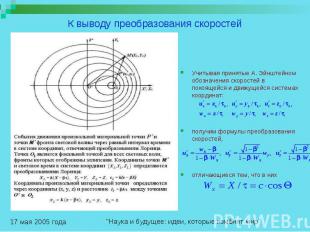
К выводу преобразования скоростей Учитывая принятые А. Эйнштейном обозначения скоростей в покоящейся и движущейся системах координат: получим формулы преобразования скоростей, отличающиеся тем, что в них

От преобразований Галилея и Лоренца к новым преобразованиям По сути, и преобразования Лоренца, и преобразования Галилея можно рассматривать как однотипные СК, образованные путем переноса начала координат в движущуюся относительно исходной системы точку. В преобразованиях Галилея определение новых координат производится тем же эталоном длины, а время принимается равным времени исходной системы. В результате этого путь эталонного движения в различных направлениях движущейся СК, при равенстве показаний часов, оказывается не одинаковым и, следовательно, скорость эталонного движения в ней не является константой. Отличие координатной системы преобразований Лоренца в том, что исходная СК деформируется и в ней рассматривается движущаяся СК. Новые координаты и время в преобразованиях Лоренца увязываются с путем эталонного движения так, что скорость эталонного движения в них является константой. Это приводит, как показано выше, к противоречиям и ошибкам. Однако, введя эквивалентность уравнений (1) и (2), А. Эйнштейн в специальной теории относительности заложил идею измерения времени одним движением или, другими словами, ввел одно эталонное движение для измерения времени в разных СК. При создании новых, свободных от противоречий СК и преобразований для определения их координат необходимо исходить из идеи Эйнштейна, сохраняя принцип одновременности событий в разных СК. При этом, однако, не следует забывать о высказывании А. Пуанкаре: «Никакая геометрия не может быть более истинна, чем другая; та или иная геометрия может быть только более удобной».
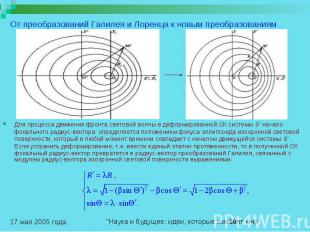
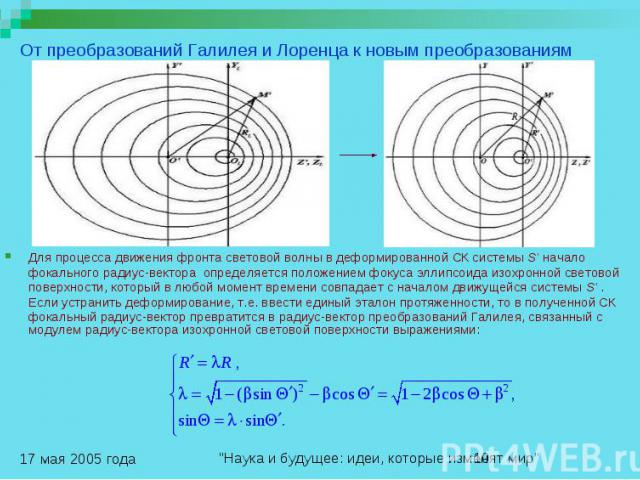
От преобразований Галилея и Лоренца к новым преобразованиям Для процесса движения фронта световой волны в деформированной СК системы S' начало фокального радиус-вектора определяется положением фокуса эллипсоида изохронной световой поверхности, который в любой момент времени совпадает с началом движущейся системы S' . Если устранить деформирование, т.е. ввести единый эталон протяженности, то в полученной СК фокальный радиус-вектор превратится в радиус-вектор преобразований Галилея, связанный с модулем радиус-вектора изохронной световой поверхности выражениями:

Эксцентрическая система координат Аналогами конических поверхностей с вершиной в начале координат будут служить поверхности, образованные вращением вокруг оси Z линий L, которые исходят из начала координат и в каждой своей точке перпендикулярны пересекаемым сферическим поверхностям, а касательные к ним в конечных точках направлены под углом . Эти кривые могут рассматриваться как криволинейные аналоги радиус-векторов полученной криволинейной СК, которую будем называть эксцентрической. Третьим семейством поверхностей, как и в обычной сферической СК, будут служить плоскости =const, проходящие через ось Z. Всем координатам и времени этой СК будем приписывать индекс «э», чтобы отличать их от координат и времени обычной сферической СК. Замечательно то, что координаты и время произвольной точки светового сигнала в этой движущейся эксцентрической СК равны координатам и времени исходной, «покоящейся» СК: Это обеспечивает как эквивалентность уравнений движения фронта световой волны (1,2), так и инвариантность любых законов в обеих ИСО. В то же время для определения эксцентрических координат наблюдателю, находящемуся в движущейся СК, придется вычислять их через обычные координаты сопутствующей сферической СК :
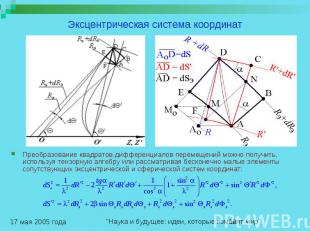
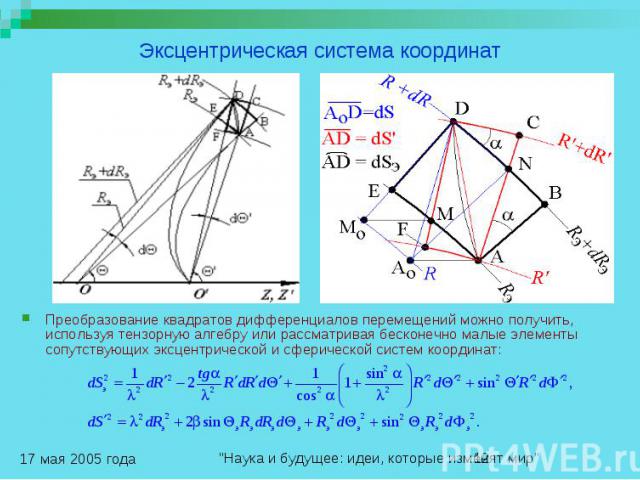
Эксцентрическая система координат Преобразование квадратов дифференциалов перемещений можно получить, используя тензорную алгебру или рассматривая бесконечно малые элементы сопутствующих эксцентрической и сферической систем координат:

Формулы для тензорных преобразований Для вычисления прочих дифференциальных соотношений эксцентрической СК через координаты сопутствующей сферической СК и обратно используются:

Использование эксцентрической системы координат Продуктивность использования эксцентрической СК покажем на следующем примере. Представим пространство в качестве материальной среды, в которой движутся материальные тела, отличающиеся от пространства своей внутренней структурой. Введем в пространстве евклидову метрику с единым эталоном протяженности и примем скорость передачи взаимодействия постоянной и равной по величине скорости света. В результате получим стационарное искривленное поле центральных сил, совпадающее с ЭСК, где окружности отвечают линиям постоянного потенциала, а перпендикулярные им линии L линиям тока, касательные к которым являются линиями сил, действующих в точках касания. Эксцентрические координаты при этом служат обобщенными координатами уравнения Лагранжа. Решая его для случая притяжения материальной точки, движущейся с сохранением полной энергии, получим формулу орбиты, которая в сопутствующей сферической СК имеет вид:
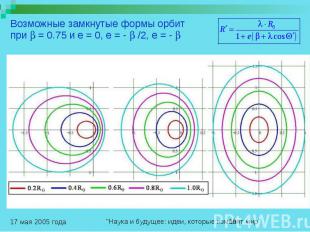
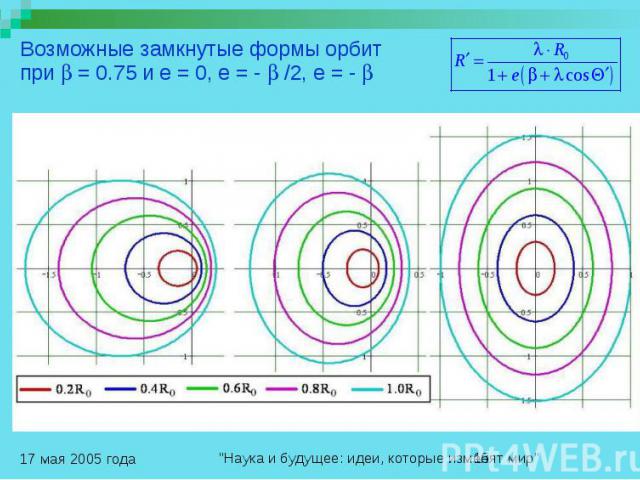
Возможные замкнутые формы орбит при = 0.75 и e = 0, e = - /2, e = -

Выводы по результатам расчета орбит в искривленном поле центральных сил Наиболее устойчивыми, с позиции законов симметрии, являются эллиптические орбиты с эксцентриситетом e = - , отношение размеров малых полуосей которых к большим полуосям соответствует кажущемуся сокращению размеров в СТО вдоль линии движения. Однако здесь, если материальными точками являются электроны, вращающиеся вокруг ядер, будет, во-первых, происходить не кажущееся, а реальное изменение размеров тела, во-вторых, размер тела в направлении движения остается неизменным, а увеличиваются в k раз поперечные размеры тела. При этом для наблюдателя, находящегося внутри данной СК, измеряемая им средняя скорость светового сигнала на пути туда и обратно в опытах, подобных опытам Майкельсона и Морли, будет величиной, не зависящей от направления, однако ее численное значение по сравнению со скоростью света в пространстве в k2 раз меньше. Кроме этого, преобразуя уравнения движения фронта световой волны выделением полного квадрата, мы получим те же самые преобразования Лоренца: которые приводят уравнение движения фронта световой волны в движущейся СК к виду, подобному исходному : Величину t ’ в преобразованиях Лоренца следует считать всего лишь приведенным временем перемещения светового сигнала в движущейся СК, где уравнение движения фронта световой волны имеет геометрически подобный вид. Использование этого подобия для определения частоты электромагнитного излучения, испускаемого движущимся источником, и дает известную формулу Эйнштейна, по которой рассчитывают эффект Доплера в различных направлениях. Его проверка в экспериментах, начиная с 1937 по 2003 года, дает все меньшее отклонение от формулы Эйнштейна.

О показаниях часов и времени Рассмотрим часы Эйнштейна-Ланжевена в движущейся СК при расстоянии между зеркалами l = 0,5: Время движения луча света от зеркала и обратно вдоль направления движения Время движения луча света от зеркала и обратно поперек направления движения Откуда видно, что часы Эйнштейна-Ланжевена при изменении их ориентации будут показывать одинаковое время, но в k2 раз меньше, чем такие же часы в покоящейся СК. Однако из этого не следует, что все процессы в движущейся СК будут протекать замедленно, т.к. время в обеих СК измеряется одним и тем же движением.

РЕЗЮМЕ В целом можно сделать вывод, что развитие идеи А.Эйнштейна об измерении времени одним движением в разных СК позволило создать новые, свободные от противоречий преобразования. В них сохраняется принцип одновременности событий, происходящих в разных системах отсчета, и инвариантность, как законов электродинамики, так и любых других законов, связанных с координатами и временем. Пример получения формулы орбит материальной точки в искривленном центральном поле сил показал продуктивность новых преобразований, т.к. в известных координатных системах решение уравнения Лагранжа приводит к эллиптическим интегралам. По преобразованиям Лоренца можно сделать вывод, что они дают формально верные результаты, как по исследованию изменения частоты, испускаемой движущимися атомами, так и по другим экспериментальным подтверждениям СТО, но их физическая и философская интерпретация, пожалуй, нуждается в пересмотре. Кроме этого, можно предположить, что новые преобразования, в которых используется специальная СК, названная эксцентрической, могут быть плодотворными при исследовании процессов, связанных с передачей взаимодействия через пространство. Дополнительным подтверждением данной теории, которой в будущем можно дать название эксцентрической теории взаимодействий, может служить полученный мною несколько лет назад объединенный дифференциальный закон взаимодействия тел с пространством и друг с другом, выведенный на основе простой модели также исходя из постулата о постоянстве скорости передачи взаимодействия в пространстве. Из этого закона: двукратным интегрированием получается второй закон Ньютона , с характером зависимости коэффициента k близким по форме к формуле Эйнштейна и начинающим отличаться по величине при > 0,4; четырехкратным интегрированием выводится закон всемирного тяготения. При этом отклонение от формулы Ньютона при отношении размера тел к расстоянию между ними R/l < 0,0005 не превышает 0,00003 % и возрастает до 21% при R/l =0,5. Эти результаты следует считать предварительными, т.к. вывод законов Ньютона производился без учета искривленности поля.