Презентация на тему: Интерференция света и её применение

Оптика Кафедра общей физики для студентов 2 курса ФТФ Авторы Светлана Алексеевна Чудинова, Ольга Яковлевна Березина [email protected] 900igr.net ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

Интерференция света Часть 2 Лекция 10 Условие пространственной когерентности Интерференция в тонких пленках Применение явлений интерференции ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

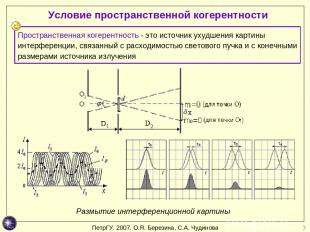
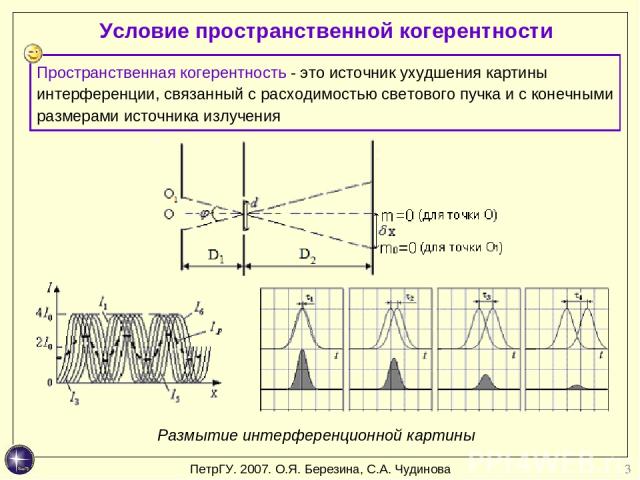
* Условие пространственной когерентности Размытие интерференционной картины Пространственная когерентность - это источник ухудшения картины интерференции, связанный с расходимостью светового пучка и с конечными размерами источника излучения ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

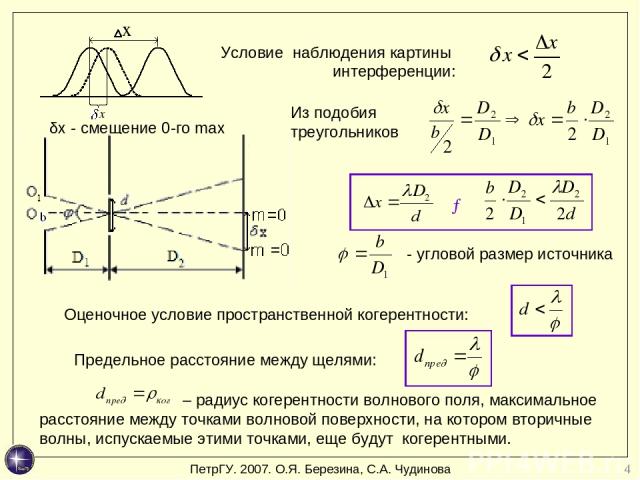
* δх - смещение 0-го max → - угловой размер источника Из подобия треугольников Условие наблюдения картины интерференции: Оценочное условие пространственной когерентности: Предельное расстояние между щелями: – радиус когерентности волнового поля, максимальное расстояние между точками волновой поверхности, на котором вторичные волны, испускаемые этими точками, еще будут когерентными. ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

* Пример При наблюдении картины интерференции от Солнца (его угловые размеры φ = 0,1 рад) для λ0 = 550 нм Объем когерентности - объединенное условие пространственной и временной когерентности ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

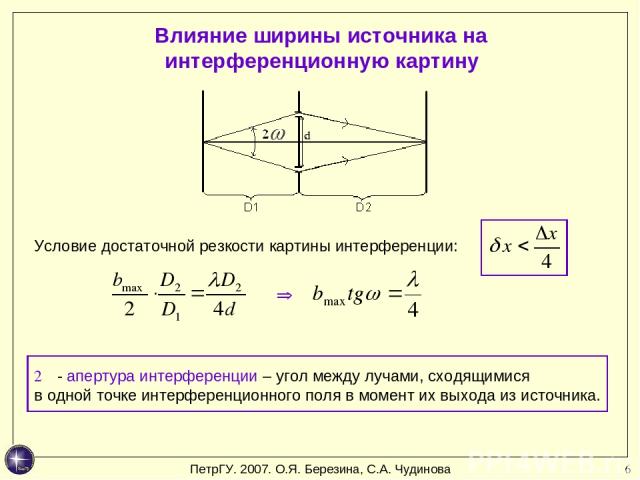
* Влияние ширины источника на интерференционную картину Условие достаточной резкости картины интерференции: 2ω - апертура интерференции – угол между лучами, сходящимися в одной точке интерференционного поля в момент их выхода из источника. ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

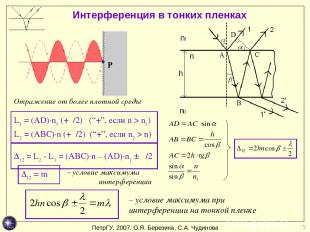
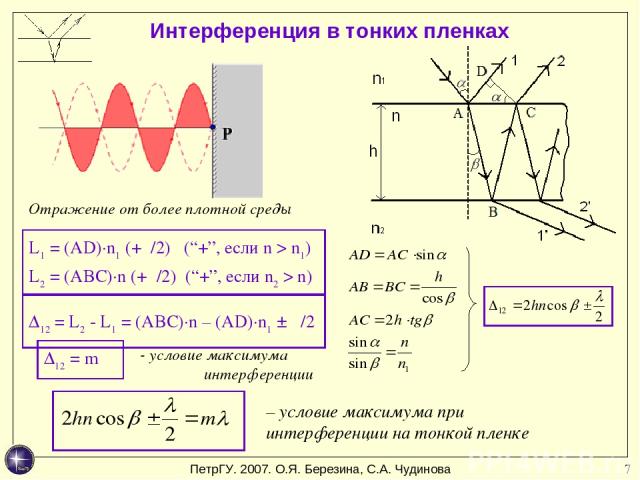
* Интерференция в тонких пленках Отражение от более плотной среды - условие максимума интерференции – условие максимума при интерференции на тонкой пленке L1 = (AD)·n1 (+λ/2) (“+”, если n > n1) L2 = (ABC)·n (+λ/2) (“+”, если n2 > n) ∆12 = L2 - L1 = (ABC)·n – (AD)·n1 ± λ/2 ∆12 = m λ ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

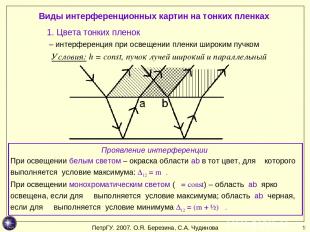
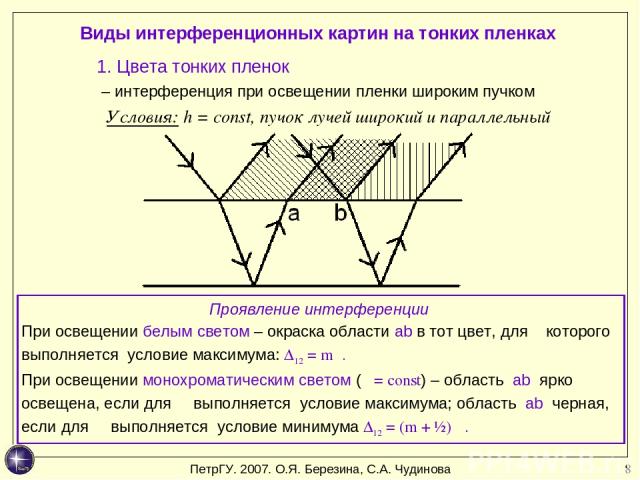
* Виды интерференционных картин на тонких пленках Условия: h = const, пучок лучей широкий и параллельный 1. Цвета тонких пленок – интерференция при освещении пленки широким пучком Проявление интерференции При освещении белым светом – окраска области ab в тот цвет, для λ которого выполняется условие максимума: ∆12 = mλ. При освещении монохроматическим светом (λ = const) – область ab ярко освещена, если для λ выполняется условие максимума; область ab черная, если для λ выполняется условие минимума ∆12 = (m + ½) λ. ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

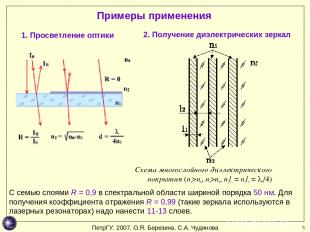
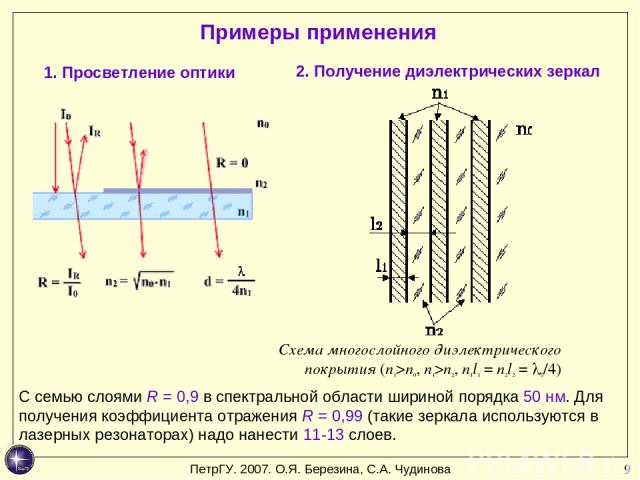
* Примеры применения 1. Просветление оптики 2. Получение диэлектрических зеркал Схема многослойного диэлектрического покрытия (n1>n0, n1>n2, n1l1 = n2l2 = l0/4) С семью слоями R = 0,9 в спектральной области шириной порядка 50 нм. Для получения коэффициента отражения R = 0,99 (такие зеркала используются в лазерных резонаторах) надо нанести 11-13 слоев. ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

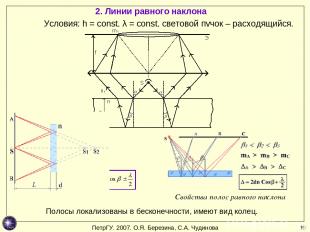
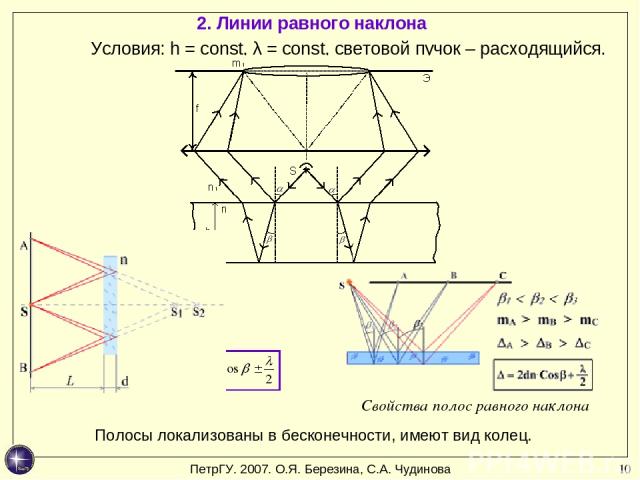
* 2. Линии равного наклона Условия: h = const, λ = const, световой пучок – расходящийся. Полосы локализованы в бесконечности, имеют вид колец. Свойства полос равного наклона ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

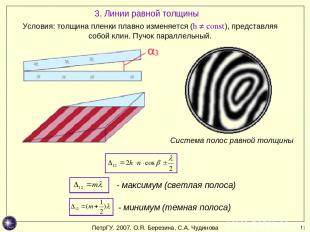
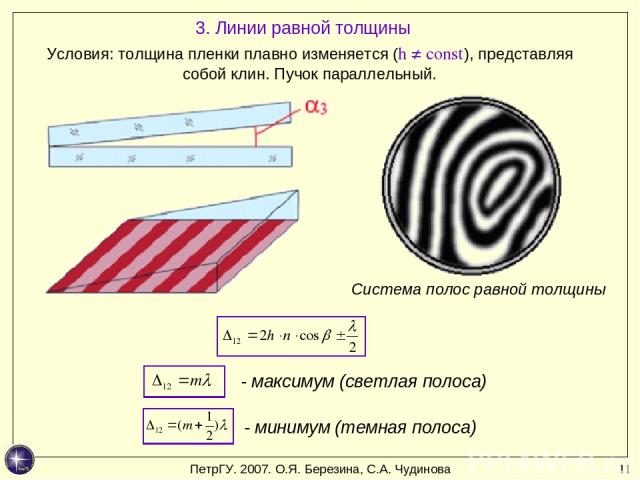
* 3. Линии равной толщины Условия: толщина пленки плавно изменяется (h ≠ const), представляя собой клин. Пучок параллельный. Система полос равной толщины - максимум (светлая полоса) - минимум (темная полоса) ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

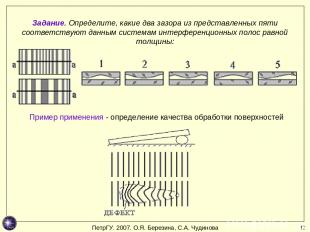
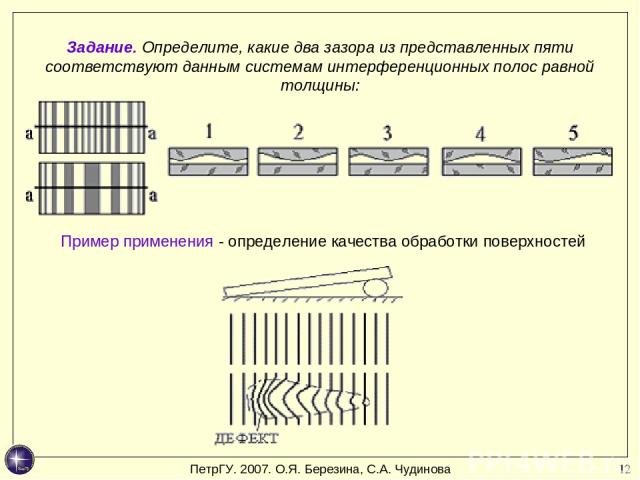
* Задание. Определите, какие два зазора из представленных пяти соответствуют данным системам интерференционных полос равной толщины: Пример применения - определение качества обработки поверхностей ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

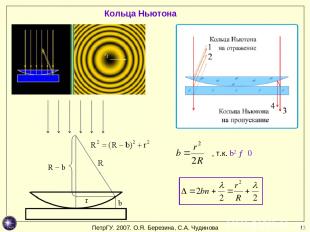
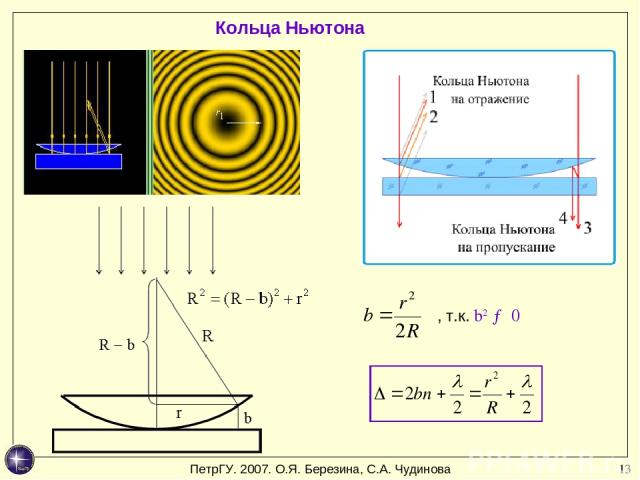
* Кольца Ньютона , т.к. b2 → 0 ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

* Условие максимума (светлые кольца) ∆ = m λ, где m – целое число. - радиус m-го светлого кольца в отраженном свете (и темного – в прошедшем) Условие минимума (темные кольца) ∆ = (m + ½) λ. - радиус m-го темного кольца в отраженном свете (и светлого – в прошедшем) Кольца Ньютона в зеленом и красном свете Пример применения – проверка качества шлифовки линз. ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

* Применение интерференции Для измерений: Длины волны λ Коэффициента преломления n Длин эталонов Малых перемещений Деформаций Качества обработки поверхностей ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

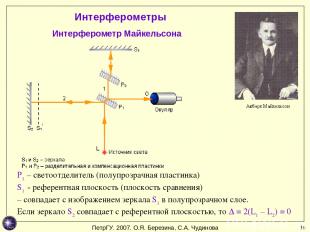
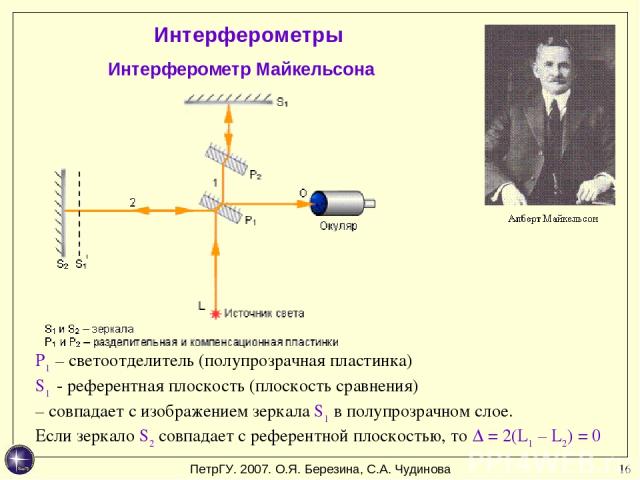
* Интерферометры Интерферометр Майкельсона P1 – светоотделитель (полупрозрачная пластинка) S1′- референтная плоскость (плоскость сравнения) – совпадает с изображением зеркала S1 в полупрозрачном слое. Если зеркало S2 совпадает с референтной плоскостью, то ∆ = 2(L1 – L2) = 0 ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

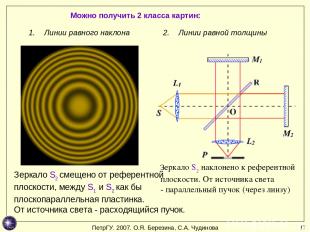
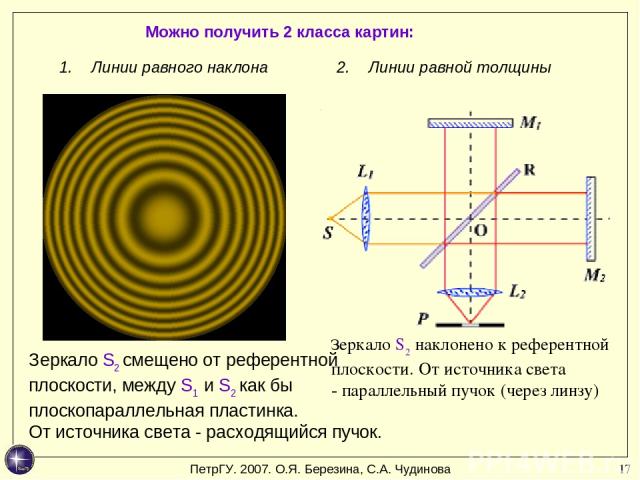
* Можно получить 2 класса картин: Зеркало S2 смещено от референтной плоскости, между S1 и S2 как бы плоскопараллельная пластинка. От источника света - расходящийся пучок. Зеркало S2 наклонено к референтной плоскости. От источника света - параллельный пучок (через линзу) Линии равного наклона Линии равной толщины ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

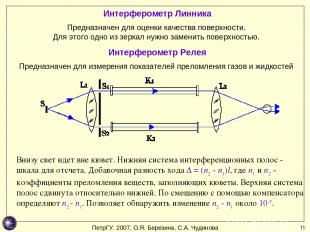
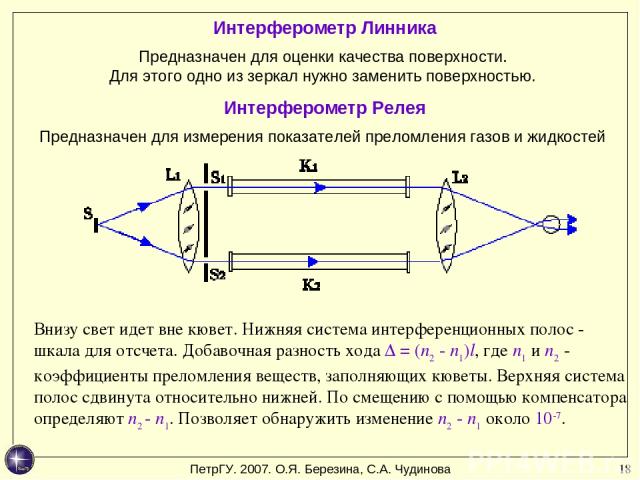
* Интерферометр Линника Предназначен для оценки качества поверхности. Для этого одно из зеркал нужно заменить поверхностью. Интерферометр Релея Предназначен для измерения показателей преломления газов и жидкостей Внизу свет идет вне кювет. Нижняя система интерференционных полос - шкала для отсчета. Добавочная разность хода ∆ = (n2 - n1)l, где n1 и n2 - коэффициенты преломления веществ, заполняющих кюветы. Верхняя система полос сдвинута относительно нижней. По смещению с помощью компенсатора определяют n2 - n1. Позволяет обнаружить изменение n2 - n1 около 10-7. ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

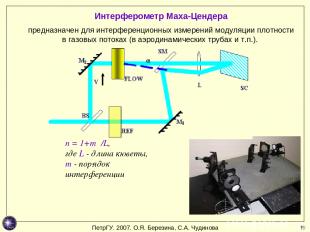
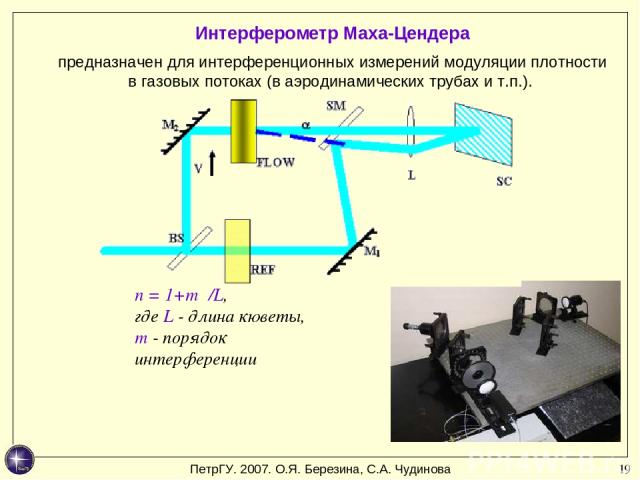
* Интерферометр Маха-Цендера предназначен для интерференционных измерений модуляции плотности в газовых потоках (в аэродинамических трубах и т.п.).  n = 1+mλ/L, где L - длина кюветы, m - порядок интерференции ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

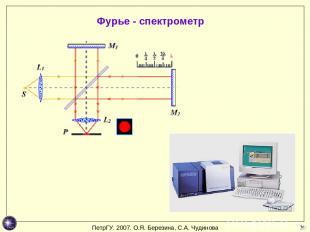
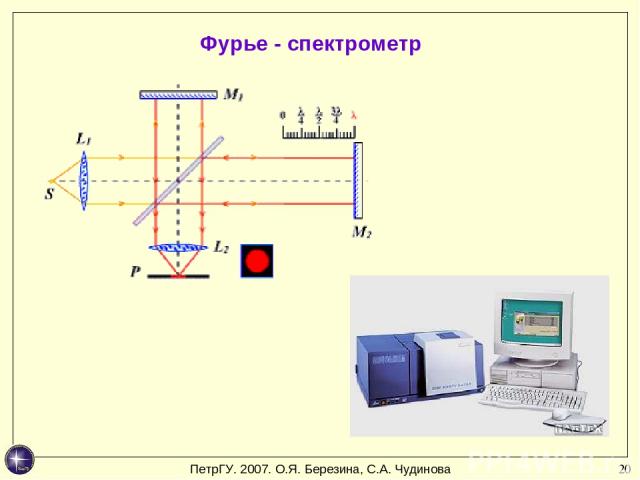
* Фурье - спектрометр ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова

* Продолжение следует ПетрГУ. 2007. О.Я. Березина, С.А. Чудинова