Презентация на тему: Импульс тела

Импульс

ОГЛАВЛЕНИЕ ИМПУЛЬС ТЕЛА ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА ТЕЛА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ Урок №1. Урок №2. Урок №3. ПРИМЕНЕНИЕ ЗАКОНА СОХРАНЕНИЯ ИМПУЛЬСА ТЕЛА

ИМПУЛЬС ТЕЛА Урок №1.

Причиной изменения скорости тела является действие на него силы F, при этом тело не может изменить свою скорость мгновенно. Выясним зависимость изменения скорости тела от силы действующей на него и времени действия этой силы при равноускоренном движении тела из состояния покоя : Следовательно, изменение скорости зависит не только от силы но и от времени ее действия

Согласно второму закону Ньютона: Ускорение тела при равноускоренном движении из состояния покоя равно: подставим вместо ускорения его значение и получим: Преобразуем данное выражение

Физическая величина, равная произведению силы, действующей на тело, и времени ее действия называется Физическая величина, равная произведению массы тела и его скорости называется импульс силы импульс тела Рассмотрим полученное выражение

Импульс тела – векторная физическая величина характеризующая количество движения. Направление вектора импульса тела совпадает с направлением скорости тела.

Если тело обладает скоростью, Если скорость тела равна нулю, то его импульс равен нулю, то его импульс не равен нулю,

Единицей измерения импульса в СИ является килограмм-метр в секунду

Понятие импульса было введено в физику французским ученым Рене Декартом (1596-1650). пример

Закон сохранения импульса Урок №2.

“Я принимаю, что во Вселенной, во всей созданной материи есть известное количество движения, которое никогда не увеличивается, не уменьшается, и, таким образом, если одно тело приводит в движение другое, то теряет столько своего движения, сколько его сообщает”. Рене Декарт. С другой стороны мы знаем третий закон Ньютона: Сила с которой взаимодействуют два любые тела, всегда равны по величине и противоположны по направлению.

Два этих утверждения не могут быть не взаимосвязаны так, как описывают одно и тоже взаимодействие. Докажем эту взаимосвязь. Согласно третьему закону Ньютона, силы взаимодействия между двумя телами равны: Умножим правую и левую части равенства на время взаимодействия. Получим в правой и левой части равенства импульсы сил которые сообщаются этим телам, а импульсы сил равны импульсам тел полученных во время их взаимодействия.

В более общем виде данное выражение выглядит следующим образом: При взаимодействии двух тел их общий импульс остается неизменным (т.е. сохраняется) Данный закон является фундаментальным законом природы. Закон сохранения импульса используется в случаях когда взаимодействие тел нельзя описать с помощью законов Ньютона, т. е. при долговременных или кратковременных взаимодействиях.

Для демонстрации закона сохранения импульса тела рассмотрим опыт. Подвесим на тонких нитях два одинаковых шарика Отведем один из шариков в сторону Мы видим что после столкновения левый шар остановился, а правый пришел в движение. Высота подъема правого шара, равна высоте на которую отклонили левый шар. Это говорит о том, что левыё шар отдал весь свой импульс правому шару. пример

Применение закона сохранения импульса Урок №3.

Закон сохранения импульса используется в случаях когда взаимодействие тел нельзя описать с помощью законов Ньютона, т. е. при долговременных или кратковременных взаимодействиях. Рассмотрим простой пример: возьмем детский резиновый шарик, надуем его и отпустим. Мы видим что когда воздух начинает выходить из шарика в одном направлении, то сам шарик полетит в другую сторону Движение тела, возникающее при отделении от тела его части с некоторой скоростью, называется реактивным движением.

Рассмотрим реактивное движение с помощью закона сохранения импульса Следовательно импульсы тел, до взаимодействия, тоже равны нулю Скорость шарика в начальный момент времени была равна нулю И скорость воздуха в начальный момент времени была равна нулю

Предположим, что воздух выходит из шарика с одинаковой скоростью После выхода всего газа массой m2 , шар приобретет скорость Тогда импульсы тел после взаимодействия будут равны: Согласно закону сохранения импульса, получим:

Найдем скорость шарика Знак «-» показывает, что скорость шарика имеет противоположное направление скорости вырывающегося из него воздуха.

Реактивное движение, возникающее при выбросе воды, можно наблюдать на следующем опыте. Нальем воду в стеклянную во ронку, соединенную с резиновой трубкой, имеющей Г-образный наконечник. Мы увидим, что, когда вода начнет выли ваться из трубки, сама трубка придет в движение и отклонится в сторону, противоположную направлению вытекания воды.

По принципу реактивного движения передвигаются некоторые представители животного мира, например кальмары и осьминоги. Периодически выбрасывая вбираемую в себя воду, они способны развивать скорость до 60—70 км/ч. Аналогичным образом пере мещаются медузы, каракатицы и некоторые другие животные. Примеры реактивного движения можно обнаружить и в мире растений. Например, созревшие плоды «бешеного» огурца при самом легком прикосновении отскакивают от плодоножки и из отверстия, образовавшегося на месте отделившейся ножки, с силой выбрасывается горькая жидкость с семенами; сами огурцы при этом отлетают в противоположном направлении.

На принципе реактивного движения основаны полеты ракет. Современная космическая ракета представляет собой очень сложный летательный аппарат, состоящий из сотен тысяч и миллионов деталей. Масса ракеты огромна. Она складывается из массы рабочего тела (т. е. раскаленных газов, образующихся в результате сгорания топлива и выбрасываемых в виде реактивной струи) и конечной или, как говорят, «сухой» массы ракеты, остающейся после выброса из ракеты рабочего тела.

Обозначим «сухую» массу ракета Скорость ракеты а массу вырывающихся газов Скорость вырывающихся газов То уравнение полученное нами для резинового шарика примет следующий вид

Мы видим, что чем больше масса ракеты тем меньше ее скорость. По мере истечения рабочего тела освободившиеся баки, лишние части оболочки и т. д. начинают обременять ракету ненужным грузом, затрудняя ее разгон. Поэтому для достижения космических скоростей применяют составные (или многоступенчатые) ракеты. Сначала в таких ракетах работают лишь блоки первой ступени 1. Когда запасы топлива в них кончаются, они отделяются и включается вторая ступень 2; после исчерпания в ней топлива она также отделяется и включается третья ступень 3. Находящийся в головной части ракеты спут ник или какой-либо другой космический аппарат укрыт головным обтекателем 4, обтекаемая форма которого способствует уменьшению сопротивления воздуха при по лете ракеты в атмосфере Земли. 1 2 3 4

Формула выведенная нами является приближенной. В ней не учитывается, что по мере сгорания топлива масса летящей ракеты становится все меньше и меньше. Точная формула для скорости ракеты впервые была получена в 1897 г. К. Э. Циолковским. В таблице приведены отношения начальной массы ракеты к ее конечной массе , соответствующие разным скоростям ракеты при скорости газовой струи (относи тельно ракеты) т0/т т0/т т0/т 4 8 12 2,7 7,4 20,1 16 20 24 55 148 403 28 32 36 1100 2980 8100

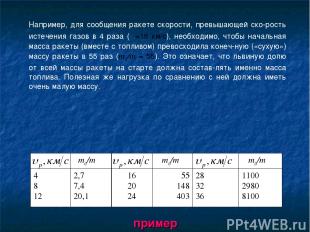
Например, для сообщения ракете скорости, превышающей ско рость истечения газов в 4 раза (υ=16 км/с), необходимо, чтобы начальная масса ракеты (вместе с топливом) превосходила конеч ную («сухую») массу ракеты в 55 раз (т0/т = 55). Это означает, что львиную долю от всей массы ракеты на старте должна состав лять именно масса топлива. Полезная же нагрузка по сравнению с ней должна иметь очень малую массу. пример т0/т т0/т т0/т 4 8 12 2,7 7,4 20,1 16 20 24 55 148 403 28 32 36 1100 2980 8100

Примеры решения задач. Импульс тела Закон сохранения импульса тела В оглавление Реактивное движение

Чему равен импульс космического корабля, движущегося со скоростью 8 км/с? Масса корабля 6,6 т. Дано: Решение: СИ Ответ:

Когда человек подпрыгивает, то, отталкивается ногами от земного шара, он сообщает ему некоторую скорость. Определите эту скорость, если масса человека 60 кг и он отталкивается со скоростью 4,4 м/с. Масса земного шара 6*1024 кг. Дано: Решение: Ответ: Рассмотрим импульсы человека и земли до взаимодействия: После взаимодействия импульсы человека и земли станут равны: Согласно закону сохранения импульса, полный импульс системы остается неизменным: следовательно: Знак «-» показывает, что скорость земного шара имеет противоположное направление скорости человека.

Чему равна скорость пороховой ракеты массой 1 кг после вылета из нее продуктов сгорания массой 0,1 кг со скоростью 500 м/с. Дано: Решение: Ответ: Рассмотрим импульсы ракеты и продуктов сгорания до взаимодействия: После взаимодействия импульсы ракеты и продуктов сгорания станут равны: следовательно: Знак «-» показывает, что скорость земного шара имеет противоположное направление скорости человека. Согласно закону сохранения импульса, полный импульс системы остается неизменным: