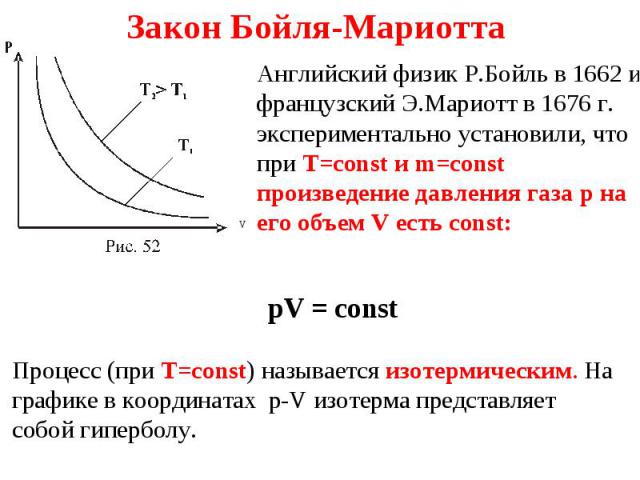
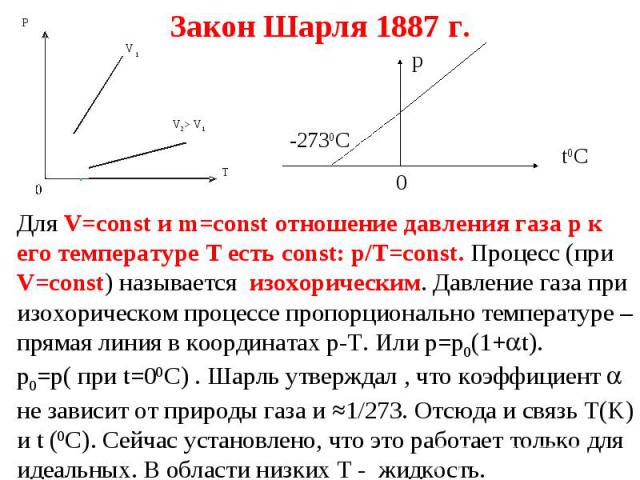
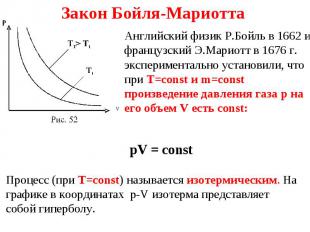
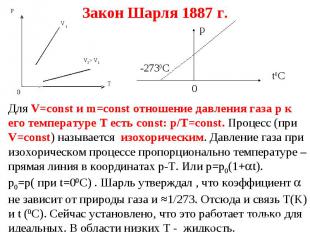
Презентация на тему: 11 Основные положения, идеальный газ

Левкит и Демокрит (379 г. до н.э.) – вещество из атомов (от греческого слова неделимый). Левкит и Демокрит (379 г. до н.э.) – вещество из атомов (от греческого слова неделимый). Теория теплорода – невидимое и невесомое вещество которое входит и выходит из тела при нагреве и охлаждении. Существовала до 18-19 в.в. но такие термины как количество теплоты, теплоемкость используются до сих пор. Ломоносов (1711-1765): тепловые явления необходимо объяснять движением и взаимодействием молекул. Впервые ввел деление на молекулы и атомы. Говорил о корпускулах .

Микроскопический подход – изучает молекулы и их малые совокупности. Использует законы механики для отдельных М. Законы механики необходимы, но недостаточны. Но для большого количества молекул возникают принципиально новые закономерности , которые не работают для малого числа молекул. Для их описания и разработаны статистические методы которые развиваются в макроскопическом подходе. Микроскопический подход – изучает молекулы и их малые совокупности. Использует законы механики для отдельных М. Законы механики необходимы, но недостаточны. Но для большого количества молекул возникают принципиально новые закономерности , которые не работают для малого числа молекул. Для их описания и разработаны статистические методы которые развиваются в макроскопическом подходе. Макроскопический подход – описывает большие совокупности М (термодинамика и статистическая физика) . Статистическая физика описывает свойства макросистем (температуру и давление ) как усредненный (суммарный) результат действия всех молекул. Она интересуется не движением отдельных молекул, а лишь средними величинами, которые характеризуют движение огромной совокупности частиц.

Ланжевен предложил уравнение, описывающее движение броуновской частицы с учетом соударений частиц Ланжевен предложил уравнение, описывающее движение броуновской частицы с учетом соударений частиц γ- вязкость. Уравнение используется для изучения флуктуаций молекул в системах, включая неравновесную термодинамику

Как «услышать» микромир? Используем уже упоминавшийся ранее лазерный пинцет! Лазерный пинцет может удерживать объекты микромира и манипулировать ими. Объекты притягиваются к лазерному лучу, взаимодействуя с создаваемым им электрическим полем. Авторы использовали несколько лучей которые окружали кольцом молекулу. Как «услышать» микромир? Используем уже упоминавшийся ранее лазерный пинцет! Лазерный пинцет может удерживать объекты микромира и манипулировать ими. Объекты притягиваются к лазерному лучу, взаимодействуя с создаваемым им электрическим полем. Авторы использовали несколько лучей которые окружали кольцом молекулу. Звуковые волны, исходящие от объекта, воздействовали на проходящие сквозь толщу воды лучи. Камеры фиксировали изменения лучей. Анализируя информации помог восстановить издаваемые объектами звуки. Авторам удалось записать звуки, производимые при броуновском движении объектов. В будущем исследователи не исключают, что с помощью новой технологии они смогут услышать, какие звуки издают бактериальные клетки при воздействии лекарственных препаратов.

В нормальных условиях t=0o C и p=1атм=10,1·104 Па объем моля идеального газа Vмоля=RT/p=22,4 л/моль = (2 ведра/моль)=2,24·10-2 м3/моль, Число молекул в 1 м3–число Лошмидта NL=NA/Vмоля=2.69 1025 м-3 В нормальных условиях t=0o C и p=1атм=10,1·104 Па объем моля идеального газа Vмоля=RT/p=22,4 л/моль = (2 ведра/моль)=2,24·10-2 м3/моль, Число молекул в 1 м3–число Лошмидта NL=NA/Vмоля=2.69 1025 м-3 Относительная атомная масса А: отношение массы атома m к 1/12 массе атома 12С: А=Мотн=m/(mC/12). Молярная масса (масса одного моля)- масса вещества в количестве один моль μ=NAm=NAA mC/12=A mмоля С /12=А 0,012/12=А 10-3 кг/моль=А г/моль. Т.е. когда мы видим в таблице Менделеева А оно численно равно массе одного моля данного вещества в граммах . Чему равна молярная масса? Относительная масса всех химических элементов складывается из относительных масс атомов. 2H+1O => A=2x1.0079 +15.999≈18 => μH2O≈18 г/моль. Моль железа весит 55,847 г и занимает Vмоль Fe=7.09 см3(≈ одна столовая железная ложка!)

Температура – степень нагретости. Как измерить? Ведь эталона нет и => используем принцип теплового равновесия. Т.е. предоставляем две системы , находящиеся в тепловом контакте сами себе. Со временем они придут в состояние теплового равновесия и => их температуры равны. Чтобы измерить давайте одно из тел используем в качестве термометра. Температура связана с изменением средней скорости молекул , а сама температура прямо пропорциональна средней кинетической энергии Температура – степень нагретости. Как измерить? Ведь эталона нет и => используем принцип теплового равновесия. Т.е. предоставляем две системы , находящиеся в тепловом контакте сами себе. Со временем они придут в состояние теплового равновесия и => их температуры равны. Чтобы измерить давайте одно из тел используем в качестве термометра. Температура связана с изменением средней скорости молекул , а сама температура прямо пропорциональна средней кинетической энергии Шкалы: Цельсия (при атмосферном давлении интервал между точками таяния льда и кипения воды разделен на 100 частей . Точка таяния льда взята за 00С а кипения 1000С. Фаренгейта (интервал между точками таяния льда и кипения воды разделен на 180 частей . Точка таяния льда взята за 320F а кипения 2120F , t0С= 5(t0F-320F)/9 Кельвина: t0С=(T-273,15)0K. C большой точностью совпадает со шкалой Цельсия 1С=1К. Названа в честь английского физика У. Томсона – лорда Кельвина, предложившего принцип организации температурной шкалы на основе второго начала термодинамики.

Физикам удалось экспериментально подтвердить для броуновских частиц известную теорему о равнораспределении кинетической энергии по степеням свободы (вернемся к ней позже). Теорема о равнораспределении кинетической энергии по степеням свободы связывает температуру системы и ее среднюю энергию. Для определения энергии частицы достаточно знать ее массу и скорость. Однако броуновские частицы слишком часто меняют направление и скорость своего движения. Ученые опять применили лазерный луч для исследования маленьких стеклянных шариков, плавающих в воздухе (столкновения частиц происходят реже чем в воде). Если определить параметры отражения частицами лазерного луча до того, как происходили столкновения и смогли оценить скорость движения частиц и определить их энергию. Физикам удалось экспериментально подтвердить для броуновских частиц известную теорему о равнораспределении кинетической энергии по степеням свободы (вернемся к ней позже). Теорема о равнораспределении кинетической энергии по степеням свободы связывает температуру системы и ее среднюю энергию. Для определения энергии частицы достаточно знать ее массу и скорость. Однако броуновские частицы слишком часто меняют направление и скорость своего движения. Ученые опять применили лазерный луч для исследования маленьких стеклянных шариков, плавающих в воздухе (столкновения частиц происходят реже чем в воде). Если определить параметры отражения частицами лазерного луча до того, как происходили столкновения и смогли оценить скорость движения частиц и определить их энергию.