Презентация на тему: 10 Волны

Если колебания совершаются с одной частотой ω , но с разными фазами и амплитудами. Если колебания совершаются с одной частотой ω , но с разными фазами и амплитудами. Если колебания совершаются в фазе то есть φ2–φ1=2πn, где n – целое число, включая нуль, то cos(φ2–φ1) = 1 и амплитуды колебаний просто складываются: A=A1+A2 Если же колебания происходят в противофазе, то есть φ2 – φ1= (2n+1)π, то cos(φ2–φ1)=–1 и A = |A1 – A2| В обоих случаях гармонические колебания

Обозначим и . Тогда Обозначим и . Тогда x = (2AcosΩt)sinωt Результат сложения колебаний представляет собой произведение двух периодических (и гармонических) функций с сильно различающимися частотами Ω и ω: Ω « ω. Данное колебание, строго говоря, не является гармоническим, так как при гармоническом колебании амплитуда постоянна. Но его можно рассматривать как гармоническое колебание с амплитудой, изменяющейся по закону cos. Такие колебания называют биениями.

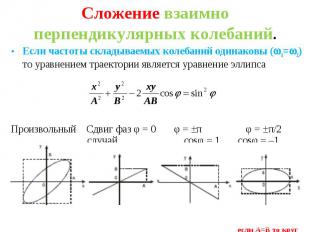
Если частоты складываемых колебаний одинаковы ( 1= 2) то уравнением траектории является уравнение эллипса Если частоты складываемых колебаний одинаковы ( 1= 2) то уравнением траектории является уравнение эллипса Произвольный Сдвиг фаз φ = 0 φ = ±π φ = ±π/2 случай сosφ = 1 cosφ = –1 cosφ = 0 если А=В то круг

Если отношение частот ω1 и ω2 равно отношению целых чисел m/n (т.е. рациональное число по определению), то траектория результирующего движения представляет собой замкнутую фигуру, называемую фигурой Лиссажу Если отношение частот ω1 и ω2 равно отношению целых чисел m/n (т.е. рациональное число по определению), то траектория результирующего движения представляет собой замкнутую фигуру, называемую фигурой Лиссажу Предыдущие фигуры являются простейшим частным случаем фигур Лиссажу, когда m=n. На рисунках приведены еще два случая для отношения частот 1:2 и 3:2. Если же отношение частот является иррациональным числом (те действительным но не рациональным ), то траектория точки не будет замкнутой, она будет проходить через все новые и новые точки внутри прямоугольника, стремясь заполнить его целиком. Траектория уже не фигура, а бесконечная кривая в конечном прямоугольнике

Причиной возникновения волны в любое среде является отклонение значения давления от исходного. Если данное отклонение периодически повторяется, то возникает стационарная волна. Причиной возникновения волны в любое среде является отклонение значения давления от исходного. Если данное отклонение периодически повторяется, то возникает стационарная волна. Всякое изменение давления (а следовательно и плотности среды) передается с определенной скоростью соседним частицам. Это и есть скорость распространения волны Волновой фронт (поверхность) – поверхность на которой фаза колебаний всех атомов и молекул в данный момент времени одинакова (плоскость, круг, сфера). Волна распространяется по нормали к волновому фронту. Простейшие случаи волновых поверхностей: Круговые волны: возмущение распложено по кругу (от падения камня в воду). Сферические волны: возмущение распложено по сфере (звуковая волна от сферического громкоговорителя в однородной среде)

Поляризация описывает характер расположения возмущения вдоль направления распространения волны (анизотропию характеристик волны в плоскости, перпендикулярной к направлению ее распространения). Поляризация описывает характер расположения возмущения вдоль направления распространения волны (анизотропию характеристик волны в плоскости, перпендикулярной к направлению ее распространения). Поперечную волну называют плоско или линейно поляризованной если волновые поверхности представляют собой набор параллельных плоскостей. Пример: Плоско поляризованная упругая волна начнет распространяться вдоль резиновой трубки если будем перемещать ее конец строго в одном направлении (например, вертикально) перпендикулярно длине трубки (т.е. все отклонения в перпендикулярной плоскости). Если направление перемещения конца трубки крутить то и волна выйдет из данной плоскости. Посмотрим опыт.

Если пренебречь потерями энергии (например, на нагрев шланга и возбуждение волн в воздухе ) то мы видим , что возмущение распространяется по резиновой трубке без искажений или возникает бегущая волна. Ее можно описать как Если пренебречь потерями энергии (например, на нагрев шланга и возбуждение волн в воздухе ) то мы видим , что возмущение распространяется по резиновой трубке без искажений или возникает бегущая волна. Ее можно описать как где y(х,t) отклонение (возмущение) частицы струны с координатой x в момент времени t. Можно показать, что волна любой формы представленная f , распространяется со скоростью v. Верно для любой плоской волны вдоль x. Вид аргумента функции (х-vt) –признак бегущей волны. В струне где N- натяжение, ρ –линейная плотность. Верно для абсолютно гибкой струны. Кто играет на гитаре ? и

Групповая скорость- скорость движения группы или цуга длин волн, образующихся в данный момент времени локализованных в пространстве в волновой пакет ( например, набор гармонических волн с частотой в определенном диапазоне). Если групповая скорость отлична от нуля то есть перенос энергии и импульса. Групповая скорость- скорость движения группы или цуга длин волн, образующихся в данный момент времени локализованных в пространстве в волновой пакет ( например, набор гармонических волн с частотой в определенном диапазоне). Если групповая скорость отлична от нуля то есть перенос энергии и импульса. Фазовая скорость-скорость перемещения фазы волны в определенном направлении. Групповая совпадает с фазовой если нет дисперсии (зависимости показателя преломления среды от длины волны) . Принцип суперпозиции – волны просто накладываются друг на друга (складываются) не возмущая друг друга. На практике возможны и нелинейные эффекты. Пример: параметрическое резонансное усиление в «волне убийце» высотой до 25-30 м. Возможен ли такой процесс в атмосфере? Каковы значения максимального и минимального давления и температуры? Из принципа суперпозиции следует две одинаковые встречные волны образуют стоячую волну (на практике возникают при отражении от препятствия).

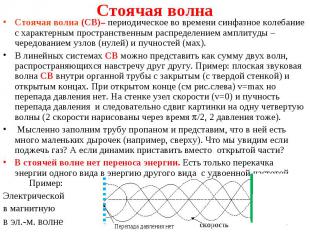
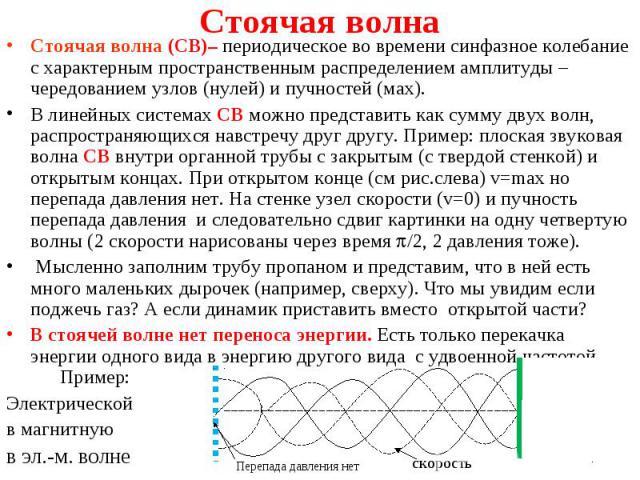
Стоячая волна (СВ)– периодическое во времени синфазное колебание с характерным пространственным распределением амплитуды – чередованием узлов (нулей) и пучностей (мах). Стоячая волна (СВ)– периодическое во времени синфазное колебание с характерным пространственным распределением амплитуды – чередованием узлов (нулей) и пучностей (мах). В линейных системах СВ можно представить как сумму двух волн, распространяющихся навстречу друг другу. Пример: плоская звуковая волна СВ внутри органной трубы с закрытым (с твердой стенкой) и открытым концах. При открытом конце (см рис.слева) v=max но перепада давления нет. На стенке узел скорости (v=0) и пучность перепада давления и следовательно сдвиг картинки на одну четвертую волны (2 скорости нарисованы через время /2, 2 давления тоже). Мысленно заполним трубу пропаном и представим, что в ней есть много маленьких дырочек (например, сверху). Что мы увидим если поджечь газ? А если динамик приставить вместо открытой части? В стоячей волне нет переноса энергии. Есть только перекачка энергии одного вида в энергию другого вида с удвоенной частотой. Пример: Электрической в магнитную в эл.-м. волне

Звуковыми волнами называются упругие волны в любой среде с частотой от 16 Гц до 20 кГц (т.е. то , что может воспринять человеческое ухо) Звуковыми волнами называются упругие волны в любой среде с частотой от 16 Гц до 20 кГц (т.е. то , что может воспринять человеческое ухо) Волны с частотой меньше 16 Гц называются инфразвуком, выше 20 кГц — ультразвуком. Хотя инфразвуки человек и не слышит, но воспринимает (некоторые частоты близки к собственным частотам колебаний некоторых человеческих органов («слышит» не ухом, а телом)). При достаточно большой мощности таких инфразвуков происходит резонанс и последствия могут оказаться крайне нежелательными. Дети могут слышат ультразвук. С возрастам соотв. ворсинки отмирают первыми. Можно отпугивать хулиганов Всякий реальный звук представляет собой не простое гармоническое колебание, а является наложением гармонических колебаний с определенным набором частот - теорема Фурье.

произвольный, периодический во времени физический процесс с частотой , описываемый функцией х(t), может быть представлен в виде суперпозиции бесконечного числа гармонических колебаний, частоты которых образуют дискретную последовательность: произвольный, периодический во времени физический процесс с частотой , описываемый функцией х(t), может быть представлен в виде суперпозиции бесконечного числа гармонических колебаний, частоты которых образуют дискретную последовательность: Наименьшая частота этого ряда Фурье равна частоте периодического процесса . Эта частота называется основным тоном звука (первая гармоника). Остальные частоты гармонического ряда, кратные (то есть n , где n — целые числа), называются обертонами. Коэффициенты Аn , являющиеся амплитудами соответствующих гармонических составляющих. А0-среднее значение функции.

Набор частот колебаний, присутствующих в данном звуке - акустический спектр. Звуки всех музыкальных инструментов имеют линейчатый акустический спектр. Если одну Набор частот колебаний, присутствующих в данном звуке - акустический спектр. Звуки всех музыкальных инструментов имеют линейчатый акустический спектр. Если одну

Струнные смычковые музыкальные инструменты имеют не слишком широкий диапазон издаваемых звуковых тонов: Струнные смычковые музыкальные инструменты имеют не слишком широкий диапазон издаваемых звуковых тонов: Скрипка — от 196 до 2000 Гц; Альт — от 131 до 1100 Гц; Виолончель — от 65 до 700 Гц; Контрабас — от 41 до 240 Гц. Орган – от 1 до 32 футов. 74? Однако, поскольку они имеют широкий спектральный состав, то при записи и последующем воспроизведении этих звуков необходимо пользоваться усилителями и динамиками, способными работать в линейном режиме с широким диапазоном частот (чтобы не исказить отдельные обертона и сохранить тембр звуков). При изготовлении инструмента мастер старается сделать так, чтобы сделать наилучшую окраску звука ( а фактически за счет использования различных пород дерева, лаков и формы подобрать необходимый спектр).

Существуют звуки, в которых присутствуют колебания всех частот в некотором интервале от 1 до 2. Такой звук называется шумом, а его акустический спектр является сплошным. Существуют звуки, в которых присутствуют колебания всех частот в некотором интервале от 1 до 2. Такой звук называется шумом, а его акустический спектр является сплошным.

Человек слышит звук не любой интенсивности. Ухо таково, что услышать звук оно может, только если интенсивность превысит некоторую минимальную величину, называемую порогом слышимости. Порог слышимости зависит от частоты звука: наиболее высокая чувствительность наблюдается в районе 3 кГц. Порог слышимости при этом составляет в среднем (усреднение по многим людям) 10-12 Вт/м2. Человек слышит звук не любой интенсивности. Ухо таково, что услышать звук оно может, только если интенсивность превысит некоторую минимальную величину, называемую порогом слышимости. Порог слышимости зависит от частоты звука: наиболее высокая чувствительность наблюдается в районе 3 кГц. Порог слышимости при этом составляет в среднем (усреднение по многим людям) 10-12 Вт/м2. Почему максимальная чувствительность находится в районе 3 кГц? Объяснение чисто физическое – все дело в резонансе столбика воздуха в человеческом ушном канале. Ушной канал представляет собой закрытую с одной стороны барабанной перепонкой акустическую трубку длиной примерно 2.7 см. Столбик воздуха внутри такого ушного канала резонирует на звук с длиной волны, равной четырем его длинам, что и соответствует 3 кГц.

При интенсивности 1-10 Вт/м2 человек чувствует боль и эти интенсивности называются порогом болевого ощущения. Есть специальные устройства направленного действия (плоские магнитные динамики) для разгона демонстраций. Т.е. простой инструмент который всегда с нами –ухо воспринимает 12-13 порядков величины. Между двумя порогами пользуются понятием громкости звука. Уровнем громкости L в технике называют логарифм отношения интенсивности данного звука I к начальной интенсивности I0: При интенсивности 1-10 Вт/м2 человек чувствует боль и эти интенсивности называются порогом болевого ощущения. Есть специальные устройства направленного действия (плоские магнитные динамики) для разгона демонстраций. Т.е. простой инструмент который всегда с нами –ухо воспринимает 12-13 порядков величины. Между двумя порогами пользуются понятием громкости звука. Уровнем громкости L в технике называют логарифм отношения интенсивности данного звука I к начальной интенсивности I0: за I0 - принимают порог слышимости при 1000 Гц. Единица уровня громкости называется бел (Б). Удобней пользоваться в 10 раз меньшей единицей – децибелом (дБ). 1Б=10дБ. Громкость в децибелах находится по формуле:

Для примера: Для примера: Тикание часов -20 дБ Шепот на 1 метре – 30 дБ Тихий разговор – 40 дБ Громкой речь, а также допустимый уровень шума строительных работах в ночное время – 70 дБ Крик – 80 дБ, Шум двигателя самолета на 5 (3) метрах – 120(130) дБ Отличие в дБ в 6 раз а реально на 10 порядков величины!!!!

Пусть T0=λ0/v0=1/ν0 период между импульсами испускаемыми неподвижным источником (λ0 - расстояние между двумя импульсами) . До неподвижного наблюдателя импульсы так и будут доходить с периодом Т0. Если же источник звука начнет двигаться со скоростью vд (полагаем пока, что vд<v0) к наблюдателю, то импульсу надо пройти меньший путь на расстояние vдT0 , которое проходит источник за период T0 и соседние импульсы будут разделены меньшим промежутком времени: Пусть T0=λ0/v0=1/ν0 период между импульсами испускаемыми неподвижным источником (λ0 - расстояние между двумя импульсами) . До неподвижного наблюдателя импульсы так и будут доходить с периодом Т0. Если же источник звука начнет двигаться со скоростью vд (полагаем пока, что vд<v0) к наблюдателю, то импульсу надо пройти меньший путь на расстояние vдT0 , которое проходит источник за период T0 и соседние импульсы будут разделены меньшим промежутком времени: λд=λ0–vдT0=λ0–vд/ν0=vд/νд или νд=ν0/(1-vд/v0) Если источник удаляется от наблюдателя, то длина волны и частота увеличивается на ту же величину: λд=λ0+vд/ν0 или νд= ν 0/(1+vд/v0) Т.е. природа эффекта это чисто кинематика! Открыл Доплер, а используют сотрудники ГАИ!

Эффект Доплера наблюдается не только для звуковых волн, но и для электромагнитных (например, световых). Но в этом случае выражение для изменения частоты будет другое, потому что в электромагнитной волне колеблются не частицы среды, как в звуковой волне, а изменяется напряженность поля (электрического и магнитного). Эффект Доплера наблюдается не только для звуковых волн, но и для электромагнитных (например, световых). Но в этом случае выражение для изменения частоты будет другое, потому что в электромагнитной волне колеблются не частицы среды, как в звуковой волне, а изменяется напряженность поля (электрического и магнитного). Если скорость источника звука превышает скорость звука в данной среде, то порождаемые телом возмущения среды остаются позади него и образуют волну, фронт которой имеет форму конической поверхности с вершиной в точке нахождения тела. Именно такую волну, называемую ударной, мы слышим при переходе самолета на сверхзвуковую скорость.

Энергия звуковой волны мала (чайник можно греть 10000 лет) и быстро затухают Энергия звуковой волны мала (чайник можно греть 10000 лет) и быстро затухают Ультразвуковые волны – выше 20 кГц Для локации подводных лодок (П. Ланжевен), айсбергов, косяков рыбы и т.д. Крикнув и измерив время до прихода эха (звука отраженного от скалы и т.п.) можно умножив половину этого времени на скорость звука v=331 м/с (а в водороде 1284, в воде 1490 м/c) найти расстояние до препятствия. Это и используют эхолокаторы и летучие мыши Получают с помощью пьезострикционных или магнитострикционных материалов