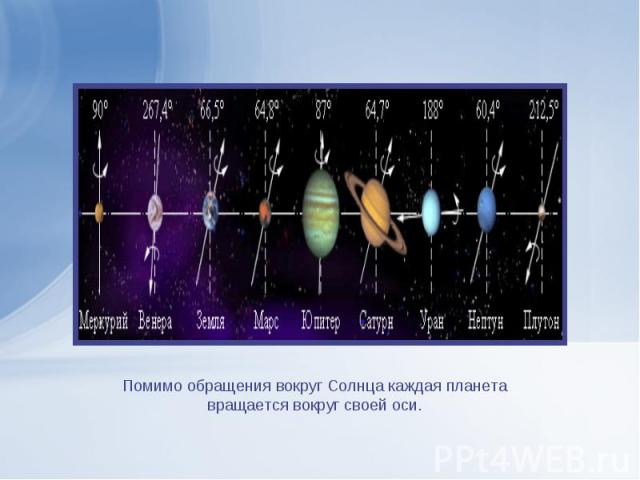
Презентация на тему: Движение в гравитационном поле. Исскуственные спутники Земли

Солнечная система Солнечная система Гравитация внутри Земли Законы Кеплера Движение спутников Элементы орбиты спутника Межпланетный перелет Гравитационный маневр

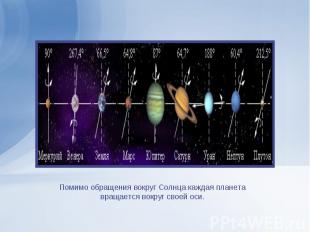
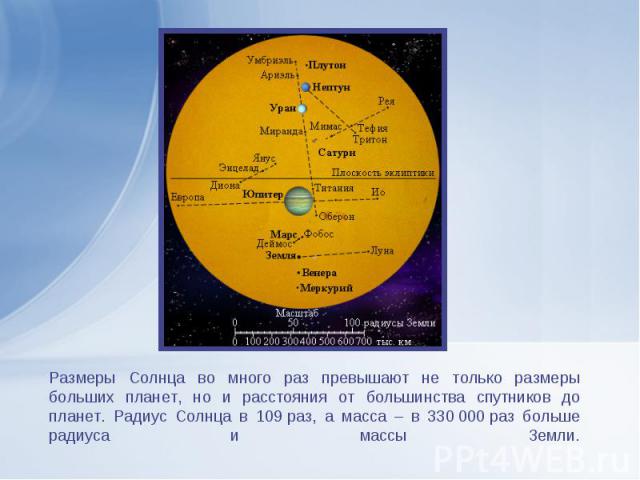
Помимо больших планет в Солнечную систему входят малые планеты (астероиды), составляющие два пояса; один из них находится между орбитами Марса и Юпитера, а второй – пояс Койпера, – за орбитой Нептуна. В настоящее время полагают, что Плутон является одним из объектов пояса Койпера. Далеко за поясом Койпера находится еще одно пылевое облако – облако Оорта. Кроме того, в Солнечную систему входят многочисленные кометы, облетающие Солнце по сильно вытянутым орбитам, межпланетная пыль и газ.

Ускорение, которое испытывает тело m, находящееся на расстоянии r от тела M, равно Ускорение, которое испытывает тело m, находящееся на расстоянии r от тела M, равно

Модель показывает, как изменяется сила тяжести внутри Земли. Из теоремы Гаусса следует, что если считать Землю однородным шаром, сила тяжести внутри ее уменьшается пропорционально расстоянию до центра. Слева изображена Земля (ее правая половина показана в разрезе так, что виден туннель, проходящий на расстоянии L от центра; это расстояние можно менять). В правом нижнем углу изображен график зависимости ускорения свободного падения от расстояния до центра Земли. Серая линия отмечает радиус Земли, равный 6371 км. При нажатии кнопки Старт в туннель начинает падать тело. Силы трения, а также вращение Земли в модели не учитываются. Тело летит к центру туннеля под действием силы тяжести. Модель показывает, как изменяется сила тяжести внутри Земли. Из теоремы Гаусса следует, что если считать Землю однородным шаром, сила тяжести внутри ее уменьшается пропорционально расстоянию до центра. Слева изображена Земля (ее правая половина показана в разрезе так, что виден туннель, проходящий на расстоянии L от центра; это расстояние можно менять). В правом нижнем углу изображен график зависимости ускорения свободного падения от расстояния до центра Земли. Серая линия отмечает радиус Земли, равный 6371 км. При нажатии кнопки Старт в туннель начинает падать тело. Силы трения, а также вращение Земли в модели не учитываются. Тело летит к центру туннеля под действием силы тяжести.

В общем случае невозмущенное движение в гравитационном поле определяется законом сохранения энергии, то есть K + U = сonst, где – кинетическая энергия тела массой m, движущегося со скоростью υ,  – потенциальная энергия этого тела, находящегося на расстоянии r от тела массой M. Константа h называется постоянной энергии. В общем случае невозмущенное движение в гравитационном поле определяется законом сохранения энергии, то есть K + U = сonst, где – кинетическая энергия тела массой m, движущегося со скоростью υ,  – потенциальная энергия этого тела, находящегося на расстоянии r от тела массой M. Константа h называется постоянной энергии.

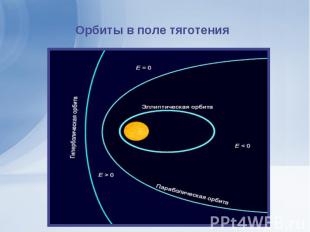
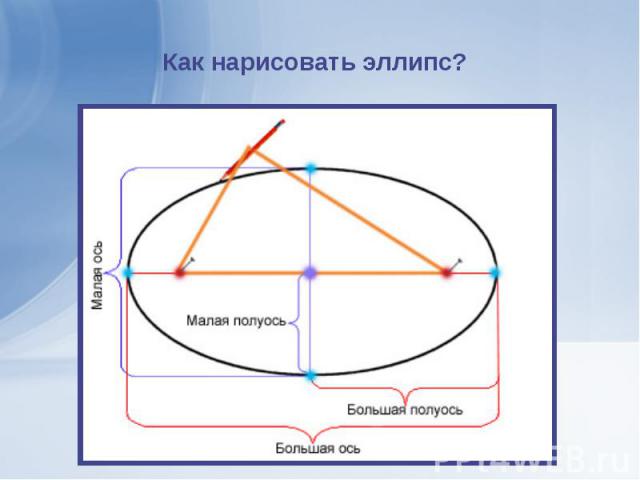
В 1679 году Исаак Ньютон показал, что любое тело в поле тяготения будет двигаться по коническому сечению онические сечения образуются при пересечении прямого кругового конуса с плоскостью. К коническим сечениям относятся кривые второго порядка: эллипс, парабола и гипербола, а также пара параллельных прямых. Все они является геометрическим местом точек, отношение расстояний от которых до заданной точки (фокуса) и до заданной прямой (директрисы) есть величина постоянная, равная эксцентриситету e. При e < 1 получается эллипс, при e = 1 – парабола, при e > 1 – гипербола. В 1679 году Исаак Ньютон показал, что любое тело в поле тяготения будет двигаться по коническому сечению онические сечения образуются при пересечении прямого кругового конуса с плоскостью. К коническим сечениям относятся кривые второго порядка: эллипс, парабола и гипербола, а также пара параллельных прямых. Все они является геометрическим местом точек, отношение расстояний от которых до заданной точки (фокуса) и до заданной прямой (директрисы) есть величина постоянная, равная эксцентриситету e. При e < 1 получается эллипс, при e = 1 – парабола, при e > 1 – гипербола.

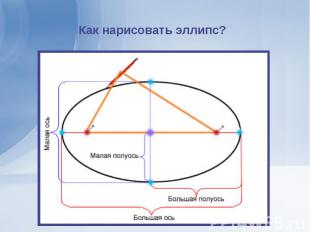
Динамическая модель иллюстрирует законы Кеплера на примере движения спутника Земли. Запуск модели производится кнопкой Старт, приостановка и возвращение в исходное состояние – кнопками Стоп и Сброс соответственно. Группа переключателей Закон позволяет выбрать, какой закон Кеплера будет в настоящий момент иллюстрироваться. Динамическая модель иллюстрирует законы Кеплера на примере движения спутника Земли. Запуск модели производится кнопкой Старт, приостановка и возвращение в исходное состояние – кнопками Стоп и Сброс соответственно. Группа переключателей Закон позволяет выбрать, какой закон Кеплера будет в настоящий момент иллюстрироваться. В центре окна вращается Земля. Вокруг нее по орбите движется спутник. Параметры орбиты (расстояние до Земли в перигее и начальную скорость) можно задать при помощи окон ввода в нижней части модели. В информационном окне приводятся прочие параметры орбиты: длина большой и малой полуосей, эксцентриситет и период обращения, а также виртуальное текущее время. Первый закон Кеплера показывает, что все планеты движутся по эллипсу. Изменением начальной скорости небесного тела вы можете превратить эллиптическую орбиту в гиперболическую: по гиперболическим орбитам мимо Солнца движутся некоторые кометы и ряд спутников, покидающих пределы Солнечной системы.

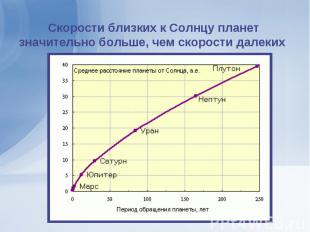
Величина третьей космической скорости зависит от того, в каком направлении корабль выходит из зоны действия земного тяготения Величина третьей космической скорости зависит от того, в каком направлении корабль выходит из зоны действия земного тяготения

Модель демонстрируют основную систему координат, применяемую для описания положения искусственных спутников Земли, – систему орбитальных элементов. Шесть элементов определяют положение и наклон орбиты относительно земного экватора, размеры орбиты и положение спутника на ней. Ось OX направлена на точку весеннего равноденствия. Модель демонстрируют основную систему координат, применяемую для описания положения искусственных спутников Земли, – систему орбитальных элементов. Шесть элементов определяют положение и наклон орбиты относительно земного экватора, размеры орбиты и положение спутника на ней. Ось OX направлена на точку весеннего равноденствия. Если выключатель, соответствующий объекту системы, не выбран, этот объект отображается серым цветом. Если же его выбрать, то объект окрасится ярким цветом, а на схеме появится его название.

Благодаря вращению Земли с космического аппарата за короткое время можно увидеть большую часть поверхности земного шара. Благодаря вращению Земли с космического аппарата за короткое время можно увидеть большую часть поверхности земного шара.

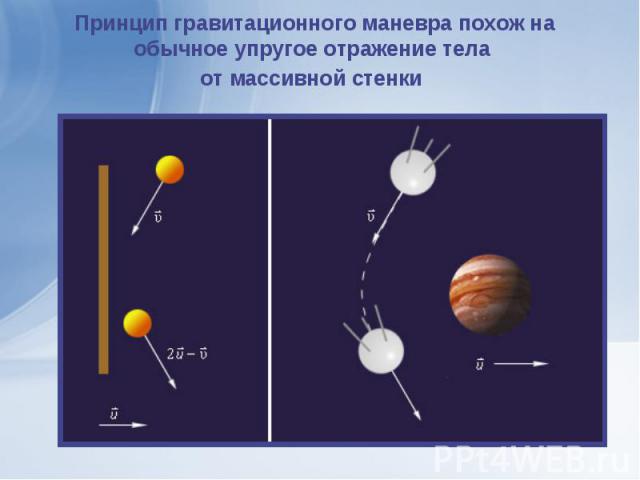
На схемах приведено изменение первоначально круговых орбит импульсами, направленными «по скорости» и «против скорости». Как видно из схем, орбита испытывает наибольшее геометрическое смещение в области, противолежащей точке, в которой телу был сообщен импульс На схемах приведено изменение первоначально круговых орбит импульсами, направленными «по скорости» и «против скорости». Как видно из схем, орбита испытывает наибольшее геометрическое смещение в области, противолежащей точке, в которой телу был сообщен импульс

Модель демонстрирует наиболее выгодную орбиту для межпланетных перелетов. Модель демонстрирует наиболее выгодную орбиту для межпланетных перелетов. Нажмите на кнопку Старт. Ракета, обращающаяся вместе с Землей, включит двигатели и выйдет на промежуточную эллиптическую орбиту (эллипс Гомана). При достижении афелия двигатели включаются еще раз, и космический аппарат перейдет на орбиту Марса. Время старта должно быть точно рассчитано, чтобы в тот момент, когда межпланетная станция перейдет на марсианскую орбиту, планета оказалась в том же месте.

Эффективность маневра изменения плоскости орбиты зависит от того, в какой точке орбиты он выполняется Эффективность маневра изменения плоскости орбиты зависит от того, в какой точке орбиты он выполняется

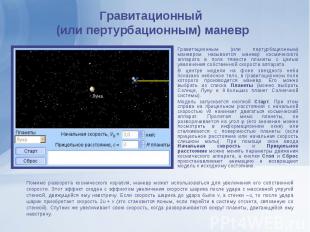
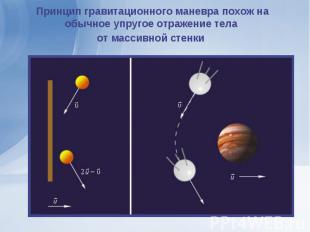
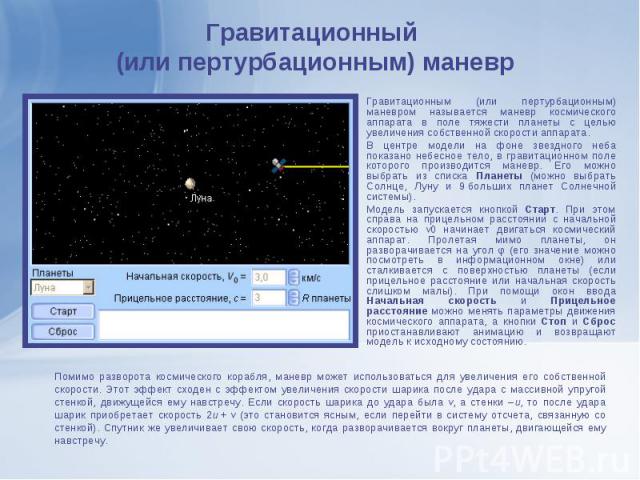
Гравитационным (или пертурбационным) маневром называется маневр космического аппарата в поле тяжести планеты с целью увеличения собственной скорости аппарата. Гравитационным (или пертурбационным) маневром называется маневр космического аппарата в поле тяжести планеты с целью увеличения собственной скорости аппарата. В центре модели на фоне звездного неба показано небесное тело, в гравитационном поле которого производится маневр. Его можно выбрать из списка Планеты (можно выбрать Солнце, Луну и 9 больших планет Солнечной системы). Модель запускается кнопкой Старт. При этом справа на прицельном расстоянии с начальной скоростью v0 начинает двигаться космический аппарат. Пролетая мимо планеты, он разворачивается на угол φ (его значение можно посмотреть в информационном окне) или сталкивается с поверхностью планеты (если прицельное расстояние или начальная скорость слишком малы). При помощи окон ввода Начальная скорость и Прицельное расстояние можно менять параметры движения космического аппарата, а кнопки Стоп и Сброс приостанавливают анимацию и возвращают модель к исходному состоянию.