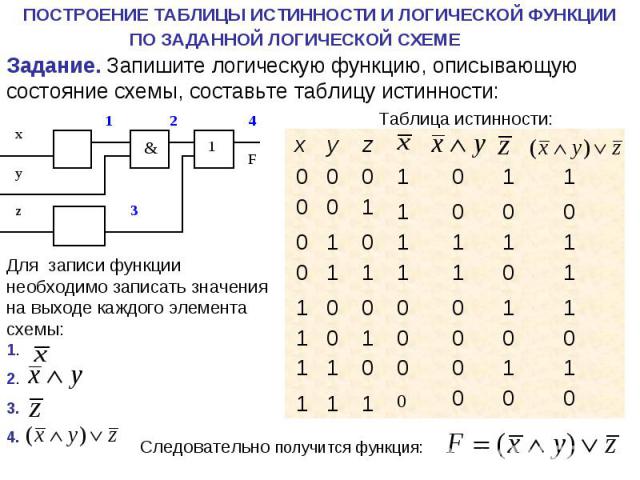
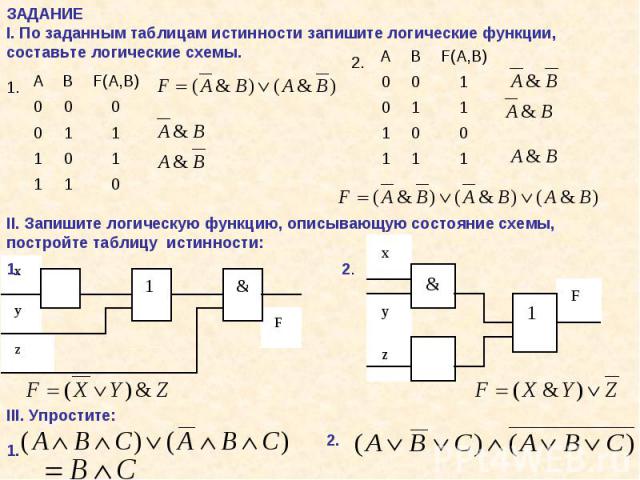
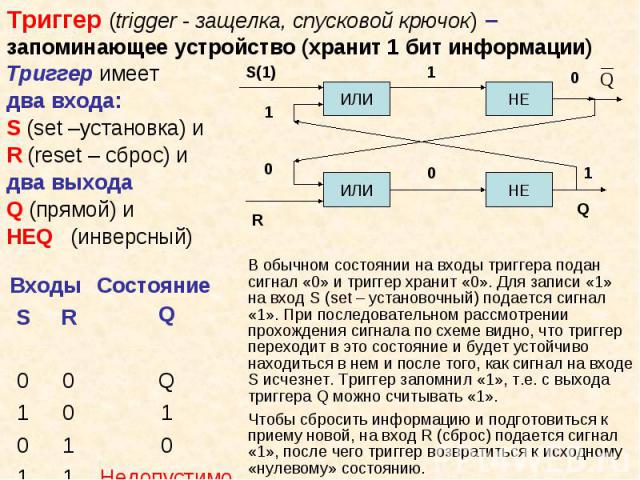
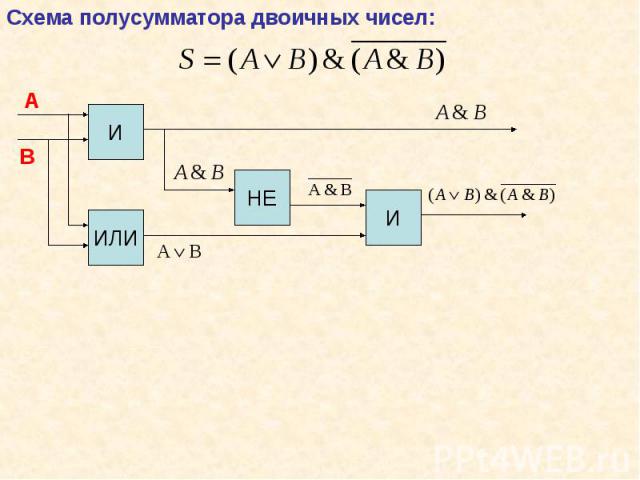
Презентация на тему: Логические функции

Понятие – форма мышления, фиксирующая основные существенные признаки объекта. Понятие – форма мышления, фиксирующая основные существенные признаки объекта. Понятие имеет: Содержание – совокупность существенных признаков объекта. Объем – совокупность предметов, на которые оно распространяется. Пример: Содержание понятия «Персональный компьютер» - «Персональный компьютер – это универсальное электронное устройство для автоматической обработки информации, предназначенное для одного пользователя» Объем понятия «Персональный компьютер» выражает всю совокупность существующих сейчас в мире персональных компьютеров.

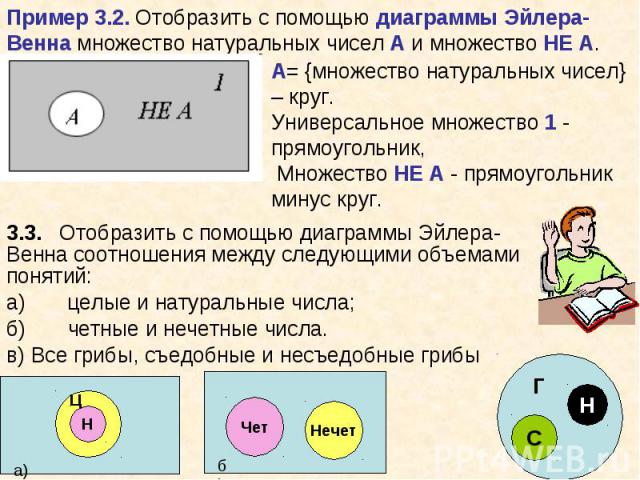
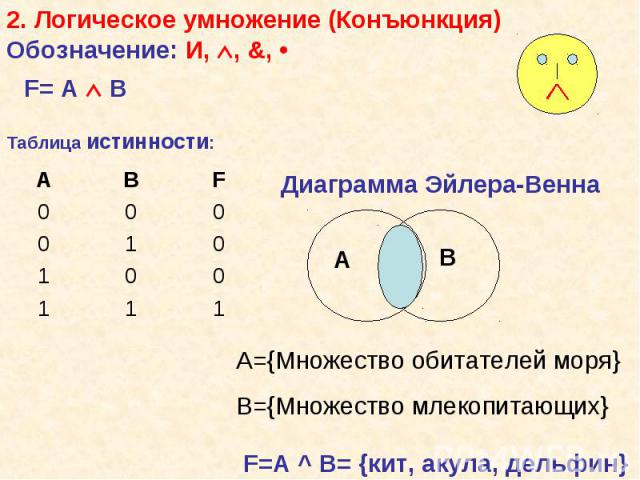
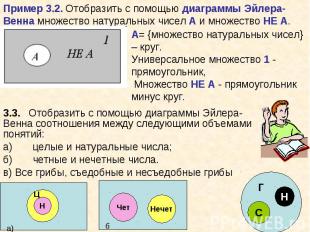
Объем понятия может быть представлено в форме множества объектов, состоящего из элементов множества. Алгебра множеств, одна из основополагающих современных математических теорий, позволяет исследовать отношения между множествами и, соответственно, объемами понятий. Объем понятия может быть представлено в форме множества объектов, состоящего из элементов множества. Алгебра множеств, одна из основополагающих современных математических теорий, позволяет исследовать отношения между множествами и, соответственно, объемами понятий. Между множествами (объемами понятий) могут быть различные виды отношений: равнозначность, когда объемы понятий полностью совпадают; пересечение, когда объемы понятий частично совпадают; подчинения, когда объем одного понятия полностью входит в объем другого и т.д. Для наглядной геометрической иллюстрации объемов понятий и соотношений между ними используются диаграммы Эйлера-Венна. Если имеются какие-либо понятия A, B, C и т.д., то объем каждого понятия (множество) можно представить в виде круга, а отношения между этими объемами (множествами) в виде пересекающихся кругов.

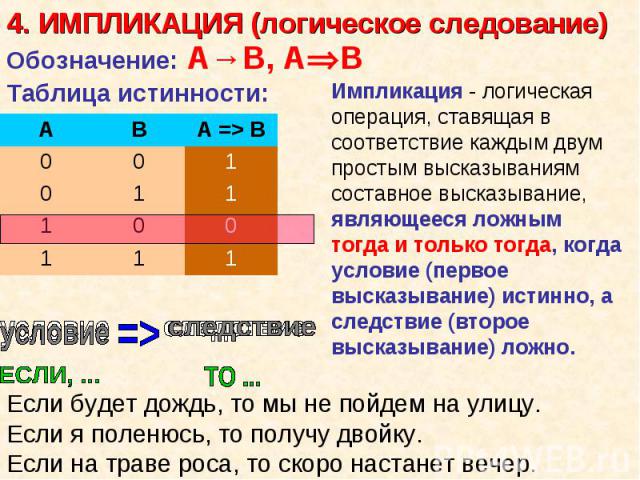
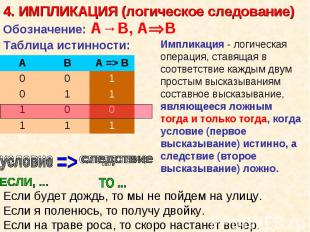
Пример: Пример: «Все углы треугольника равны» (посылка), то «Этот треугольник равносторонний» (заключение) Посылками умозаключений по правилам формальной логики могут быть только истинные суждения, и тогда умозаключение будет истинным. В противном случае можно прийти к ложному умозаключению.

Какие существуют основные формы мышления? Какие существуют основные формы мышления? В чем состоит разница между содержанием и объемом понятия? Может ли быть высказывание выражено в форме вопросительного предложения? Как вычисляется истинность или ложность простого высказывания? Составного высказывания?

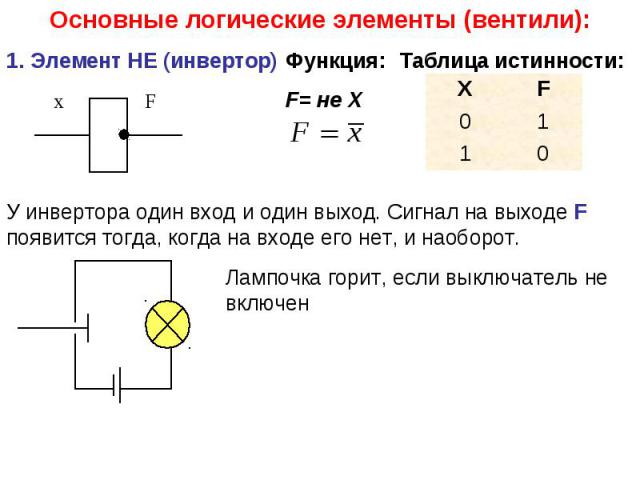
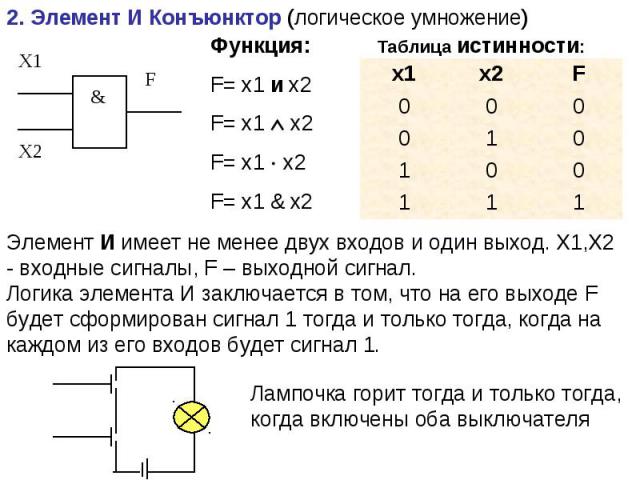
Англичанин Джордж Буль (1815-1864, математик-самоучка), на фундаменте, заложенном Лейбницем, создал новую область науки - Математическую логику (Булеву алгебру или Алгебру высказываний). В его работах логика обрела свой алфавит, свою орфографию и грамматику.

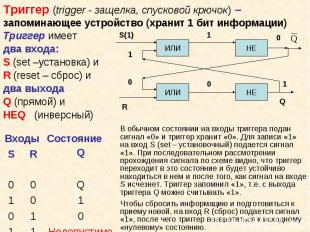
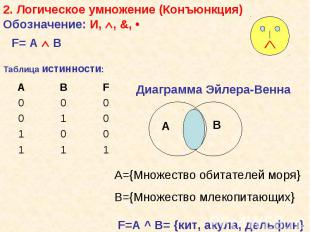
Различают: Различают: Логические константы (логические утверждения) – конкретные частные утверждения (И/Л) {Аристотель - основоположник логики} {На яблонях растут бананы} 2. Логические переменные (предикаты) – логические высказывания, значения которых меняются в зависимости от входящих в них переменных, обозначаются заглавными латинскими буквами А, В, С, D, F,… А = {Аристотель - основоположник логики} В = {На яблонях растут бананы}. Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом, А = 1, В = 0.

Определите, в каком порядке необходимо вычислять значение логического выражения: Определите, в каком порядке необходимо вычислять значение логического выражения: 1) ¬ А & ¬ B 2) A & (B & C) 3) (A & B) ν (C & ¬ D) 4) A ν ¬ D ν B 5) A → (B ↔ ¬ A)

Пример1. Пример1. Вычислить значение логического выражения «(2·2=5 или 2·2=4}) и (2·2 ≠ 5 или 2·2 ≠ 4)»

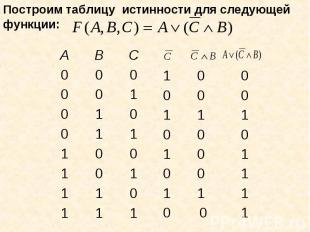
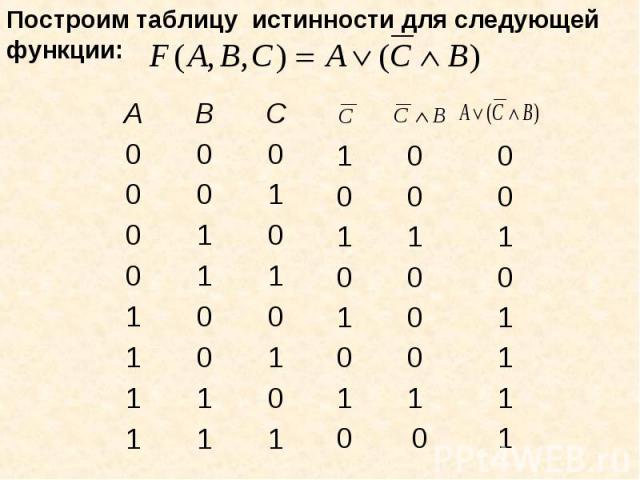
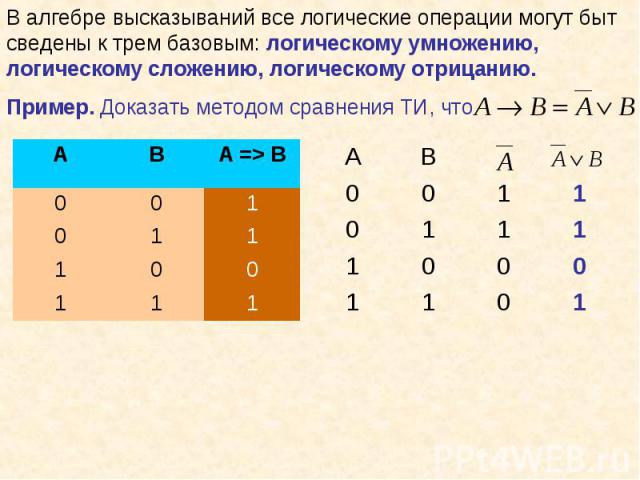
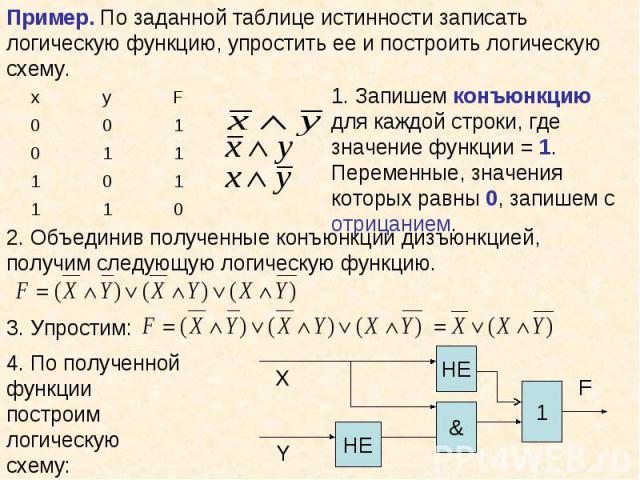
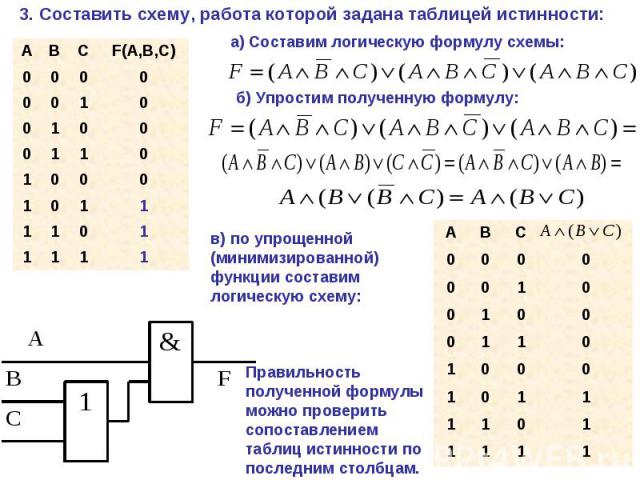
Логические выражения, у которых последние столбцы в таблице истинности совпадают, называются равносильными. Логические выражения, у которых последние столбцы в таблице истинности совпадают, называются равносильными. Знак «=» - равносильность.

№ 3.2. (Д.р.) Записать составное выражение № 3.2. (Д.р.) Записать составное выражение «(2·2=4 и 3·3=9) или (2·2≠4 и 3·3≠9)» в форме логического выражения . Построить ТИ.

3. Какое существует количество логических функций трех аргументов? 3. Какое существует количество логических функций трех аргументов?

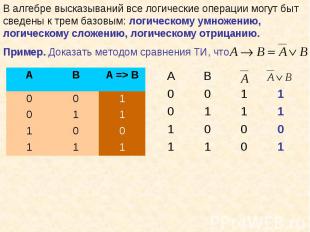
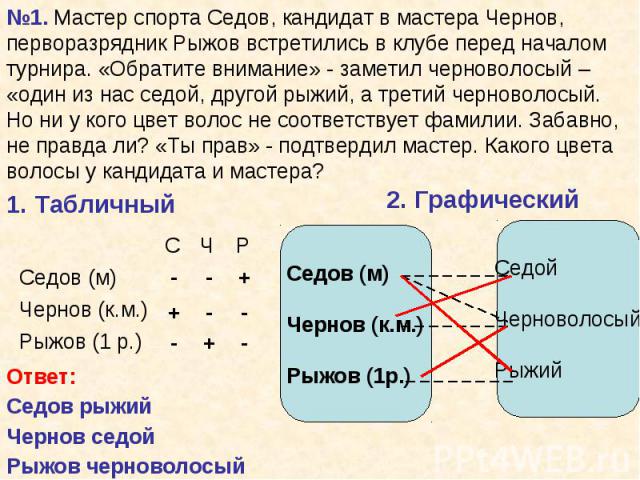
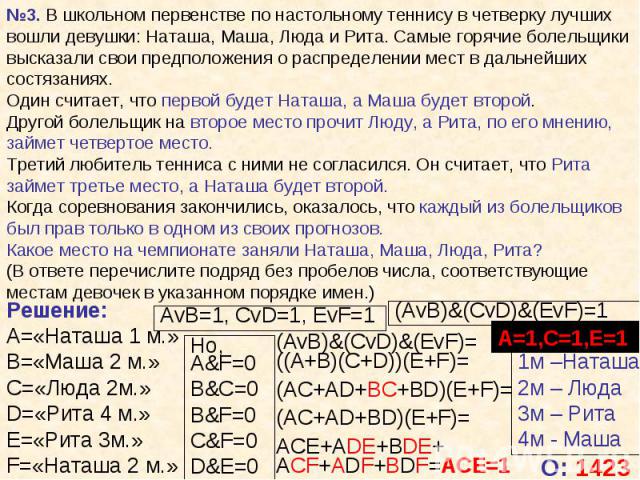
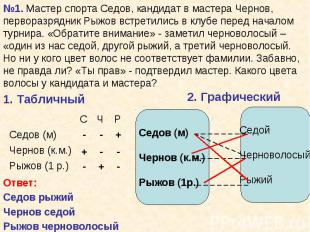
Способы решения: Способы решения: Табличный Графический (Графы) Средствами алгебры логики

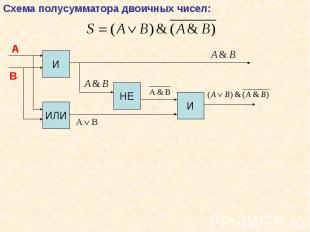
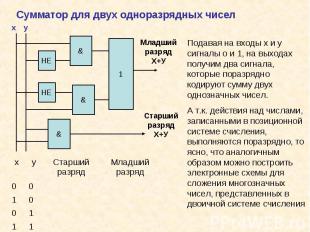
Двоичная система оказалась удобной в качестве языка логики. Это поняли спустя 100 лет после работ Буля. Двоичная система оказалась удобной в качестве языка логики. Это поняли спустя 100 лет после работ Буля.