Презентация на тему: Высказывания

ВЫСКАЗЫВАНИЯ Тема 3

Тема 2 1. Высказывание и суждение. Структура и виды высказываний 2. Простые атрибутивные высказывания и отношения между ними. Логический квадрат 3. Операции с простыми высказываниями 4. Сложные высказывания. Логические союзы 5. Табличный способ установления истинности сложных высказываний

Тема 3 1. Высказывание и суждение. Структура и виды высказываний Высказывание – языковое выражение, которое можно оценить как истинное или ложное. Форма мышления, соответствующая высказыванию – суждение. Суждение – «высказывание, утверждающее или отрицающее, что-нибудь о чем-нибудь» (Аристотель) Суждение – связь двух и более понятий, устанавливающая отношение между предметами и их признаками. Например: «Аристотель – ученик Платона», «Платон мне друг», «Всякая вещь имеет четыре причины», «Холодает», «Иван старше Петра», «Он существует» и т.п. Вопросительные и перформативные предложения (т.е. выражающие обращение, призыв, приказ и т.п.) высказываниями не являются. Например: «Который час?», «Добро пожаловать!», «Посторонним вход воспрещен!» …

Структура высказывания Высказывание состоит из субъекта, предиката и логической связки. Субъект и предикат называются терминами высказывания. Субъект (subjectum – «подлежащее») – имя, указывающее на предмет мысли; предмет, о котором нечто утверждается (отрицается). Предикат (praedicatum – «сказанное») – имя, указывающее на свойство предмета мысли; то, что утверждается (отрицается) о предмете мысли (субъекте). Логическая связка (обычно, слово «есть») указывает на отношение между предметом мысли и его свойством (например, на принадлежность свойства или его отсутствие) СУБЪЕКТ связка ПРЕДИКАТ Например: «Диоген устроил себе жилье в глиняной бочке»

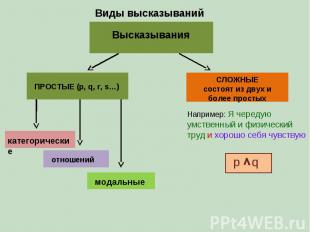
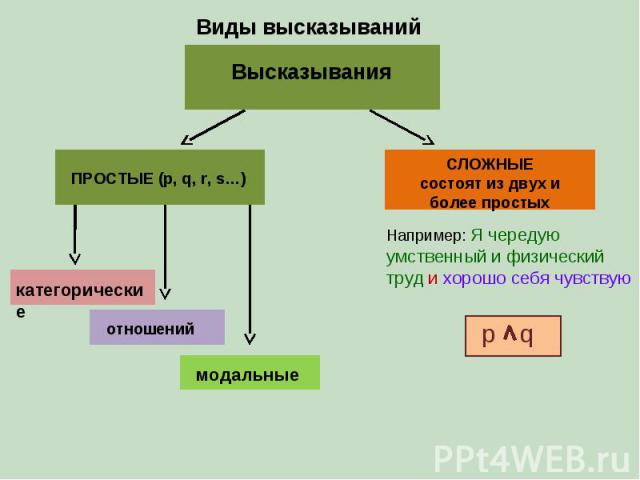
Виды высказываний Высказывания ПРОСТЫЕ (p, q, r, s…) СЛОЖНЫЕ состоят из двух и более простых категорические отношений модальные Например: Я чередую умственный и физический труд и хорошо себя чувствую p q

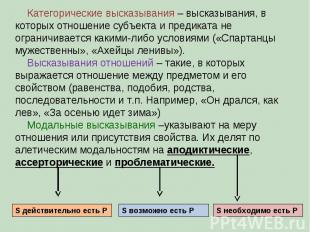
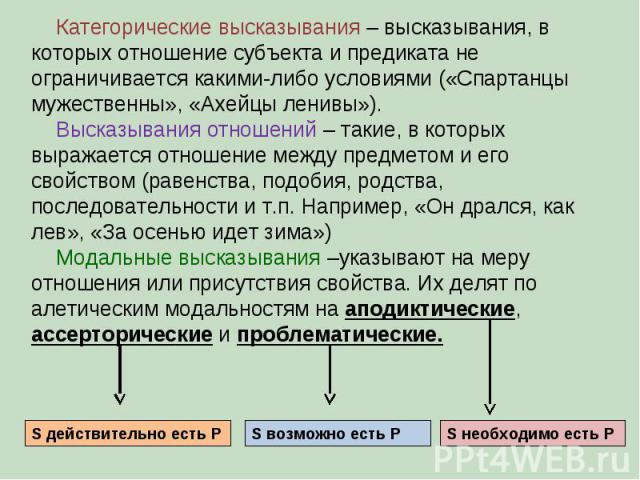
Категорические высказывания – высказывания, в которых отношение субъекта и предиката не ограничивается какими-либо условиями («Спартанцы мужественны», «Ахейцы ленивы»). Высказывания отношений – такие, в которых выражается отношение между предметом и его свойством (равенства, подобия, родства, последовательности и т.п. Например, «Он дрался, как лев», «За осенью идет зима») Модальные высказывания –указывают на меру отношения или присутствия свойства. Их делят по алетическим модальностям на аподиктические, ассерторические и проблематические. S необходимо есть P S возможно есть P S действительно есть P

Простые атрибутивные высказывания – такие, в которых предмету приписывается некоторое свойство («Осенью прохладно», «Всякий моряк ходил за горизонт»…) Они бывают по качеству связки: положительные (S есть P) отрицательные (S не есть P); по количественному параметру субъекта: единичные (Данный S есть P) частные (Некоторые S есть P) общие (Все S есть P).

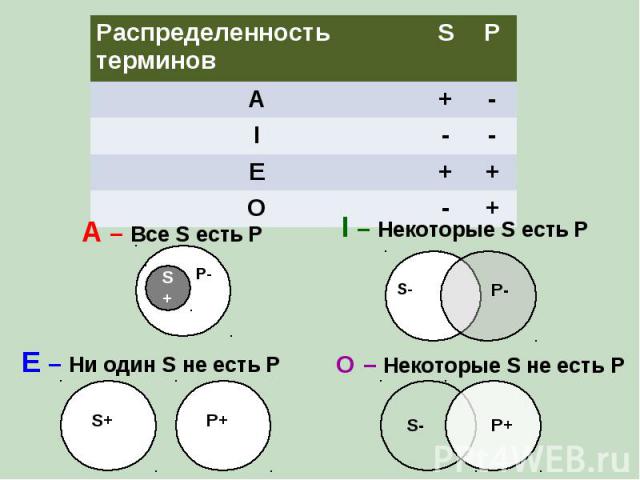
AFFIRMO NEGO A – общеутвердительное Все S есть P I – частноутвердительное Некоторые S есть P E – общеотрицательное Ни один S не есть P O – частноотрицательное Некоторые S не есть P Михаил Псёлл, XI в.

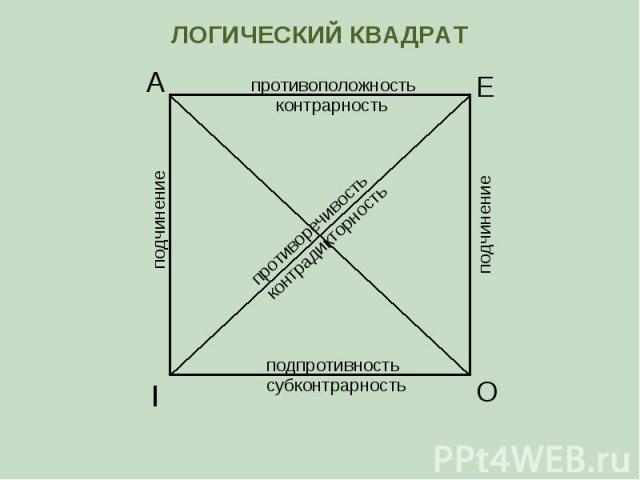
А Е I O противоположность контрарность субконтрарность подпротивность противоречивость контрадикторность подчинение подчинение ЛОГИЧЕСКИЙ КВАДРАТ

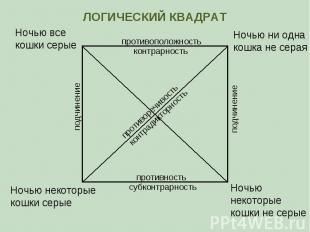
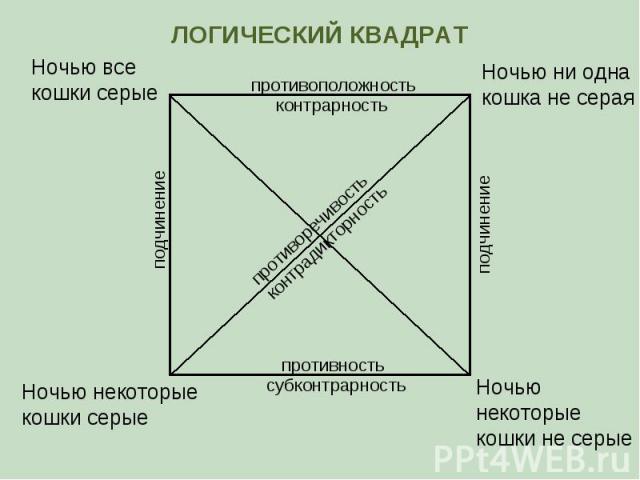
Ночью все кошки серые Ночью ни одна кошка не серая Ночью некоторые кошки серые Ночью некоторые кошки не серые противоположность контрарность субконтрарность противность противоречивость контрадикторность подчинение подчинение ЛОГИЧЕСКИЙ КВАДРАТ

Противоположные (контрарные) высказывания А и Е могут быть одновременно ложными, но не могут быть одновременно истинными Подпротивные (субконтрарные) высказывания I и O могут быть одновременно истинными, но не могут быть одновременно ложными Противоречивые (контрадикторные) высказывания (А и O или Е и I) не могут быть одновременно ни истинными, ни ложными (одно из них всегда истинно, а другое ложно) Если подчиняющее высказывание А или Е истинно, то подчиненное I или O также истинно. Если же подчиненное высказывание I или O ложно, то подчиняющее А или Е также ложно

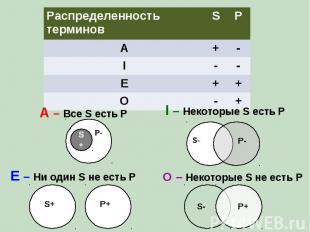
Распределенность терминов S P A + - I - - E + + O - + A – Все S есть P I – Некоторые S есть P E – Ни один S не есть P O – Некоторые S не есть P P S+ Р- P- S+ P+ S- P+ S-

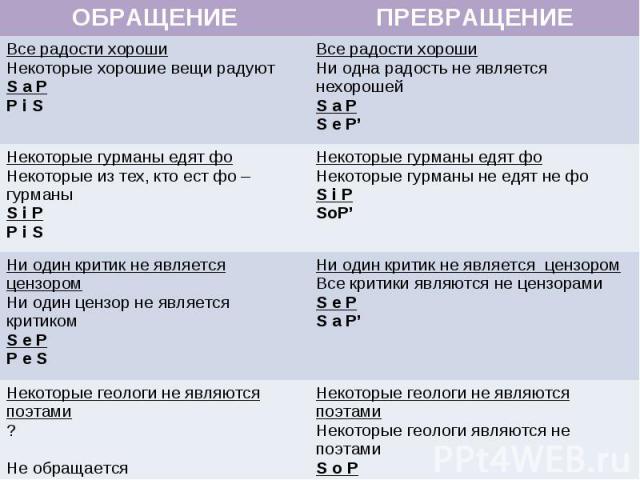
3. Операции с простыми высказываниями Обращение (конверсия) – это логическая операция, при которой термины высказывания меняются местами (субъект становится предикатом, и наоборот) Все полные люди добродушны Некоторые добряки – полные Превращение (обверсия) – логическая операция, при которой меняется качество высказывания (утвердительное становится отрицательным, и наоборот) Ни один моряк не является рыбаком Все моряки являются нерыбаками Противопоставление (контрапозиция) – операция, при которой производится обращение, а затем превращение, или наоборот (противопоставление субъекту и противопоставление предикату) Все японцы занимаются сумо Некоторые сумоисты – японцы Некоторые сумоисты не являются не японцами P S+ Р- S+ P+ Ни один буддист не является даосом Все буддисты – не даосы Некоторые не даосы – буддисты

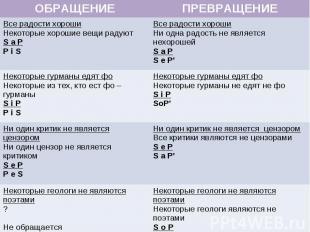
ОБРАЩЕНИЕ ПРЕВРАЩЕНИЕ Все радости хороши Некоторые хорошие вещи радуют S a P P i S Все радости хороши Ни одна радость не является нехорошей S a P S e P’ Некоторые гурманы едят фо Некоторые из тех, кто ест фо – гурманы S i P P i S Некоторые гурманы едят фо Некоторые гурманы не едят не фо S i P SoP’ Ни один критик не является цензором Ни один цензор не является критиком S e P P e S Ни один критик не является цензором Все критики являются не цензорами S e P S a P’ Некоторые геологи не являются поэтами ? Не обращается Некоторые геологи не являются поэтами Некоторые геологи являются не поэтами S o P S i P’

Выявим логическую форму приведенного выражения (формализуем его): Найдем простые высказывания и союзы Простые высказывания обозначим буквами (p, q, r, s), логические союзы – символами. Установим способы связи между простыми высказываниями и их последовательность Запишем выражение в символическом виде pᴧq ᴧ(r→s) 4. Сложные высказывания. Логические союзы Сложное высказывание – выражение, состоящее из простых высказываний (переменных), связанных логическими союзами (функторами) Логический союз – выражение, определяющее характер связи простых высказываний в составе сложного Иван Иванович чрезвычайно тонкий человек и в порядочном разговоре никогда не скажет неприличного слова и тотчас обидится, если услышит его. (Н. В. Гоголь)

Логические союзы Обозначение Название Языковое выражение «‾»; «¬» ¬p; p отрицание «не», «неверно, что» Λ конъюнкция «и», «а», «но», «да», «вместе с тем» и др. V дизъюнкция «или» сильная дизъюнкция «либо» → импликация «если…, то» ↔ эквиваленция «тогда и только тогда, когда» Логический союз определяет вид сложного высказывания: конъюнктивное (соединительное), дизъюнктивное (разъединительное), импликативное (условное), эквивалентное (взаимообусловленное)

5. Табличный способ установления истинности сложных высказываний Истинность сложного высказывания зависит от истинности простых, входящих в его состав, а также логических союзов Условия истинности сложных высказываний задаются логической двузначностью и таблицами истинности для логических союзов Таблица истинности позволяет установить условия истинности сложных высказываний различного вида при различных логических значениях переменных Количество строк в таблице определяется количеством переменных, каждая из которых может принимать два значения (“истина” и “ложь”), т.е. равно количеству переменных возведенному во вторую степень. p ¬p И Л Л И Отрицание истинно, когда исходное высказывание ложно и наоборот

p q p ᴧ q И И И И Л Л Л И Л Л Л Л p q p V q И И И И Л И Л И И Л Л Л p q p q И И Л И Л И Л И И Л Л Л Конъюнкция Дизъюнкция Сильная дизъюнкция

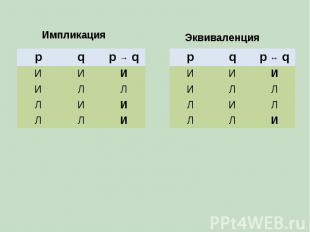
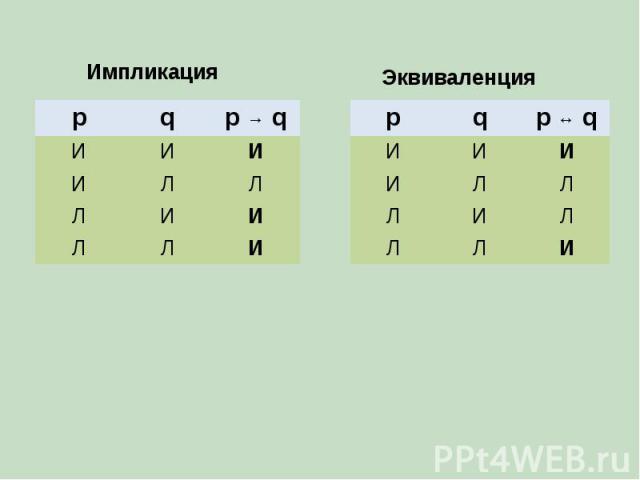
Импликация p q p → q И И И И Л Л Л И И Л Л И p q p ↔ q И И И И Л Л Л И Л Л Л И Эквиваленция

Установим значения переменных, при которых истинно следующее высказывание: ((p →q) p) → q p q p→q (p→q) p ((p →q) p) → q И И И И И И Л Л Л И Л И И Л И Л Л И Л И Высказывание истинно при любых значениях переменных. Подобные выражения являются логическими законами.

Логические законы – правильные схемы рассуждений – логические схемы, которые при любых подстановках преобразуются только в истинные выражения. Если цветы не поливать, они завянут Цветы не поливали Они завяли Выполнимые схемы рассуждений – логические схемы, которые при одних подстановках преобразуются в истинные, а при других в ложные выражения. Если цветы не поливать, они завянут Цветы поливали Они не завяли Противоречивые (невыполнимые) схемы рассуждения – логические схемы, которые при любых подстановках преобразуются исключительно в ложные выражения. Неправда, что цветы всегда либо вянут, либо не вянут