Презентация на тему: Понятие о производной функции

Понятие о производной функции, её геометрический и физический смысл. Уравнение касательной к графику функции

Цели урока: ОБУЧАЮЩАЯ : 1) Ввести определение производной функции на основе задач физики, рассматривая при этом физический смысл производной; 2) Выяснить геометрический смысл производной дифференцируемой функции; 3) Вывести уравнение касательной к графику функции, с использованием производной; 4) Научиться решать задачи на данную тему, используя полученные знания РАЗВИВАЮЩАЯ : 1) Способствовать развитию общения как метода научного познания, аналитико-синтетического мышления, смысловой памяти и произвольного внимания, 2) Развитие навыков исследовательской деятельности ВОСПИТАТЕЛЬНАЯ : 1) Способствовать развитию творческой деятельности 2) Развивать у учащихся коммуникативные компетенции, потребности к самообразованию.

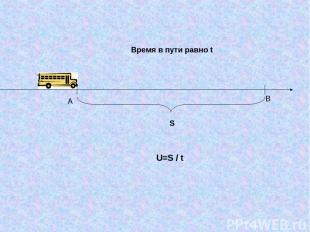
S Время в пути равно t А B U=S / t

ЗАДАЧА. По прямой, на которой заданы начало отсчета, единица измерения(метр) и наравление, движется некоторое тело (материальная точка). Закон движения задан формулой S=s(t), где t – время (в секундах), s(t) – положение тела на прямой (координата движущейся материальной точки) в момент времени t по отношению к началу отсчета (в метрах). Найти скорость движения тела в момент времени t (в м/с). РЕШЕНИЕ. Предположим, что в момент времени t тело находилось в точке M ∆ s M P O OM=S(t). Дадим аргументу t приращение ∆t и рассмотрим ситуацию в момент времени t + ∆t . Координата материальной точки станет другой, тело в этот момент будет находиться в точке P: OP= s(t+ ∆t) – s(t). Значит, за ∆t секунд тело переместилось из точки M в точку P. Имеем: MP=OP – OM = s(t+ ∆t) – s(t). Полученная разность называется приращением функции: s(t+ ∆t) – s(t)= ∆s. Итак, MP= ∆s (м). Тогда средняя скорость на промежутке времени [t; t+∆t]: ʋ ср= ∆s/ ∆t (м/c)

А что такое ʋ(t) в момент времени t, (её называют мгновенной скоростью). Т.е. мгновенная скорость – это средняя скорость на промежутке [t; t+∆t] при условии, что ∆t→0. Это значит, что : ʋ(t)=lim ∆s / ∆t ∆t→0

Предел приращения функции к приращению аргумента, если он существует, называют производной функции в точке x0 и пишут:

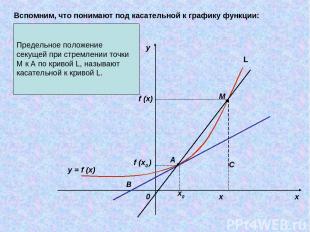
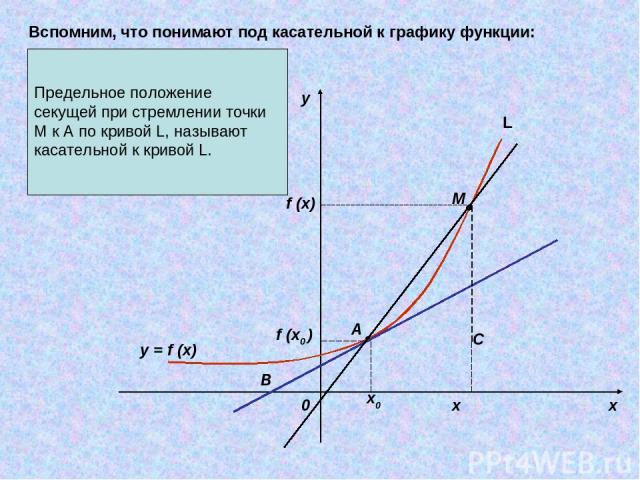
Предельное положение секущей при стремлении точки M к A по кривой L, называют касательной к кривой L. y x 0 x0 x f (x0 ) f (x) M A B C y = f (x) Вспомним, что понимают под касательной к графику функции: L

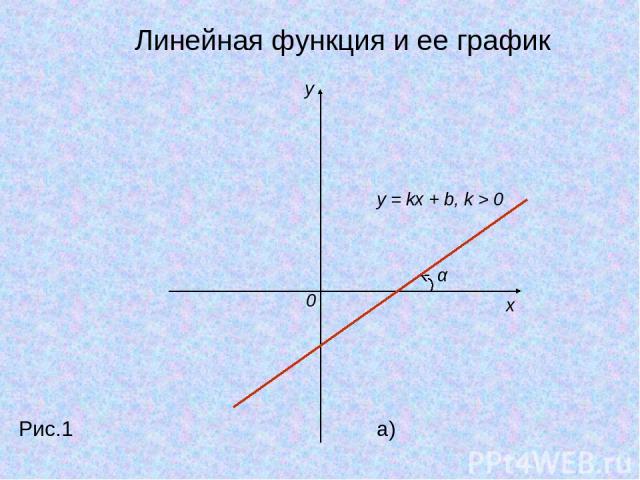
Линейная функция и ее график Какой вид имеет линейная функция? y = kx+b - линейная функция. Что является графиком линейной функции? Графиком линейной функции является прямая. Число k называется угловым коэффициентом прямой. Угол α – углом между этой прямой и положительным направлением оси Ox.

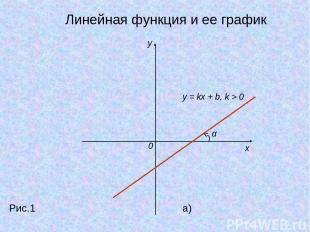
y x 0 y = kx + b, k > 0 α Рис.1 a) Линейная функция и ее график

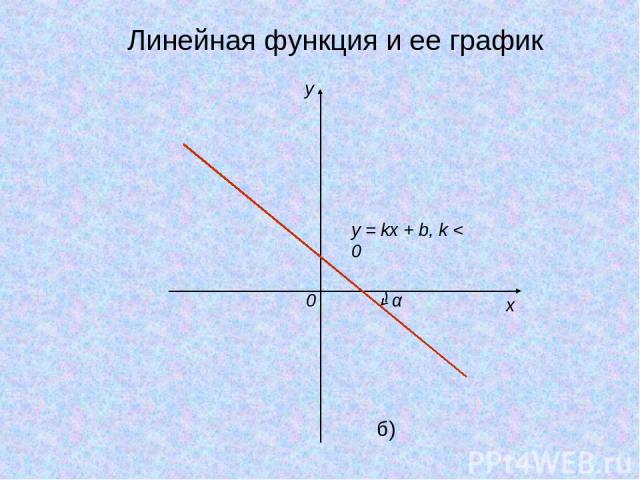
y x 0 y = kx + b, k < 0 α б) Линейная функция и ее график

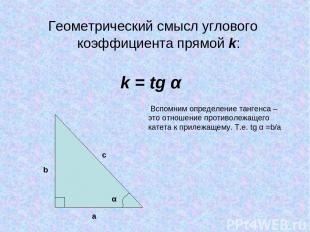
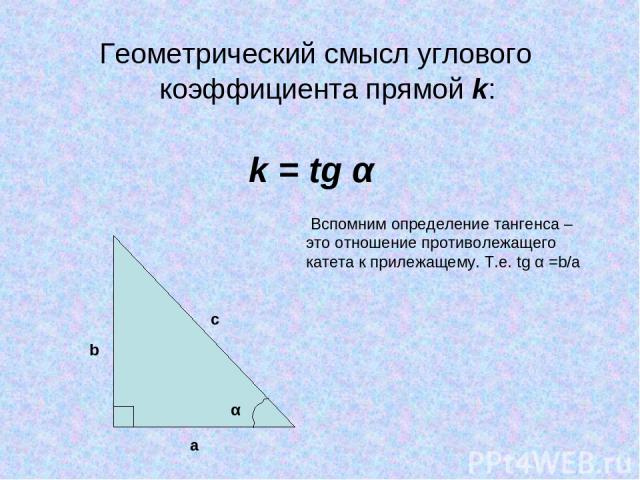
Геометрический смысл углового коэффициента прямой k: k = tg α a b c Вспомним определение тангенса – это отношение противолежащего катета к прилежащему. Т.е. tg α =b/a α

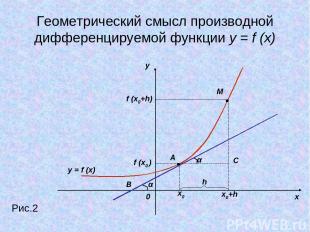
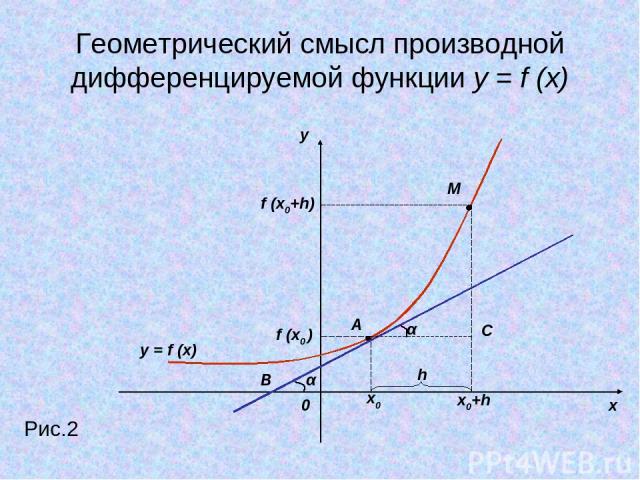
Геометрический смысл производной дифференцируемой функции y = f (x) y x 0 Рис.2 y = f (x) x0 x0+h f (x0 ) f (x0+h) M A h α α B С

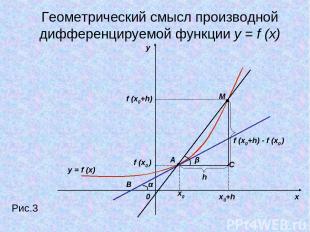
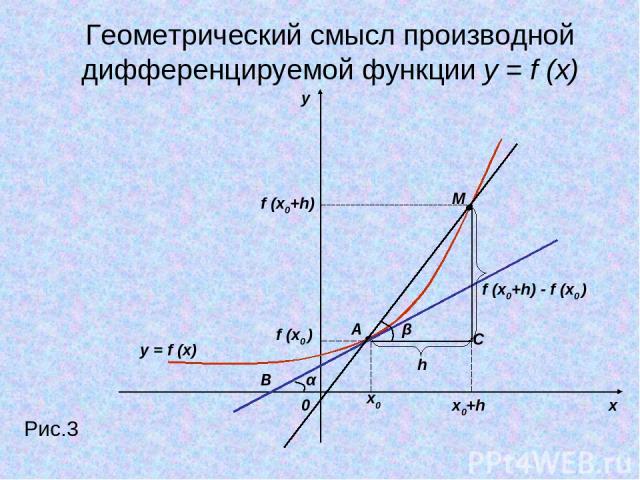
y x 0 Рис.3 x0 x0+h f (x0 ) f (x0+h) M A h α B β f (x0+h) - f (x0 ) C Геометрический смысл производной дифференцируемой функции y = f (x) y = f (x)

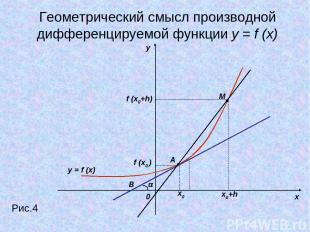
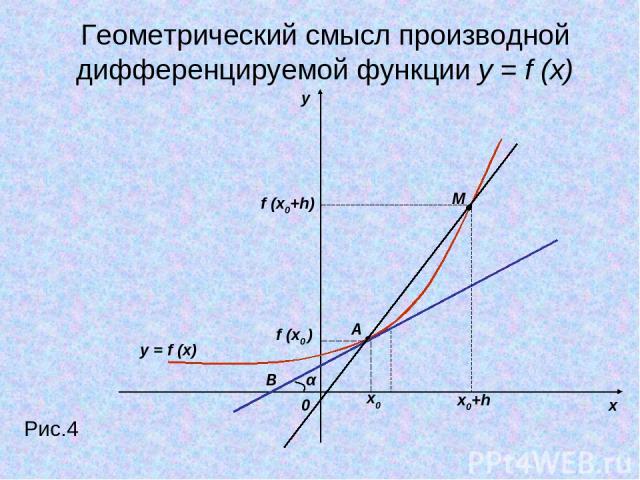
y x 0 Рис.4 y = f (x) x0 x0+h f (x0 ) f (x0+h) M A α B Геометрический смысл производной дифференцируемой функции y = f (x)

Геометрический смысл производной дифференцируемой функции y = f (x): Значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке.

Алгоритм нахождения производной функции

Уравнение касательной к графику функции

Домашнее задание Решить предложенные в карточках примеры, для домашнего изучения