Презентация на тему: Показательная функция

«Показательная функция»Учитель математики МАОУ лицей №3 города Кропоткин Краснодарского края Зозуля Елена Алексеевна

Цель:Рассмотрение основных свойств показательной функции.Построение графика.Решение показательных уравнений.Решение показательных неравенств.

ОпределениеПоказательная функция – это функция вида , где x – переменная, - заданное число, >0, 1.Примеры

Свойства показательной функции Область определения: все действительные числа Множество значений: все положительные числаПри > 1 функция возрастающая;при 0 < < 1 функция убывающая.

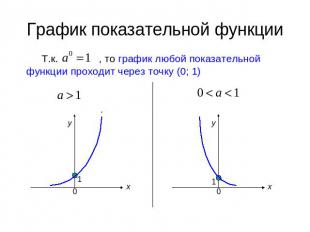
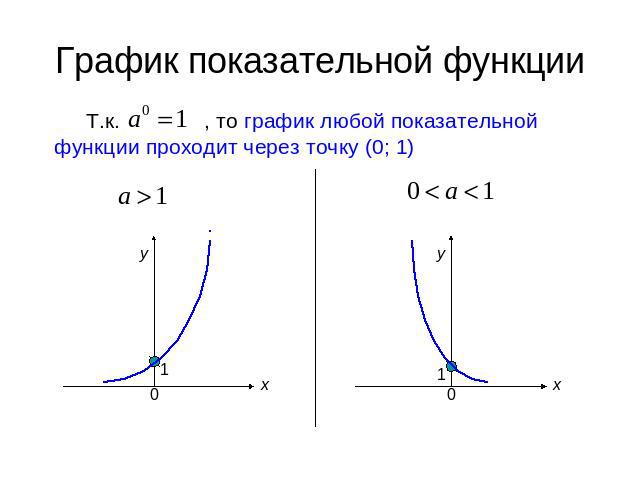
График показательной функцииТ.к. , то график любой показательной функции проходит через точку (0; 1)

Показательные уравненияОпределениеПростейшие уравненияСпособы решения сложных уравнений

Определение Уравнение, в котором переменная содержится в показателе степени, называется показательным.

Простейшее показательное уравнение – это уравнение вида Простейшее показательное уравнение решается с использованием свойств степени.

Способы решения сложных показательных уравнений.Замена переменнойДеление на показательную функциюВынесение за скобки степени с меньшим показателем

Вынесение за скобки степени с меньшим показателемДанный способ используется, если соблюдаются два условия: 1) основания степеней одинаковы;2) коэффициенты перед переменной одинаковы

Замена переменнойПри данном способе показательное уравнение сводится к квадратному.Способ замены переменной используют, еслиа) основания степеней одинаковы;б)показатель одной из степеней в 2 раза больше, чем коэффициенты передпеременной противоположны.

Деление на показательную функциюДанный способ используется, если основания степеней разные.а) в уравнении вида ax = bx делим на bx Например: 2х = 5х | : 5xб) в уравнении A a2x + B (ab)x + C b2x = 0 делим на b2x. Например: 325х - 815х + 59х = 0 | : 9x

Показательные неравенстваОпределениеПростейшие неравенстваРешение неравенств

ОпределениеПоказательные неравенства – это неравенства, в которых неизвестное содержится в показателе степени.

Простейшие показательные неравенства – это неравенства вида:

При решении простейших неравенств используют свойства возрастания или убывания показательной функции.Для решения более сложных показательных неравенств используются те же способы, что и при решении показательных уравнений.

Показательная функцияПостроение графикаСравнение чисел с использованием свойств показательной функцииСравнение числа с 1 а) аналитический способ; б) графический способ.

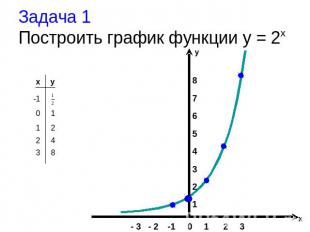
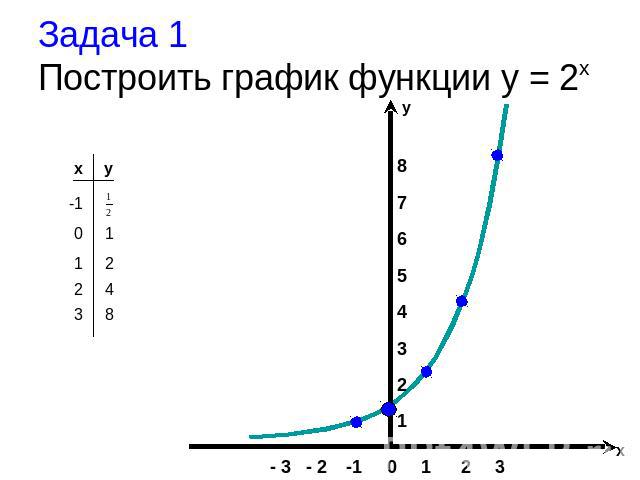
Задача 1 Построить график функции y = 2x

Задача 2Сравнить числа

Задача 3Сравнить число с 1. Решение

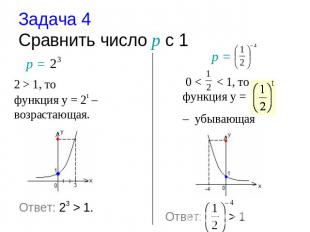
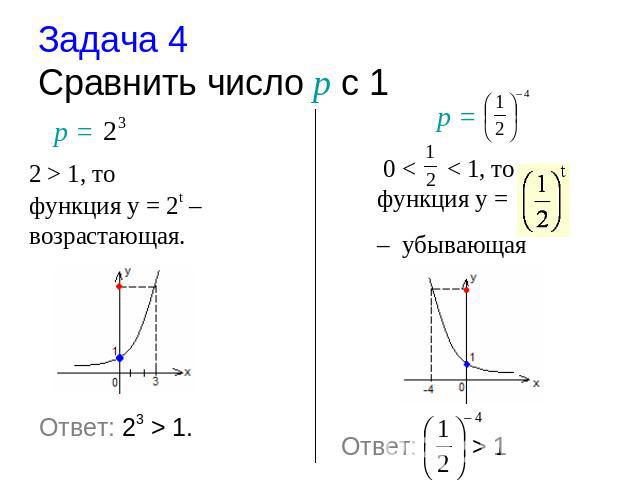
Задача 4 Cравнить число р с 1 2 > 1, то функция у = 2t – возрастающая. 0 < < 1, то функция у = – убывающая

Решение показательных уравненийПростейшие показательные уравненияУравнения, решаемые вынесением за скобки степени с меньшим показателемУравнения, решаемые заменой переменной случай 1; случай 2.Уравнения, решаемые делением на показательную функцию случай 1; случай 2.

Простейшие показательные уравнения

Вынесение за скобки степени с меньшим показателем

Замена переменной (1)основания степеней одинаковы, показатель одной из степеней в 2 раза больше, чем у другой .3 2x – 4 · 3 х – 45 = 0 По т. Виета: t1· t 2 = - 45; t1+ t 2 =4t1 = 9; t 2 = - 5 – не удовлетворяет условию

Замена переменной (2)Основания степеней одинаковы, коэффициенты перед переменной противоположны.

Деление на показательную функцию

Деление на показательную функцию

Решение показательных неравенствПростейшие показательные неравенстваДвойные неравенстваНеравенства, решаемые вынесением за скобки степени с меньшим показателемНеравенства, решаемые заменой переменной

Простейшие показательные неравенства

Двойные неравенства

Решение показательных неравенствМетод: Вынесение за скобки степени с меньшим показателем

Решение показательных неравенствМетод: Замена переменной

Используемая литература.А.Г.Мордкович: Алгебра и начала математического анализа(профильный уровень), 10класс,2011г.А.Н. Колмогоров: Алгебра и начала математического анализа,2008г.Интернет