Презентация на тему: Основные закономерности развития информационного пространства

МЕЖДУНАРОДНЫЙ СОЛОМОНОВ УНИВЕРСИТЕТ Дмитрий Владимирович ЛАНДЭ Лекция 14“Основные закономерности развитияинформационного пространства”

Правило Парето Вильфредо Парето Анаизируя общественные процессы, Парето рассматривал социальную среду как пирамиду, наверху которой находятся немногие люди, составляющие элиту. В результате кропотливых исследований ученый сформулировал математическую зависимость между величиной дохода и количеством получающих его лиц. Ученый в 1906 году установил, что 80 процентов земли в Италии принадлежит лишь 20 процентам ее жителей. Парето пришел к выводу, что параметры полученного им распределения примерно одинаковы и не различаются принципиально в разных странах и в разное время.

Распределение Парето Распределение доходов по Парето описывается уравнением: N = A /Х p+1, где Х – величина дохода, N - численность людей с доходом, равным или выше Х, A и p - коэффициенты уравнения. В математической статистике это распределение получило имя Парето, при этом естественные ограничения на коэффициенты: Х ≥1, p > 0. Распределение Парето обладает свойством устойчивости, т.е. сумма двух случайных переменных, имеющих распределение Парето, также будет иметь это распределение. ОпределениераспределенияПарето вматематическойстатистике*: __________*Источник: Википедия

Интерпретации правила Парето Замеченное правило применимо и в очень многих областях и сформулировал правило, называемое "Закон Парето" или "Принцип 80/20". Например, при информационном поиске достаточно определить 20% необходимых ключевых слов, после чего найти 80% требуемых документов, а затем расширить поиск или воспользоваться опцией "найти похожие" для полного решения задачи. Еще один пример: 80% посещений Web-сайта приходится лишь на 20% его Web-страниц. При реализации систем массового обслуживания, в том числе и поисковых систем, необходимо учитывать то, что наиболее сложным функциональным возможностям системы, на реализацию которых ушло 80 и более процентов трудозатрат будут использоваться не более, чем 20% пользователей данной системы.

Цена 5 процентов качества Если предположить, что идеальная система имеет 100% необходимых функций, а систему, которая реализует 90% функций можно создать за 10 человеко-лет, то для доведения функциональности системы до уровня 95% потребуется еще не менее 10-ти человеко-лет. Таким образом, цена последних 5-ти процентов равна цене всей системы, работающей с функциональностью 90%. Это утверждение можно также рассматривать как следствие закона Парето в интерпретации причина-следствие. Повысить функциональность системы, работающей в 90% предельных возможностей, до 95% (следствие) потребует удвоения усилилий (причины). Конечно же соотношение 90-95 весьма приблизительно, но тенденция прекрасно видна по типовой диаграмме Парето или графику соответствующей функции распределения. Проявления эффекта 5% на практике встречаются повсеместно. Например, при появлении новых поисковых систем в Интернете. Казалось бы, вновь появившаяся система вот-вот должна превзойти такие бренды, как Yahoo! или Google и осталось совсем немного, 5-10% функциональности, можно прогнозировать, что скорее всего этого не произойдет, ведь понадобятся еще капиталовложения, превосходящие уже вложенные средства на создание "рабочей модели" новой системы.

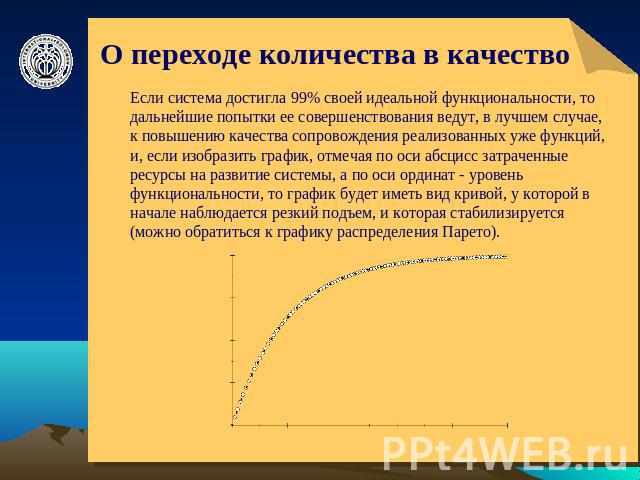
О переходе количества в качество Если система достигла 99% своей идеальной функциональности, то дальнейшие попытки ее совершенствования ведут, в лучшем случае, к повышению качества сопровождения реализованных уже функций, и, если изобразить график, отмечая по оси абсцисс затраченные ресурсы на развитие системы, а по оси ординат - уровень функциональности, то график будет иметь вид кривой, у которой в начале наблюдается резкий подъем, и которая стабилизируется (можно обратиться к графику распределения Парето).

Буква S технологического прогресса В то же время, реализация новых подходов приводит к появлению новых, даже не предполагаемых ранее показателей. В реальной жизни бывают случаи, когда после длительного процесса стабилизации происходит резкий взлет этой кривой выше уровня 100%, т.е. график принимает вид перевернутой буквы S. С чем же может быть связан такой подъем, когда функциональность резко превышает "идеальную" 100-процентную? Этот феномен обычно бывает связан с появлением новых подходов и взглядов на ставшие уже традиционными устоявшиеся процессы.

Буква S развития интернет-технологий В качестве примера этой закономерности можно привести развитие сети Интернет, которая до начала 90-х годов прошлого века рассматривалась, прежде всего, как компьютерная сеть передачи данных, а уж затем, как хранилище информационных ресурсов. Несмотря на то, что существовали такие информационные службы, как Usenet, Ftp, Gopher, до 90-х годов Сеть решала свои главные задачи, обеспечивая электронную связь между научными, общественными, государственными организациями и частными лицами. К этому времени Интернет существовал уже свыше 15-ти лет и стабилизировалась в своем развитии, в частности, по числу абонентов. Феномен появления и развития Web-технологий привел к тому, что за следующие 10 лет сеть Интернет стала крупнейшим информационным ресурсом в мире, число абонентов которой превысило миллиард человек.

Законы Зипфа При статистическом описании распределения слов по частоте их употребления в тексте (как, впрочем, и в документальных потоках) используются так называемые ранговые распределения (ранг - это, например, порядковый номер слова в списке, где все слова упорядочены по возрастанию относительных частот). Джордж Зипф экспериментально показал, что распределение слов естественного языка подчиняется закону, который можно сформулировать следующим образом. Если к какому-либо достаточно большому тексту составить список всех встретившихся в нем слов, а затем отранжировать эти слова в порядке убывания частоты их встречаемости в тексте, то для любого слова произведение его ранга и частоты встречаемости будет величиной постоянной: f * r = c, где f - частота встречаемости слова в тексте; r - ранг слова в списке; с - эмпирическая постоянная величина. Для русского и украинского языков коэффициенты Зипфа составляю приблизительно 0,06-0,07.

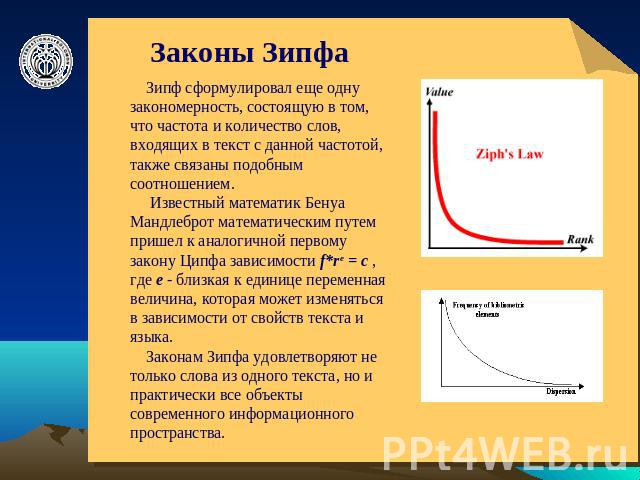
Законы Зипфа Зипф сформулировал еще одну закономерность, состоящую в том, что частота и количество слов, входящих в текст с данной частотой, также связаны подобным соотношением. Известный математик Бенуа Мандлеброт математическим путем пришел к аналогичной первому закону Ципфа зависимости f*re = c , где e - близкая к единице переменная величина, которая может изменяться в зависимости от свойств текста и языка. Законам Зипфа удовлетворяют не только слова из одного текста, но и практически все объекты современного информационного пространства.

Закономерность Брэдфорда Основной смысл закономерности С. Брэдфорда заключается в следующем: если научные журналы расположить в порядке убывания числа помещенных в них статей по конкретному предмету, то полученный список можно разбить на три зоны таким образом, чтобы количество статей в каждой зоне по заданному предмету было одина-ковым. Эти три зоны составляли: профильные журналы, посвященные рассматриваемой тематике, журналы, частично посвященные заданной области, и журналы, тематика которых весьма далека от рассматри-ваемого предмета. С. Брэдфорд установил, что количество журналов в третьей зоне будет примерно во столько раз больше, чем во второй зоне, во сколько раз число наименований во второй зоне больше, чем в ядре, т.е. P3 : P2 = P2 : P1 = N, где P1 - число журналов в 1-й зоне, P2 - во 2-й, P3 - число журналов в 3-й зоне. Закономерность Брэдфорда изначально рассматривалась как специфический случай распределения Зипфа для системы периодических изданий по науке и технике. Исходя из реалий развития сети Интернет, ее можно рассматривать как закономерность, относящуюся к ранговому распределению Web-сайтов, относительно вхождения в них Web-страниц, релевантных некоторой области знаний.

Закон Хипса В компьютерной лингвистике эмпирический закон Хипса связывает объем документа с объемом словаря уникальных слов, которые входят в этот документ. Казалось бы, словарь уникальных слов должен насыщаться, а его объем стабилизироваться при увеличении объемов текста. Оказывается это не так! В соответствии закону Хипса, эти значения связаны соотношением:v(n) = Knβ,где v – это объем словаря уникальных слов, составленный из текста, который состоит из n уникальных слов. K и β – обусловленные эмпирически параметры. Для европейских языков K принимает значение от 10 до100, а β - от 0.4 до 0.6.Закон Хипса справедлив не только для уникальных слов, но и для многих других информационных объектов, описываемых не экспоненциальной, а степенной зависимостью.

Прогноз Мура и информационная сфера Прогноз Мура родился как прогноз развития технологии микросхем. В 1965 году Гордон Мур предсказал, что плотность транзисторов в интегральных схемах и, соответственно, производительность микропроцессоров будут удваиваться каждый год. В течение трех последних десятилетий этот прогноз, названный «законом Мура», достаточно быстро был скорректирован - удвоение должно происходить каждые два года. Гордон Мур,www.intel.com

Прогноз Мура и информационная сфера Сегодня прогноз Мура распространяется на все большее количество областей. Расширение Internet, стремительный рост объемов пересыла-емых данных, развитие электронной коммерции и беспроводной связи, а также внедрение цифровых технологий в бытовую технику, можно рассматривать как следствие этого закона Мура. Было замечено, что рост документальной информации, вполне подчиняясь закону Мура, также носит экспоненциальный характер, а именно кривая роста числа документов может быть описана уравнением вида y = Aekt, где y – количество документов, t – время ; A – количество документов начале отсчета, k – коэффициент. Развитие коммуникационных возможностей приводит к росту количества доступной информации, в частности в Интернет. С другой стороны, увеличение объемов доступного контента способствует росту инновационной деятельности, все больше знаний, необходимых для исследовательских работ, публикуется в Сети, тем самым, способствуя технологическому прогрессу, на котором основывается прогноз Мура.

Спасибо за внимание! Ландэ Д.В[email protected]://poiskbook.kiev.ua МЕЖДУНАРОДНЫЙ СОЛОМОНОВ УНИВЕРСИТЕТ Киев, Украина