Презентация на тему: Нахождение объемов тел и их частей, полученных вращением плоских фигур

Презентация к серии уроков по учебному предмету «Математика» в 11-ом классе (углубленного изучения) на тему: Презентация выполнена: Леоновой Натальей Валерьевной, Учителем математики первой квалификационной категории «Основной общеобразовательной школы №9» Г. Шумихи, Курганской области МКОУ «Основная общеобразовательная школа № 9», г.Шумихи, Курганской области (Презентация рассчитана на 3 урока)

Цель урока: применение формул объёмов тел вращения для решения задач практического и прикладного характера. Задачи урока. Образовательные: - сформировать умения решать задачи на вычисление объема тел вращения и их частей; - создать условия для контроля и самоконтроля усвоения знаний; - осуществить выход на творческий уровень в ходе решения прикладных задач; Развивающие: -развивать познавательный интерес учащихся в процессе решения задач повышенной сложности и умения преодолевать трудности при их решении. -развивать любознательность, познавательный интерес, мышление и речь, внимание и память. Воспитательные: - воспитывать волю и настойчивость в достижении цели. -формировать интерес к математике и ее приложениям.

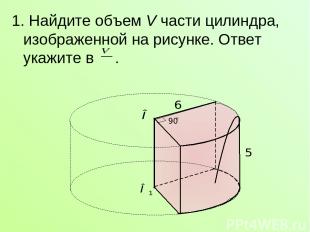
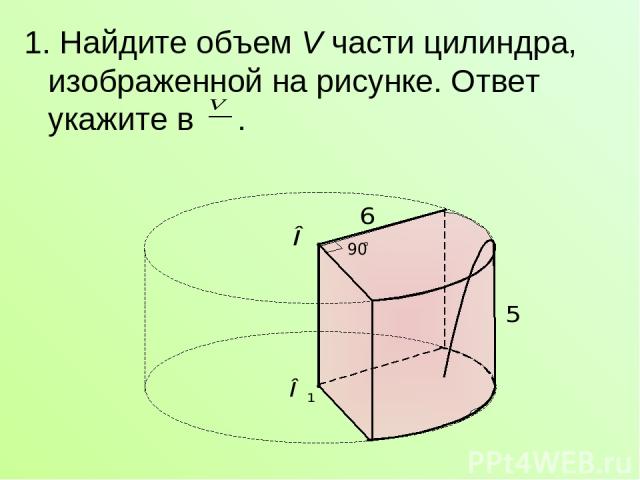
1. Найдите объем V части цилиндра, изображенной на рисунке. Ответ укажите в .

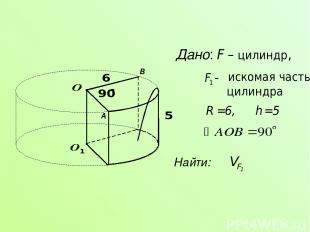
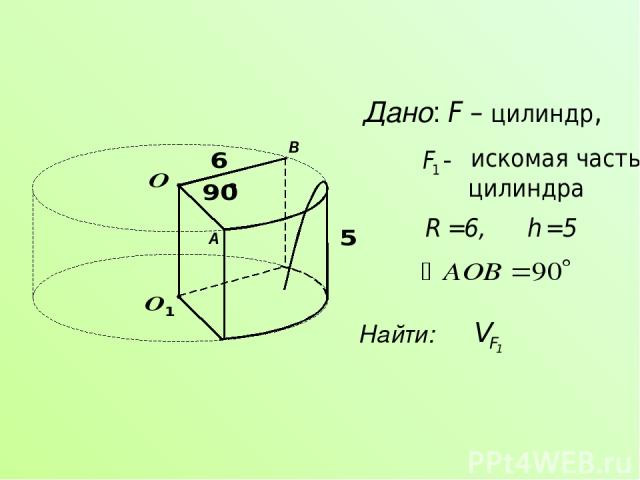
Дано: F – цилиндр, искомая часть цилиндра Найти: A B

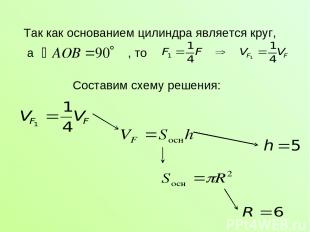
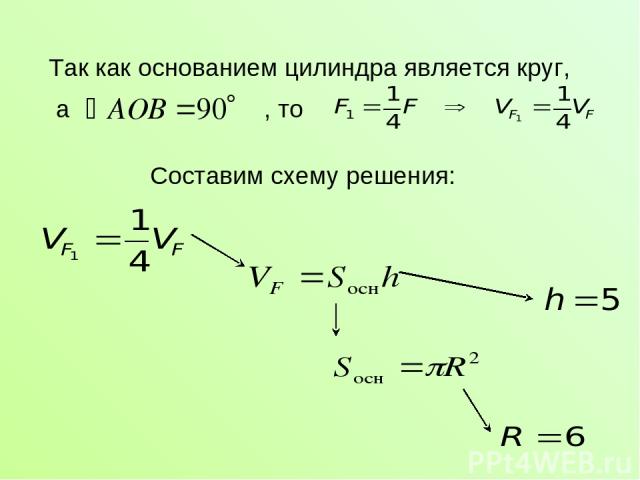
Так как основанием цилиндра является круг, а , то Составим схему решения:

Решение: Ответ: 45 Так как ответ нужно записать в виде , то

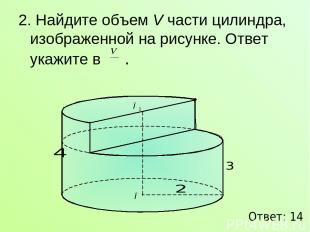
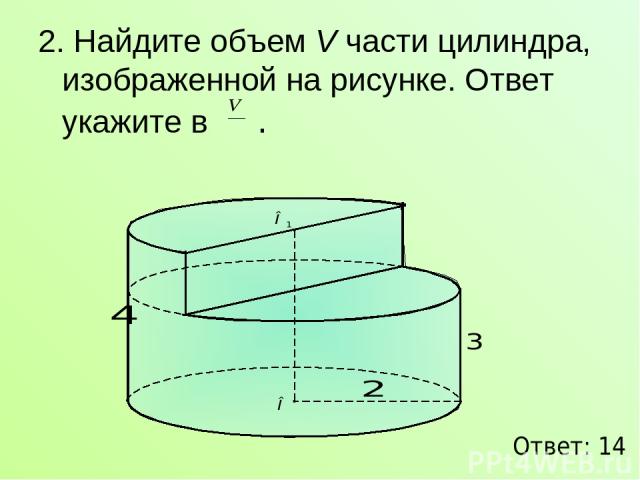
2. Найдите объем V части цилиндра, изображенной на рисунке. Ответ укажите в . Ответ: 14

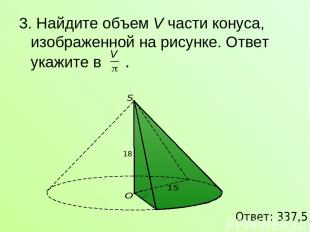
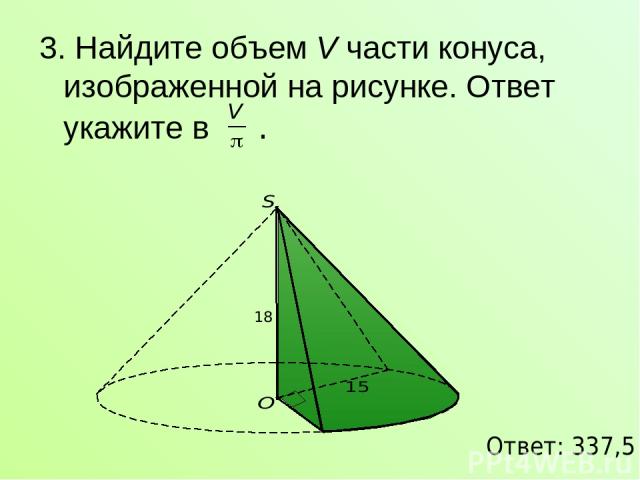
3. Найдите объем V части конуса, изображенной на рисунке. Ответ укажите в . Ответ: 337,5

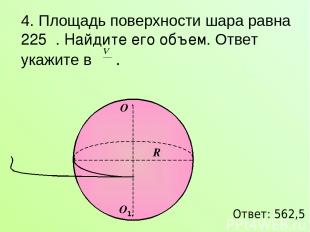
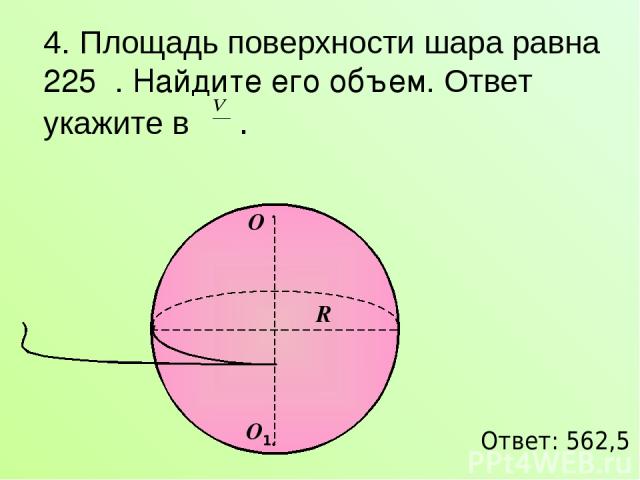
4. Площадь поверхности шара равна 225π. Найдите его объем. Ответ укажите в . Ответ: 562,5

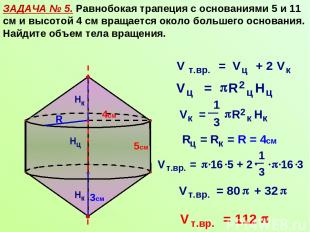
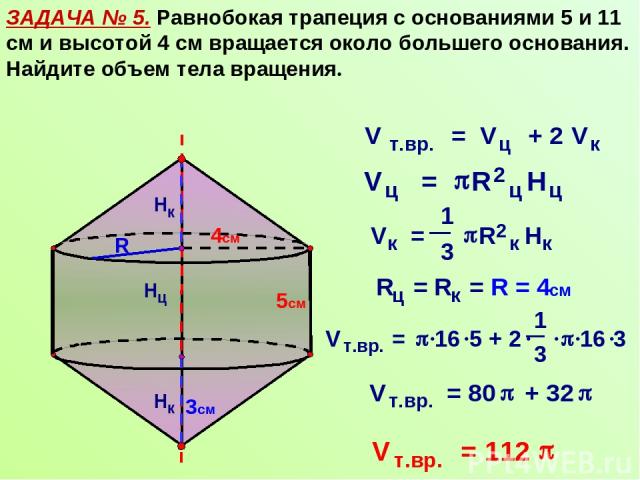
ЗАДАЧА № 5. Равнобокая трапеция с основаниями 5 и 11 см и высотой 4 см вращается около большего основания. Найдите объем тела вращения. R 5см 4см 3см

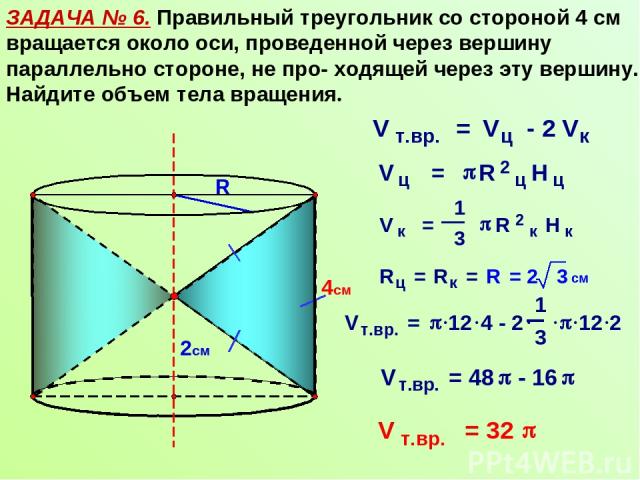
ЗАДАЧА № 6. Правильный треугольник со стороной 4 см вращается около оси, проведенной через вершину параллельно стороне, не про- ходящей через эту вершину. Найдите объем тела вращения. R 4см 2см

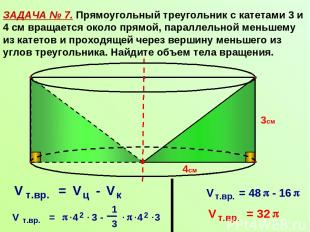
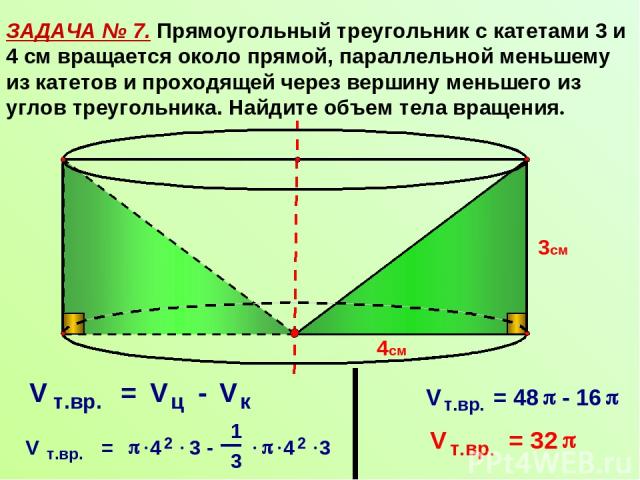
ЗАДАЧА № 7. Прямоугольный треугольник с катетами 3 и 4 см вращается около прямой, параллельной меньшему из катетов и проходящей через вершину меньшего из углов треугольника. Найдите объем тела вращения. 4см 3см

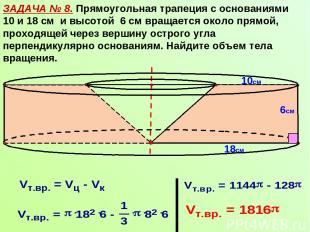
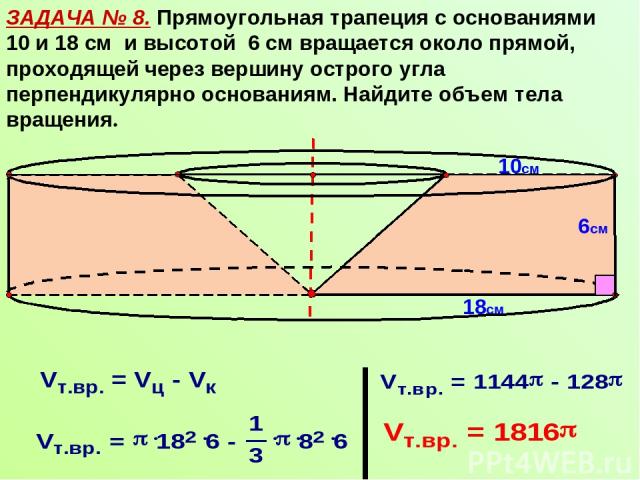
ЗАДАЧА № 8. Прямоугольная трапеция с основаниями 10 и 18 см и высотой 6 см вращается около прямой, проходящей через вершину острого угла перпендикулярно основаниям. Найдите объем тела вращения. 6см 10см 18см

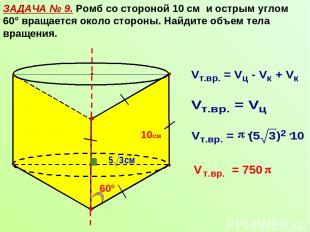
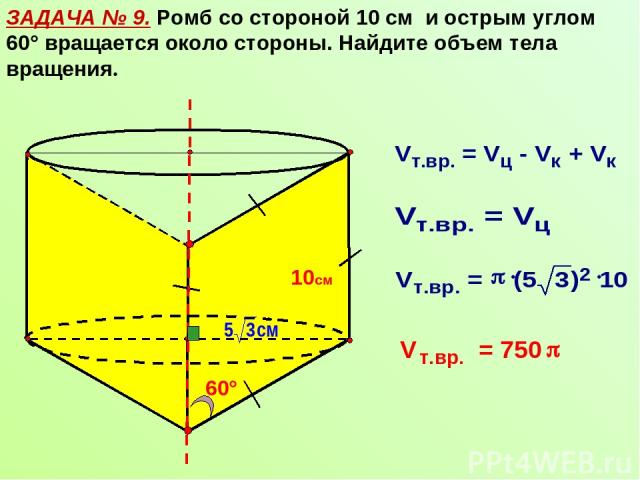
ЗАДАЧА № 9. Ромб со стороной 10 см и острым углом 60° вращается около стороны. Найдите объем тела вращения. 10см 60°

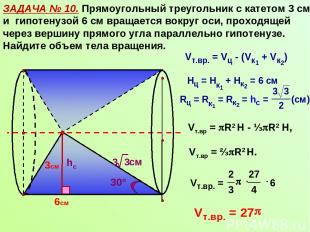
ЗАДАЧА № 10. Прямоугольный треугольник с катетом 3 см и гипотенузой 6 см вращается вокруг оси, проходящей через вершину прямого угла параллельно гипотенузе. Найдите объем тела вращения. 6см hc 30° Vт.вр = R2 Н - ⅓ R2 Н, Vт.вр = ⅔ R2 Н. 3см

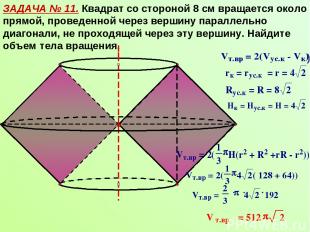
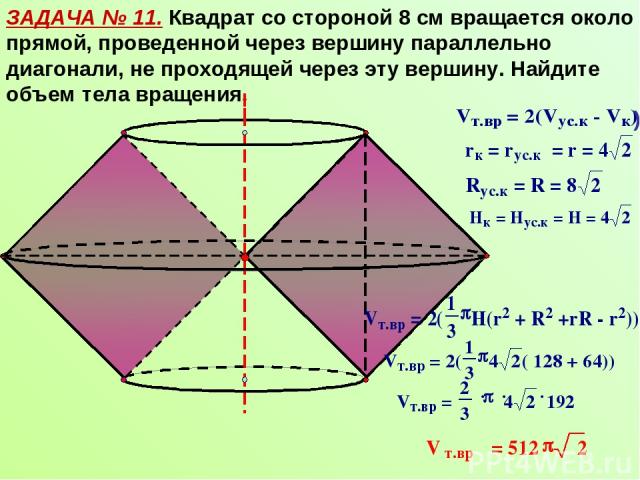
ЗАДАЧА № 11. Квадрат со стороной 8 см вращается около прямой, проведенной через вершину параллельно диагонали, не проходящей через эту вершину. Найдите объем тела вращения.

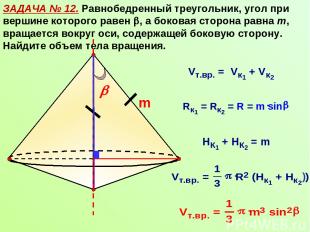
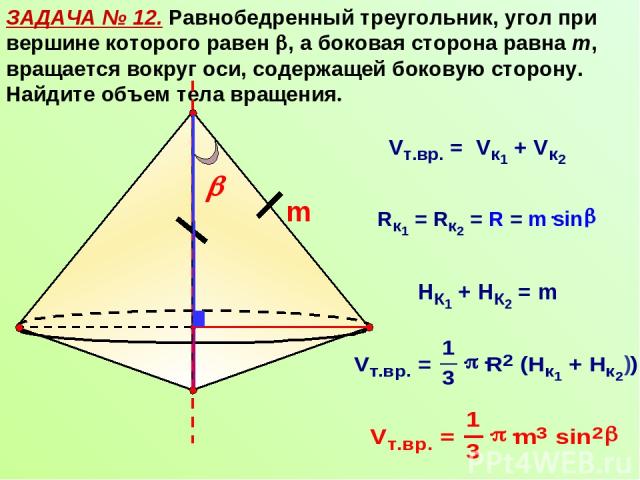
ЗАДАЧА № 12. Равнобедренный треугольник, угол при вершине которого равен , а боковая сторона равна m, вращается вокруг оси, содержащей боковую сторону. Найдите объем тела вращения. m

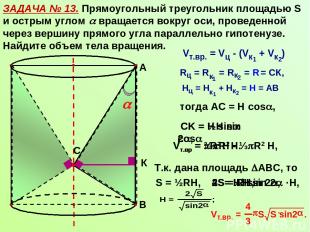
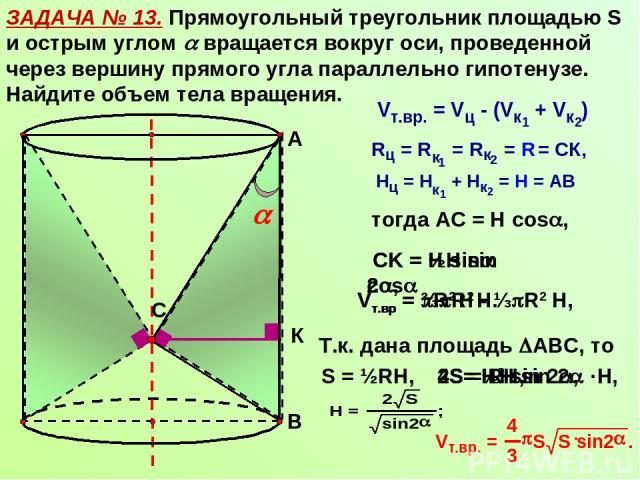
ЗАДАЧА № 13. Прямоугольный треугольник площадью S и острым углом вращается вокруг оси, проведенной через вершину прямого угла параллельно гипотенузе. Найдите объем тела вращения. С А В К тогда АС = Н cos , СK = Н sin cos Vт.вр = R2 Н - ⅓ R2 Н, Vт.вр = ⅔ R2 Н. СK = ½H sin 2 , Т.к. дана площадь АВС, то S = ½RН, 2S= ½H sin 2 ·H, 2S = RH, 4S= H2 sin 2 ,

Литература: Л.С. Атанасян, В.К. Бутузов, «Геометрия 10-11», Москва, «Просвещение» 2009 С. Б. Веселовская, В. Д. Рябчинская «Дидактические материалы по Геометрии 11», Москва, «Просвещение» 2010 П. И. Алтынов. Тесты Геометрия 10 -11классы. М. «Дрофа», 2008 И. Ф. Шарыгин, В. И. Голубев. Факультативный курс по математике. Решение задач 11 класс. М. «Просвещение», 2011 Я.И. Перельман, Занимательная геометрия.-М.: ВАП-2014. Т.М. Алешина. Сборник задач с прикладным и практическим содержанием, Москва, Профиздат- 2006 А.Д. Александров, А.Л. Вернер, В.И. Рыжик, Геометрия для 9 – 10 классов. Учебное пособие для школ и классов с углубленным изучением математики. - М., 2004 Банк открытых задач ЕГЭ http://www.fipi.ru/content/otkrytyy-bank-zadaniy-ege