Презентация на тему: Интегральное исчисление. Нахождение площадей фигур в среде Mathcad

Интегральное исчисление.Нахождение площадей фигур в среде Mathcad Преподаватель математики: Шутилина С.Н.

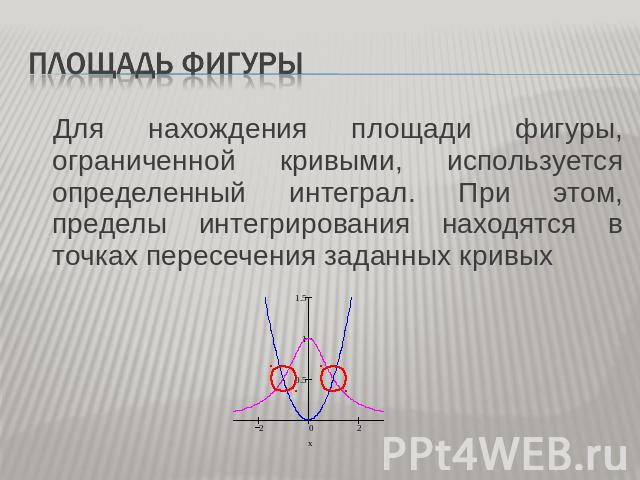
Площадь фигуры Для нахождения площади фигуры, ограниченной кривыми, используется определенный интеграл. При этом, пределы интегрирования находятся в точках пересечения заданных кривых

Работа в Mathcad В среде Mathcad для определения пределов интегрирования используется функция root(f(x),x), а для нахождения определенного интеграла – соответствующий шаблон на наборной панели Calculus

Формулировка задания Найти площадь фигуры, ограниченной кривыми:

Реализация в среде Mathcad Для определения пределов интегрирования необходимо будет построить графики обеих функций, графически определить приближенные значения, а потом, используя функцию root(f(x),x), найти точные значения пределов интегрирования Для построения графиков функций, обозначим одну функцию за f(x), а вторую за y(x)

Реализация в среде Mathcad Зададим обе функции:

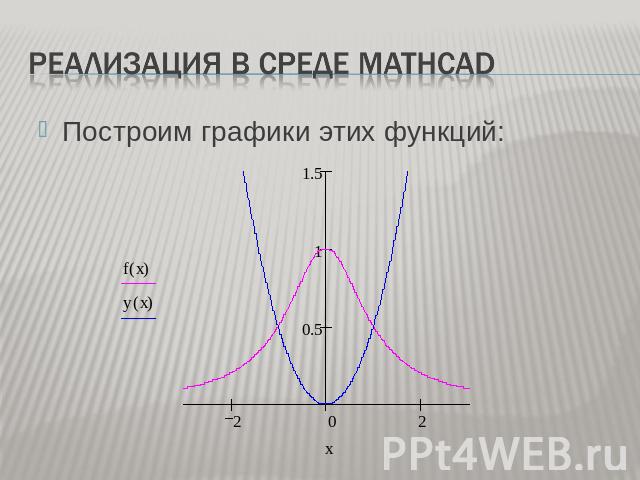
Реализация в среде Mathcad Построим графики этих функций:

Реализация в среде Mathcad По графику определилась фигура, площадь которой нужно найти: Зададим эту новую функцию в Mathcad

Реализация в среде Mathcad Также графически определились приближенные пределы интегрирования Зададим приближенное значение нижнего предела интегрирования:

Реализация в среде Mathcad Точное значение нижнего предела интегрирования найдем с помощью функции root. Будем учитывать, что вместо f(x), в функции root используется g(x):

Реализация в среде Mathcad Зададим приближенное значение верхнего предела интегрирования и найдем его точное значение:

Реализация в среде Mathcad Теперь можно найти значение интеграла фигуры g(x), ограниченной линиями f(x) и y(x):

Выводы Среда Mathcad упрощает решение сложных математических задач и позволяет использовать на занятиях по математике не только традиционные методы, но и компьютерную технику, которая облегчает вычисления. Однако, существенным недостатком решения задач с помощью Mathcad является то, что среда выводит только конечный результат, поэтому промежуточные вычисления не видны пользователю