Презентация на тему: Две замечательные теоремы планеметрии

Две замечательные теоремы планеметрии Исследовательская работа Автор: Курдюкова ЕкатеринаУченица 10 «Т»класса СОШ № 30Руководитель: Курдюкова Т. М.Учитель математики

Цель: Доказав теоремы Менелая и Чевы, исследовать их применение при решении задач.

Задачи:Показать применение теорем Менелая и Чевы при решении различных видов задач.Сравнить решения задач с использованием теорем Менелая и Чевы и традиционные решения.

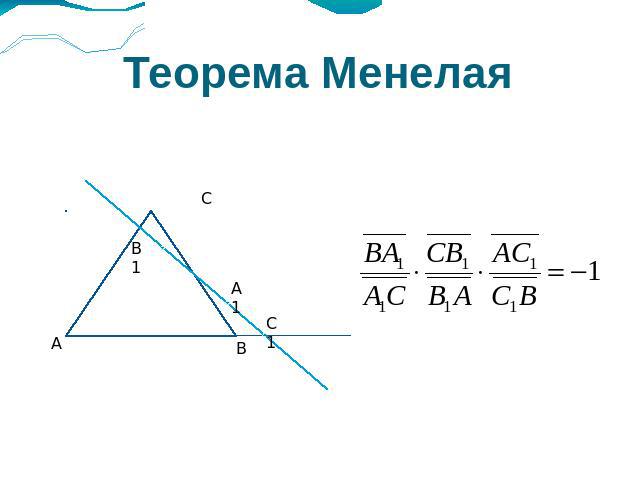
Теорема Менелая

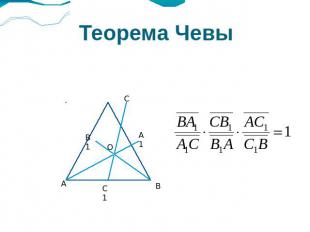
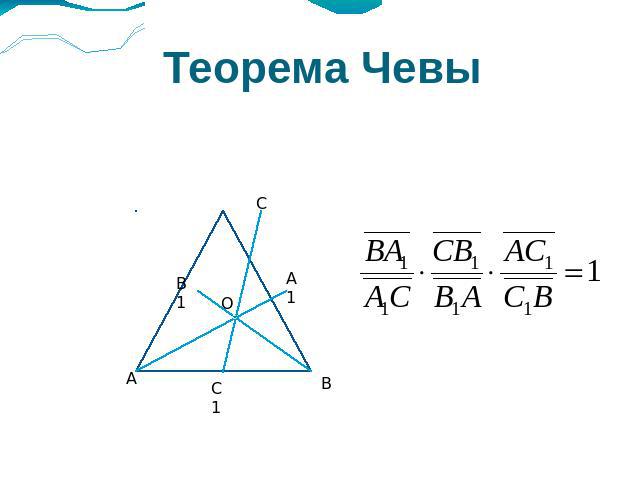
Теорема Чевы

В работе представлены задачи на… Нахождение отношения отрезков.Нахождение площадей треугольников.Доказательство принадлежности точек одной прямой.Доказательство пересечения прямых в одной точке.

Применение теоремы МенелаяОтношение отрезков.Если на чертеже имеются элементы теоремы Менелая.Если нужно доказать, что какие – либо три точки лежат на одной прямой.

На сторонах AB и AC ∆ABC взяты точки M и N так, что AM/MB=CN/NA=2. Отрезки BN и CM пересекаются в точке K. Найдите отношение отрезков BK/KN. BD || AC.∆DKB ~∆CKN, BK:KN =BD:CN.∆BMD ~∆AMC, BD:AC = BM:AM.BM:AM = 1:2,

Применение теоремы Чевы Медианы треугольника пересекаются в одной точке.Биссектрисы треугольника пересекаются в одной точке.Высоты треугольника пересекаются в одной точке.

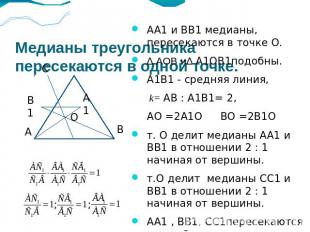
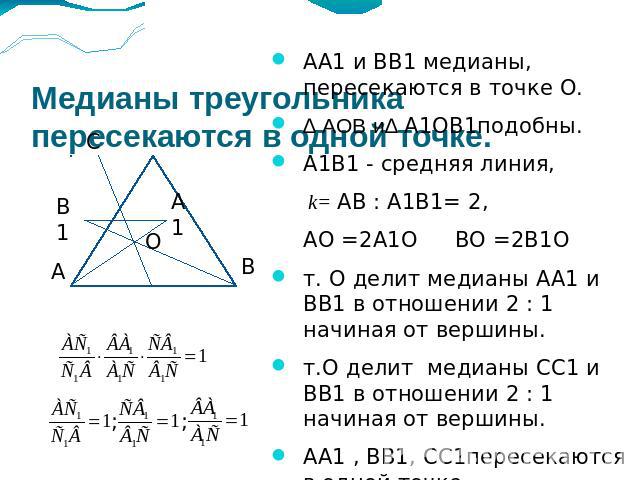
Медианы треугольника пересекаются в одной точке. АА1 и ВВ1 медианы, пересекаются в точке О.∆ АОВ и∆ А1ОВ1подобны.А1В1 - средняя линия, k= АВ : А1В1= 2,АО =2А1О ВО =2В1От. О делит медианы АА1 и ВВ1 в отношении 2 : 1 начиная от вершины.т.О делит медианы СС1 и ВВ1 в отношении 2 : 1 начиная от вершины.АА1 , ВВ1, СС1пересекаются в одной точке.

Выводы: Применение теорем полезно когда необходимо «выяснить отношения» между точками и прямыми. Позволяют добиться более простых решений.Дополнительные возможности при изучении геометрии.

Список литературы: Атанасян Л.С. «Геометрии 7-9кл»Кокейтер Г. С. М. и Грейтцер С. Л. «Новые встречи с геометрией»Прасолов В.В. «Задачи по планиметрии» Интернет ресурсы