Презентация на тему: Графики вокруг нас

Графики вокруг нас Математика - один из любимых предметов. В 7 классе изучая графики мне стало интересно - где же ещё применяются графики, оказалось, что метеорологическая служба фиксирует изменения температуры, строя с помощью термографа график температуры. Используя показания сейсмографов (приборов, непрерывно фиксирующих колебания почвы и строящих специальные графики - сейсмограммы) геологи могут предсказывать приближение землетрясения или цунами.

Врачи выявляют болезни сердца, изучая графики, полученные с помощью кардиографа, их называют кардиограммами. Широко применяются графики в экономике, в частности кривая спроса и предложения, линия производственных возможностей. Поэтому я решил изучить графики подробнее. Моя работа называется: « Графики вокруг нас». Оказывается если известен график некоторой функции y= f (x), то с помощью преобразований можно строить графики более сложных функций.

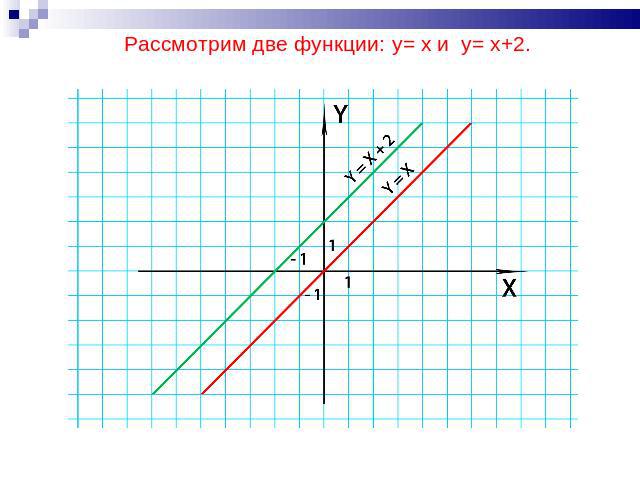
Составим таблицу Легко заметить, что значения второй функции, в каждой точке на 2 больше, чем в первой, а графики этих функций параллельны

Рассмотрим две функции: y= x и y= x+2.

Так же одним из основных назначений функций является описание реальных процессов, происходящих в природе. Но издавна ученые-философы и естествоиспытатели выделяли два типа протекания этих процессов: постепенное (непрерывное) и скачкообразное. Так, при падении тела на землю сначала происходит непрерывное нарастание скорости движения, а в момент столкновения с поверхностью земли скорость изменяется скачкообразно, становясь равной нулю или меняя направление (знак) при «отскоке» тела от земли (например, если тело - мяч).

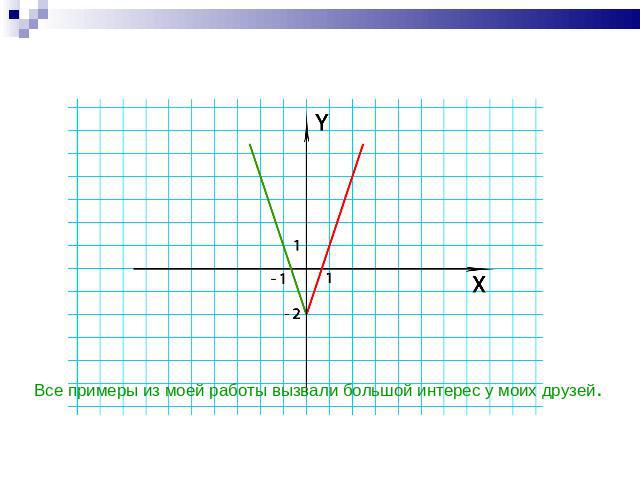
Примером служит график кусочно-элементарной функции: 3x- 2, при x больше или равно 0Y= -3x-2, при x меньше 0

Все примеры из моей работы вызвали большой интерес у моих друзей.