Презентация на тему: Символьное интегрирование и дифференцирование в пакете Mathcad, Maple V, Mathe

Символьное дифференцирование и интегрирование в пакете Maple V, Mathematica, MathCad Автор презентации: Афонькина М. Л.

Mathcad — система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается легкостью использования и применения для коллективной работы. Mathcad был задуман и первоначально написан Алленом Раздовом из Массачусетского технологического института (MIT), соучредителем компании Mathsoft, которая с 2006 года является частью корпорации PTC (Parametric Technology Corporation).
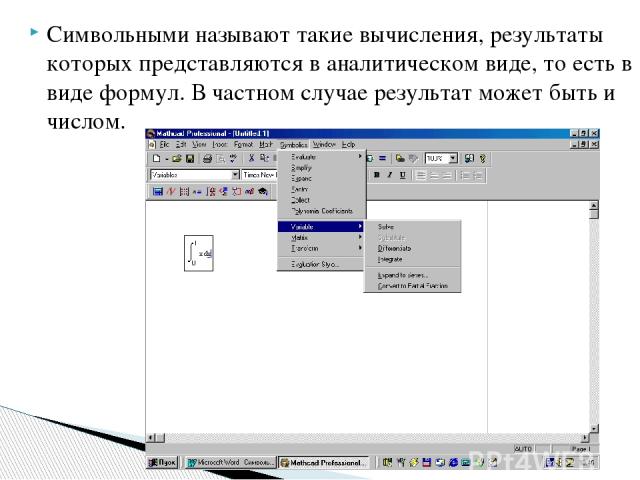
Символьными называют такие вычисления, результаты которых представляются в аналитическом виде, то есть в виде формул. В частном случае результат может быть и числом.
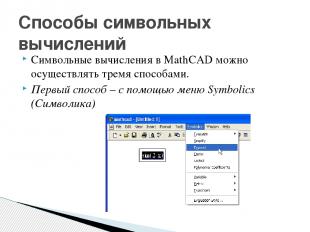
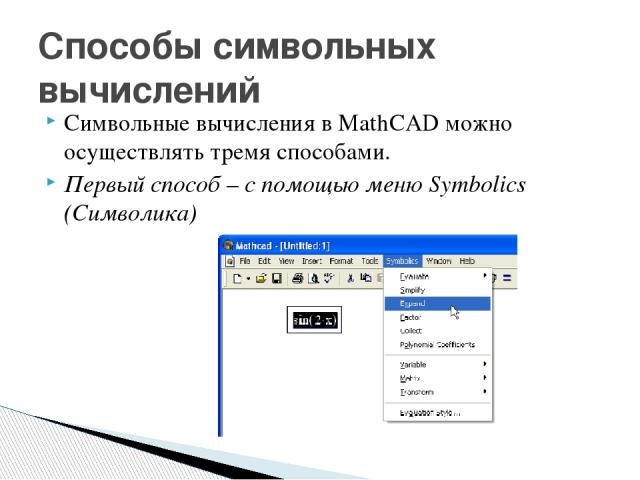
Символьные вычисления в MathCAD можно осуществлять тремя способами. Первый способ – с помощью меню Symbolics (Символика) Способы символьных вычислений

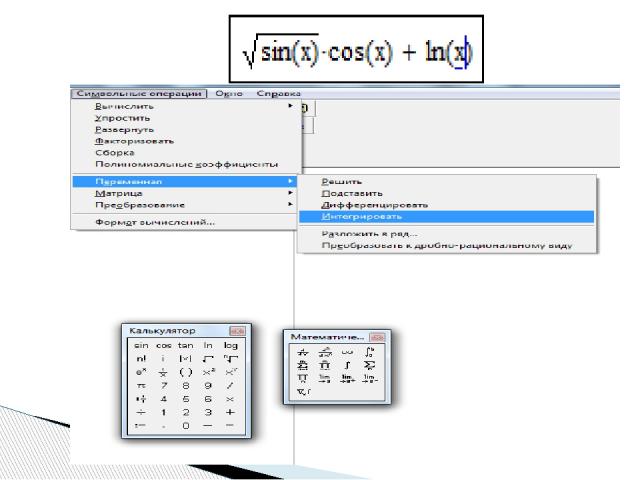
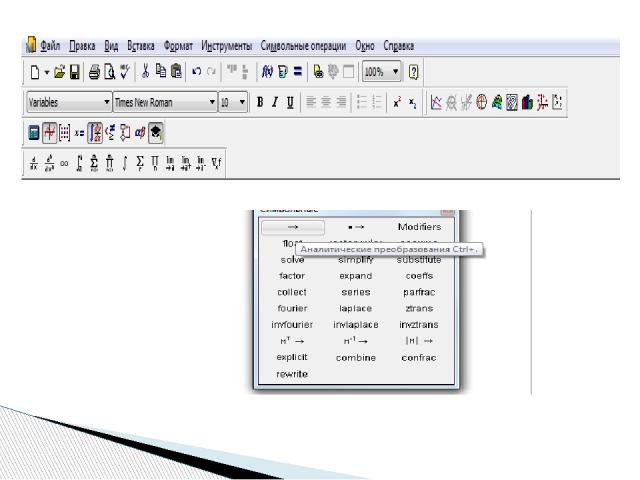
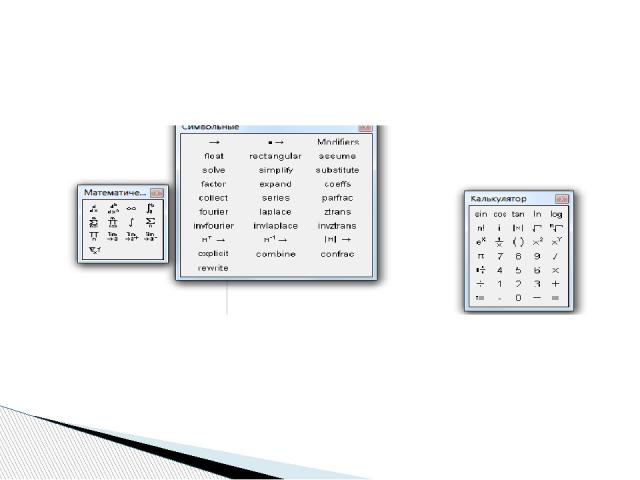
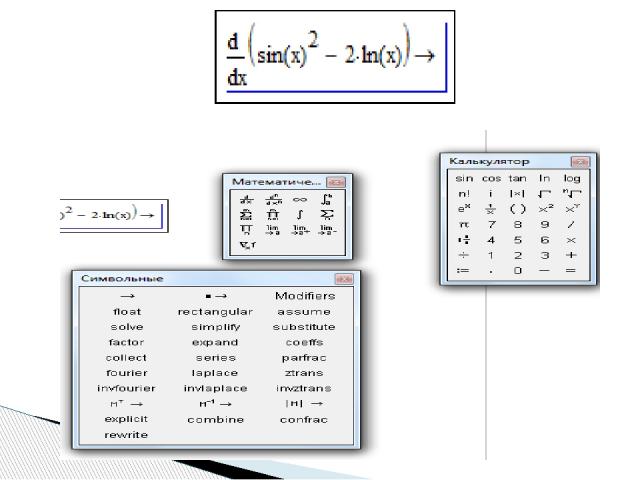
Второй способ – с помощью оператора символьного равенства , ключевых слов символьного процессора и обычных формул. Для второго способа применяются все средства MathCAD, пригодные для численных вычислений (например, панели Calculator, Evaluation и т. д.), и специальная математическая панель инструментов Symbolic (Символы), которую можно вызвать на экран нажатием кнопки Symbolic Keyword Toolbar (Символические операторы) на панели Math (Математика).

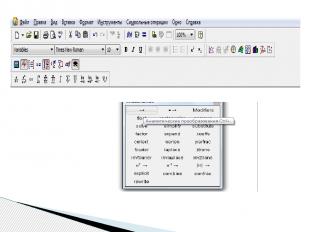
На панели Symbolic (Символы) находятся кнопки, соответствующие специфическим командам символьных преобразований

Третий способ – с помощью сочетания клавишей < Shift > + < F9 >. Если выражение не поддается аналитическим преобразованиям (либо в силу того, что задача вовсе не имеет аналитического решения, либо она оказывается слишком сложной для символьного процессора MathCAD), то в качестве результата выводится само выражение;

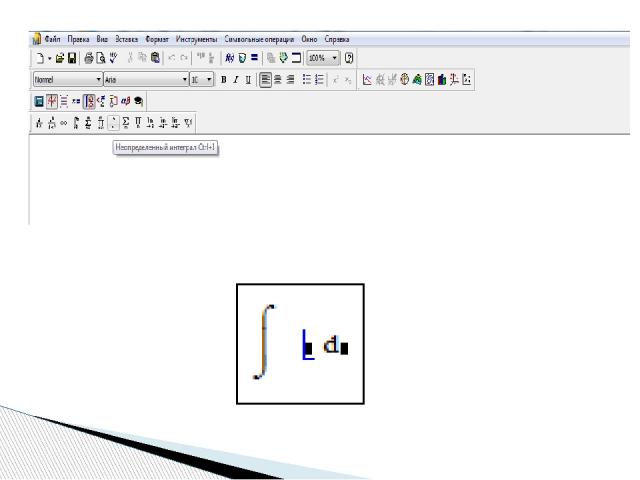
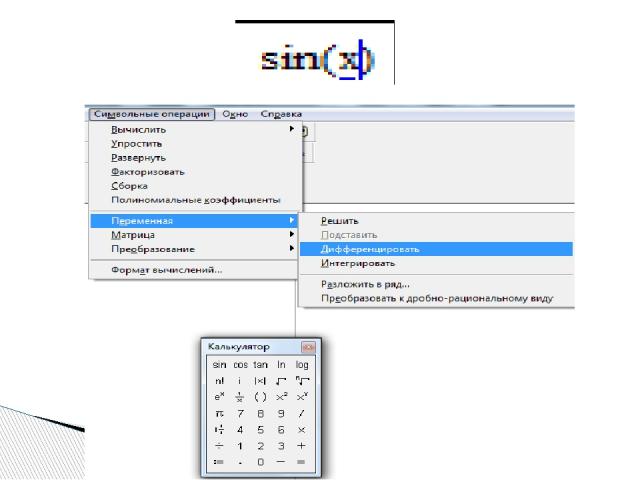
Для вычисления неопределенного интеграла от некоторого выражения по определенной переменной первым способом через меню Symbolics, нужно: - напечатать подынтегральное выражение в явном виде на экране, - поставить курсор на переменную интегрирования, - выполнить команду Symbolics/Variable/Integrate (Символика/Переменная/Интегрировать) Символьное интегрирование (Integrate)
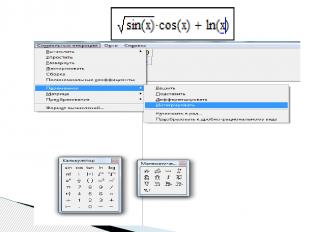

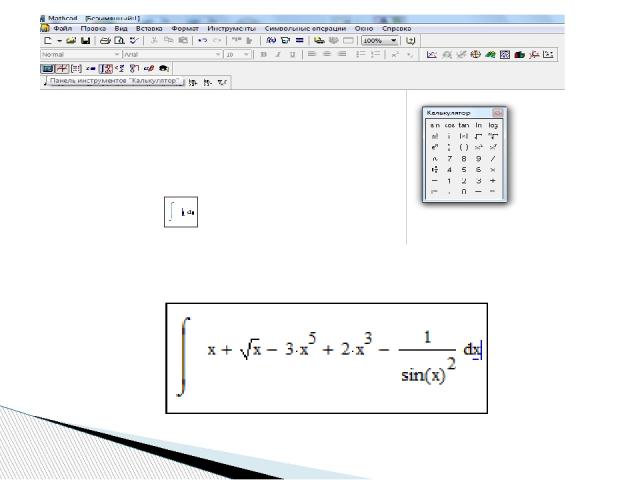
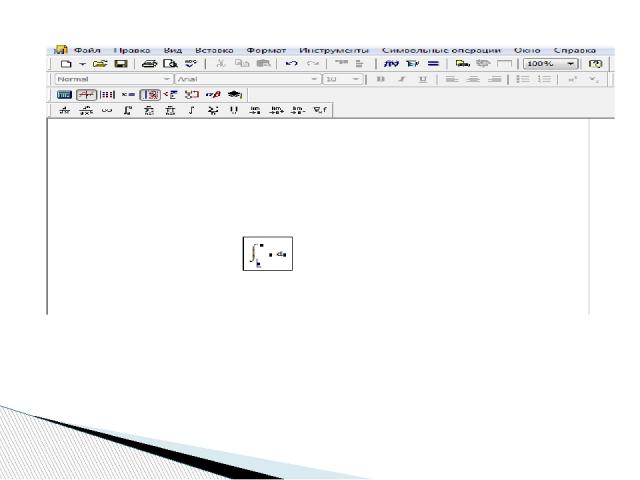
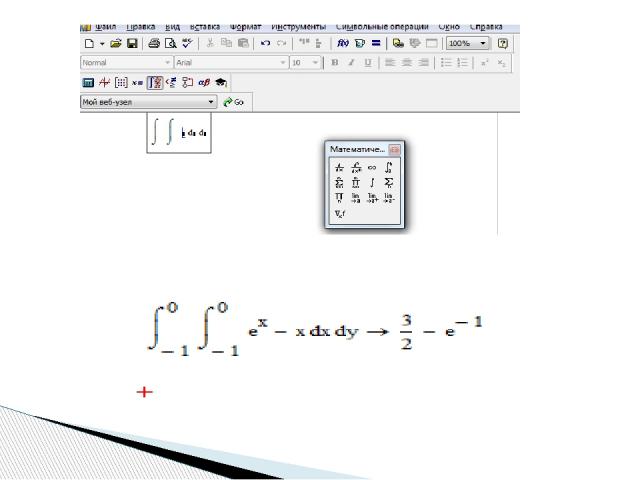
Для нахождения неопределенного интеграла вторым способом через знак символьного равенства нужно: - ввести оператор неопределенного интеграла, - в появившиеся местозаполнители ввести подынтегральное выражение (в явном или неявном виде) и переменную интегрирования, - нажать знак символьного равенства и клавишу < Enter >
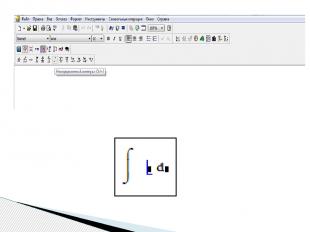
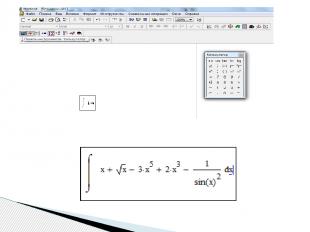

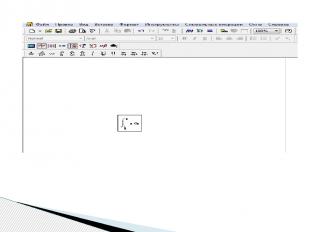
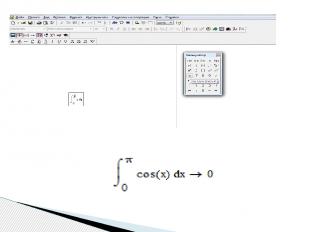
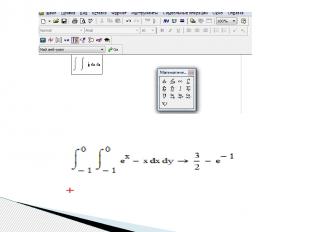

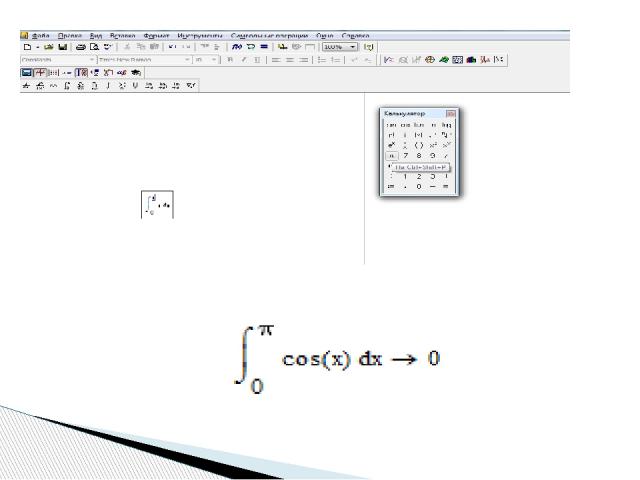
Для нахождения неопределенного интеграла третьим способом помощью сочетания клавиш < Shift > + < F9 > нужно: - ввести оператор неопределенного интеграла, - в появившиеся местозаполнители ввести переменную интегрирования и подынтегральную функцию в явном виде, - охватить все выражение выделяющей рамкой - и нажать клавиши +. Результат интегрирования появится на экране

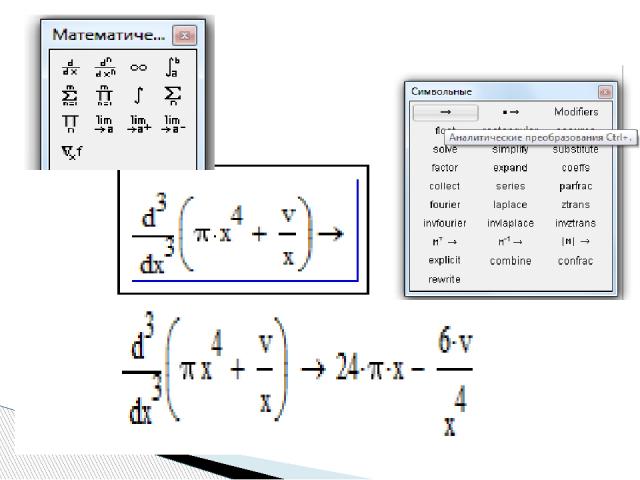
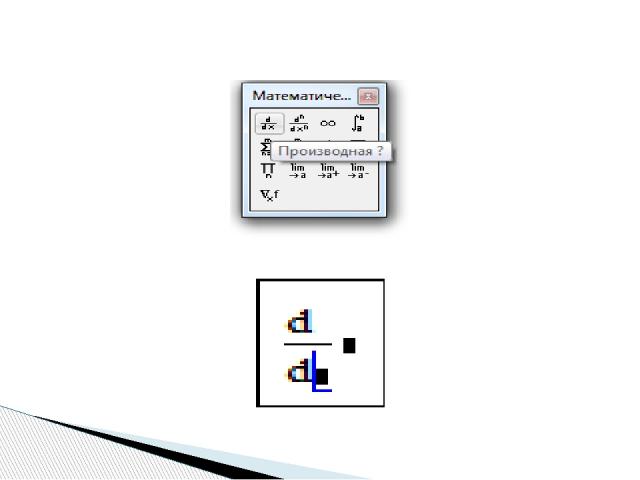
Чтобы аналитически продифференцировать выражение по некоторой переменной первым способом при помощи меню Symbolics, нужно: - напечатать дифференцируемое выражение в явном виде на экране, - поставить курсор на переменную интегрирования, - выполнить команду Symbolics/Variable/Differentiate (Символика/Переменная/Дифференцировать). В результате в следующей строке появится значение производной. Символьное дифференцирование (Differentiate)
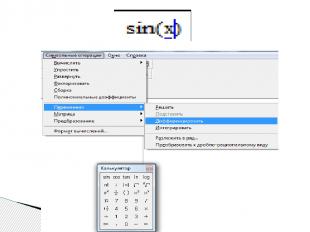


Для того чтобы найти вторую производную, нужно повторно применить эту последовательность действий, но уже к полученному результату дифференцирования. Так же находятся и производные высших порядков.
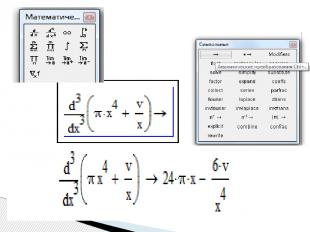

Для нахождения производной вторым способом через знак символьного равенства нужно: - ввести оператор первой производной, или оператор производной высшего порядка - в появившиеся местозаполнители ввести дифференцируемое выражение (в явном или неявном виде), порядок производной (для производных высшего порядка) и переменную интегрирования, - нажать знак символьного равенства и клавишу < Enter >
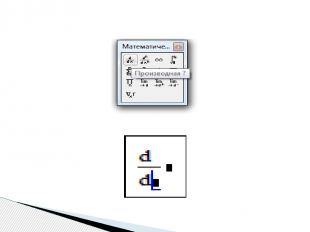
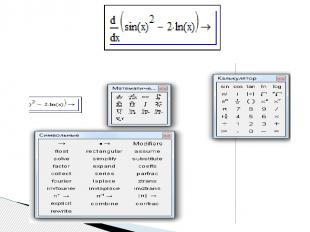
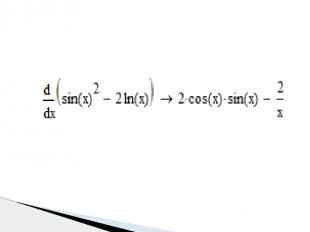

Для того чтобы вычислять производные третьим способом, используя сочетание клавиш < Shift > + < F9 >, нужно: ввести оператор дифференцирования, или оператор n-той производной, в появившиеся местозаполнители ввести переменную дифференцирования и дифференцируемую функцию в явном виде, охватить все выражение выделяющей рамкой и нажать клавиши +. Результат дифференцирования появится на экране


Maple — программный пакет, система компьютерной алгебры. Является продуктом компании Waterloo Maple Inс. (англ.)русск., которая с 1984 года выпускает программные продукты, ориентированные на сложные математические вычисления, визуализацию данных и моделирование. Система Maple предназначена для символьных вычислений, хотя имеет ряд средств и для численного решения дифференциальных уравнений и нахождения интегралов. Обладает развитыми графическими средствами. Имеет собственный язык программирования, напоминающий Паскаль.


Дифференцирование





Интегрирование


Mathematica — система компьютерной алгебры, используемая во многих научных, инженерных, математических и компьютерных областях. Изначально система была придумана Стивеном Вольфрамом, в настоящее время разрабатывается компанией Wolfram Research. Matematica

Символьные операции — это как раз то, что кардинально отличает систему Mathematica (и подобные ей символьные математические системы) от систем для выполнения численных расчетов. При символьных операциях, называемых также аналитическими, задания на вычисление составляются в виде символьных (формульных) выражений, и результаты вычислений также получаются в символьном виде. Численные результаты при этом являются частными случаями символьных.

Одна из важнейших операций — вычисление первообразных и определенных интегралов в символьном виде. Первообразная — это функция F(x), удовлетворяющая уравнению где С — постоянная интегрирования. А вычисление определенного интеграла с пределами — верхним b и нижним а — производится по формуле

Заметим, что определенный интеграл может быть представлен как аналитическим, так « численным значением. Для вычисления численных значений определенных интегралов разработан ряд приближенных методов — от простых (прямоугольников и трапеций) до сложных, автоматически адаптирующихся к характеру изменения подынтегральной функции f(x).

Для интегрирования в системе Mathematica используются следующие функции: Integrate [f, x] — возвращает первообразную (неопределенный интеграл) подынтегральной функции f по переменной х; Integrate [f, {x, xmin, xmax}] — возвращает значение определенного интеграла с пределами от x min до x max ;Integrate [f, {x, xmin, xmax}, {у, ymin, ymax},...] —возвращает значение кратного интеграла с пределами от x min до x max по переменной х, от y min до y max по переменной у и т. д. (кратность реально не ограничена).

Обычно функция Integrate применяется в простейшей форме, но она имеет три характерные опции: Options[Integrate] {Assumptions -> {}, GenerateConditions->Automatic, PrincipalValue > False)

Для обозначения бесконечных пределов используется константа Infinity. Эта константа означает положительную бесконечность, для задания отрицательной бесконечности она используется со знаком «минус». Особый интерес, естественно, вызывает применение функции Integrate для вычисления заданных пользователем неопределенных интегралов в символьном виде.

Здесь входная ячейка в первом примере представлена в формате ввода (Input-Form), а в остальных примерах — в стандартном формате (StandardForm). При записи интегралов последний предпочтителен ввиду большей наглядности, поскольку при этом знаки интеграла имеют естественный математический вид
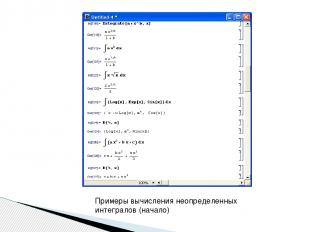
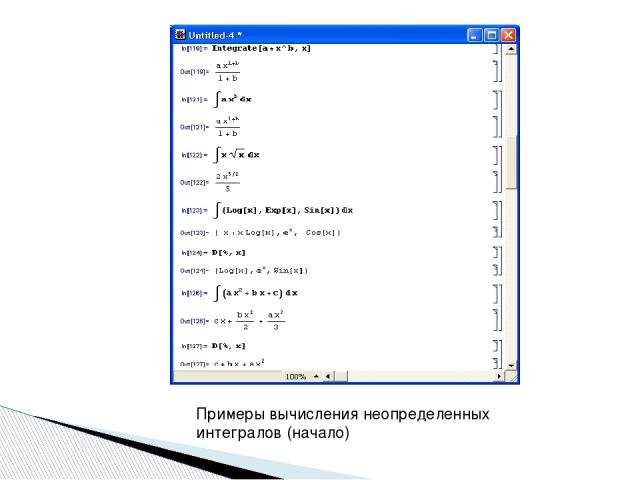
Примеры вычисления неопределенных интегралов (начало)

Примеры вычисления неопределенных интегралов (продолжение)
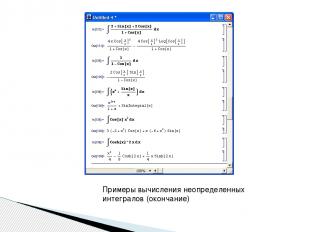
Примеры вычисления неопределенных интегралов (окончание)
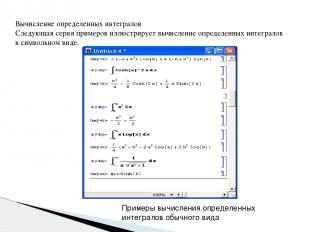
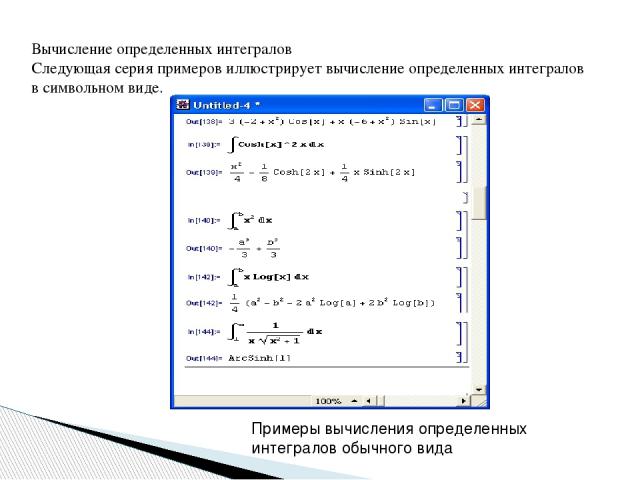
Вычисление определенных интегралов Следующая серия примеров иллюстрирует вычисление определенных интегралов в символьном виде. Примеры вычисления определенных интегралов обычного вида
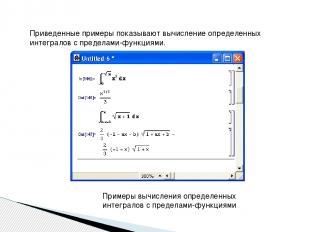
Приведенные примеры показывают вычисление определенных интегралов с пределами-функциями. Примеры вычисления определенных интегралов с пределами-функциями

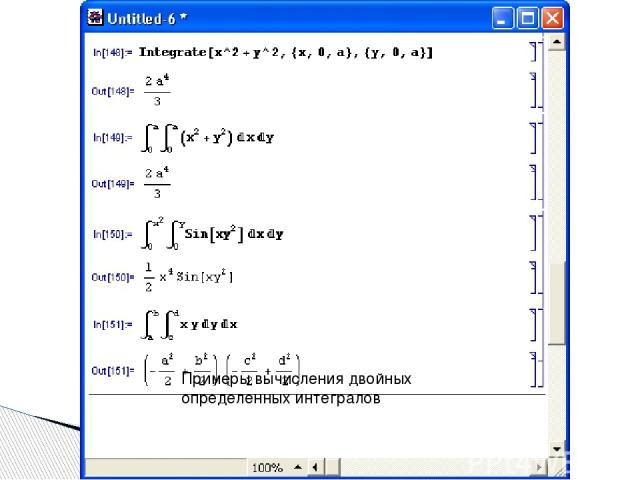
Mathematica способна вычислять даже кратные интегралы с фиксированными и переменными верхним или нижним пределами. Кратный, например двойной, интеграл с фиксированными пределами имеет вид:
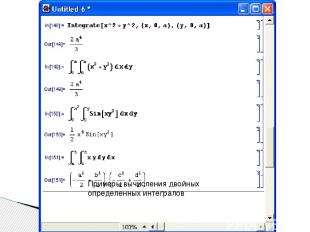
Примеры вычисления двойных определенных интегралов

Другая серия примеров показывает, как вычисляются двойные и тройные интегралы, пределы которых сами по себе являются функциями.

При проведении математических и технических расчетов именно операции математического анализа используются чаще всего. Одна из основных операций математического анализа — дифференцирование. Mathematica умеет вычислять производные всех стандартных математических функций, а также специальных функций (А. Н. Прокопеня и А. В. Чичурин) Дифференцирование

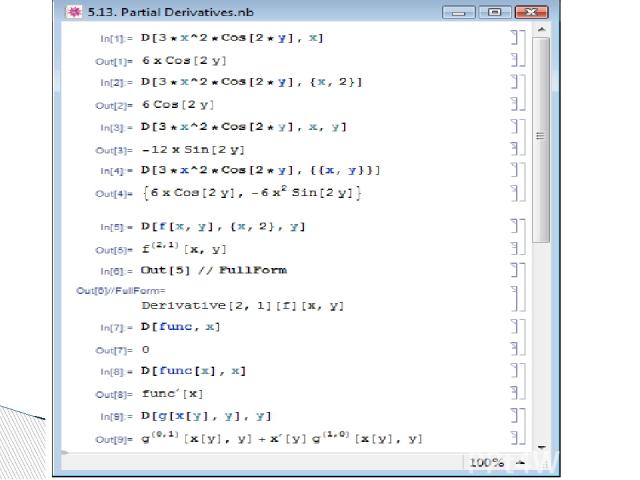
Производную первого порядка функции expr по переменной var вычисляют при помощи выражения D[expr,var]. При вычислении смешанных и кратных производных аргумент var задаётся в виде списка. Производную высшего порядка n вычисляют при помощи функции D[expr,{var,n}], а производную по нескольким переменным var1,var2,... — при помощи D[expr,var1,var2,...]
![Функция D[expr,{{var1,var2,...}}] для скалярного выражения expr даёт вектор прои Функция D[expr,{{var1,var2,...}}] для скалярного выражения expr даёт вектор прои](https://fs3.ppt4web.ru/images/132018/191238/310/img57.jpg)
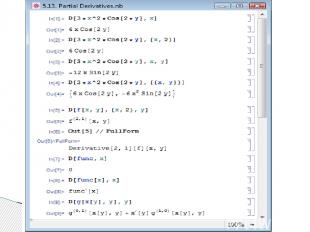
Функция D[expr,{{var1,var2,...}}] для скалярного выражения expr даёт вектор производныхexpr по каждой из переменных var1,var2,... (пример In[4]).
![Рассмотрим произвольную функцию f[x,y] и вычислим ее третью смешанную производну Рассмотрим произвольную функцию f[x,y] и вычислим ее третью смешанную производну](https://fs3.ppt4web.ru/images/132018/191238/310/img58.jpg)
Рассмотрим произвольную функцию f[x,y] и вычислим ее третью смешанную производную \partial ^3f/\partial х^2\partial у. Обозначение производной в Out[5] задано выражением (2,1), компоненты которого показывают, что вычислена вторая производная по первому аргументу и первая производная по второму аргументуЕсли Mathematica не может явно вычислить производную, она сводит вычисление к выражениям с видом Derivative[n1,n2,...][f]. В примере In представлена внутренняя форма вычисленного выражения Out[5].

Если выражение, к которому применена функция дифференцирования, не содержит переменных, по которым дифференцирование осуществляется, то Mathematica D рассматривает это выражение как константу по переменным дифференцирования. Поэтому при вычислении производной некоторой функции необходимо обязательно в явном виде указывать её аргумент. Если в функции двух аргументов один аргумент зависит от другого, например, , то эту зависимость также следует явно указывать .
![В Mathematica имеется функция Dt[expr,var], которая находит полную производную в В Mathematica имеется функция Dt[expr,var], которая находит полную производную в](https://fs3.ppt4web.ru/images/132018/191238/310/img61.jpg)
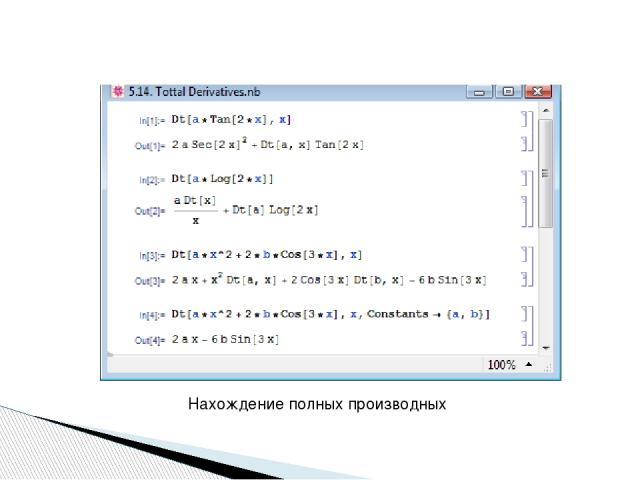
В Mathematica имеется функция Dt[expr,var], которая находит полную производную выражения expr: она рассматривает все символы в выражении expr как функции от переменных var, по которым осуществляется дифференцирование.. Функция в упрощённом виде, без второго аргумента, Dt[expr], есть дифференциал выражения expr — пример In[2].

Если дифференцируемое выражение expr содержит какие-либо константы, т.е., при дифференцировании их производные равны нулю, то их можно указать в соответствующей опции, т.е., задать функцию дифференцирования в виде Dt[expr,var,Constants->{const1,const2,...}], где {const1,const2,...} — список имеющихся в выражении expr констант .
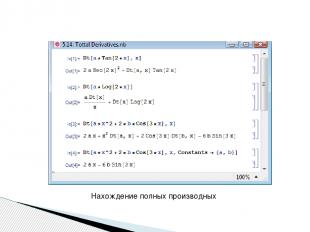
Нахождение полных производных














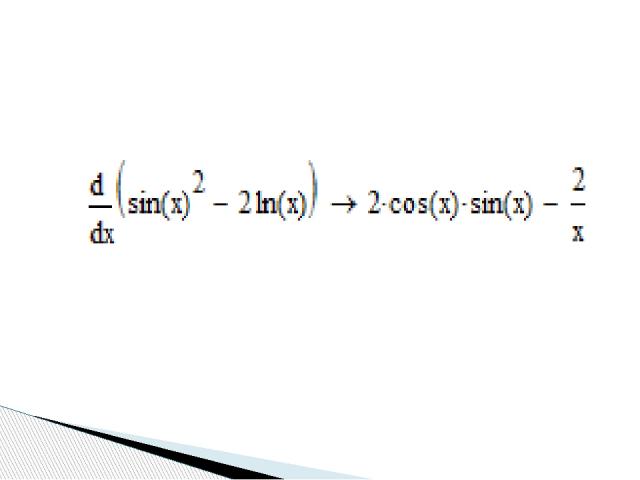















![Для интегрирования в системе Mathematica используются следующие функции: Integrate [f, x] — возвращает первообразную (неопределенный интеграл) подынтегральной функции f по переменной х; Integrate [f, {x, xmin, xmax}] — возвращает значение определенн… Для интегрирования в системе Mathematica используются следующие функции: Integrate [f, x] — возвращает первообразную (неопределенный интеграл) подынтегральной функции f по переменной х; Integrate [f, {x, xmin, xmax}] — возвращает значение определенн…](https://fs3.ppt4web.ru/images/132018/191238/640/img43.jpg)
![Обычно функция Integrate применяется в простейшей форме, но она имеет три характерные опции: Options[Integrate] {Assumptions -> {}, GenerateConditions->Automatic, PrincipalValue > False) Обычно функция Integrate применяется в простейшей форме, но она имеет три характерные опции: Options[Integrate] {Assumptions -> {}, GenerateConditions->Automatic, PrincipalValue > False)](https://fs3.ppt4web.ru/images/132018/191238/640/img44.jpg)








![Производную первого порядка функции expr по переменной var вычисляют при помощи выражения D[expr,var]. При вычислении смешанных и кратных производных аргумент var задаётся в виде списка. Производную высшего порядка n вычисляют при помощи функции D[e… Производную первого порядка функции expr по переменной var вычисляют при помощи выражения D[expr,var]. При вычислении смешанных и кратных производных аргумент var задаётся в виде списка. Производную высшего порядка n вычисляют при помощи функции D[e…](https://fs3.ppt4web.ru/images/132018/191238/640/img56.jpg)
![Функция D[expr,{{var1,var2,...}}] для скалярного выражения expr даёт вектор производныхexpr по каждой из переменных var1,var2,... (пример In[4]). Функция D[expr,{{var1,var2,...}}] для скалярного выражения expr даёт вектор производныхexpr по каждой из переменных var1,var2,... (пример In[4]).](https://fs3.ppt4web.ru/images/132018/191238/640/img57.jpg)
![Рассмотрим произвольную функцию f[x,y] и вычислим ее третью смешанную производную \partial ^3f/\partial х^2\partial у. Обозначение производной в Out[5] задано выражением (2,1), компоненты которого показывают, что вычислена вторая производная по перв… Рассмотрим произвольную функцию f[x,y] и вычислим ее третью смешанную производную \partial ^3f/\partial х^2\partial у. Обозначение производной в Out[5] задано выражением (2,1), компоненты которого показывают, что вычислена вторая производная по перв…](https://fs3.ppt4web.ru/images/132018/191238/640/img58.jpg)

![В Mathematica имеется функция Dt[expr,var], которая находит полную производную выражения expr: она рассматривает все символы в выражении expr как функции от переменных var, по которым осуществляется дифференцирование.. Функция в упрощённом виде, без… В Mathematica имеется функция Dt[expr,var], которая находит полную производную выражения expr: она рассматривает все символы в выражении expr как функции от переменных var, по которым осуществляется дифференцирование.. Функция в упрощённом виде, без…](https://fs3.ppt4web.ru/images/132018/191238/640/img61.jpg)