Презентация на тему: ПРЕЗЕНТАЦИЯ ПО ИНФОРМАТИКЕ

Тема 1.5 Основные понятия алгебры логики
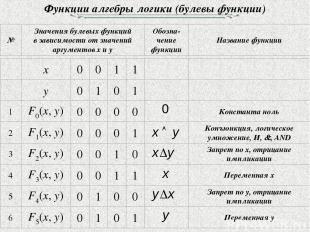
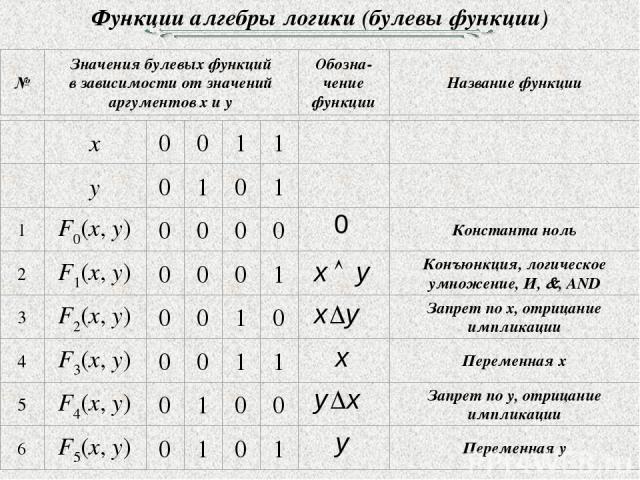
Функции алгебры логики (булевы функции)
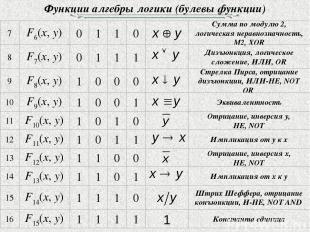
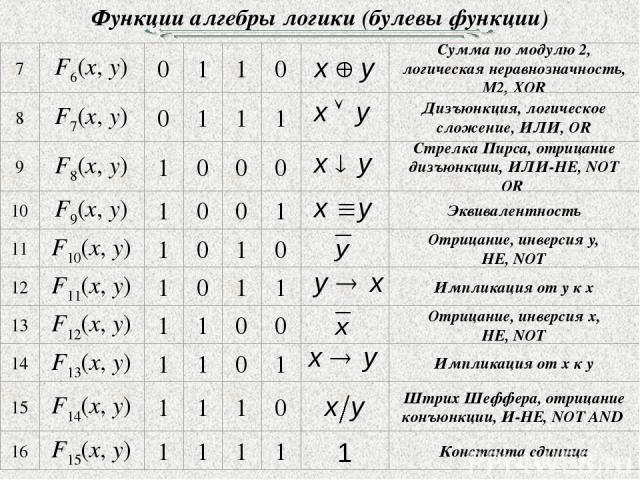
Функции алгебры логики (булевы функции)

Основные законы алгебры логики

Основные законы алгебры логики 5) Законы дополнительности: 8) Дистрибутивные законы (законы распределения):

Основные законы алгебры логики 11) Законы де Моргана (законы инверсии):
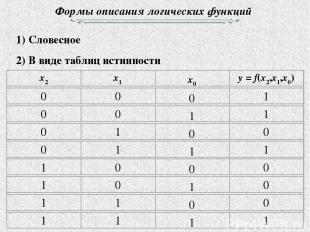
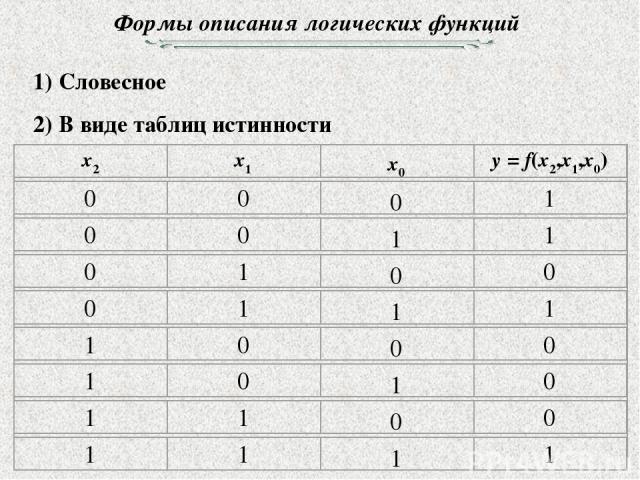
Формы описания логических функций 1) Словесное 2) В виде таблиц истинности

Формы описания логических функций 3) В виде последовательности десятичных чисел 4) В виде алгебраических выражений. Операция замены аргументов одной функции другими, более простыми функциями называется суперпозицией функций F(x2,x1,x0) = (1,2,4,7) = (1,2,4,7) F(x2,x1,x0) = (0,3,5,6) = (0,3,5,6) Элементарная конъюнкция Элементарная дизъюнкция
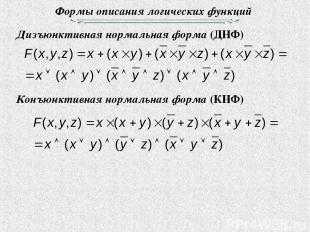
Формы описания логических функций Дизъюнктивная нормальная форма (ДНФ) Конъюнктивная нормальная форма (КНФ)

Если в состав логического выражения входят наборы элементарных конъюнкций с одинаковым количеством переменных, связанные дизъюнкцией, то такая форма ФАЛ называется совершенной дизъюнктивной нормальной формой (СДНФ) Если в состав логического выражения входят наборы элементарных дизъюнкций с одинаковым количеством переменных, связанные конюнкцией, то такая форма ФАЛ называется совершенной конъюнктивной нормальной формой (СКНФ)
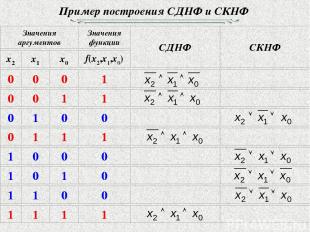
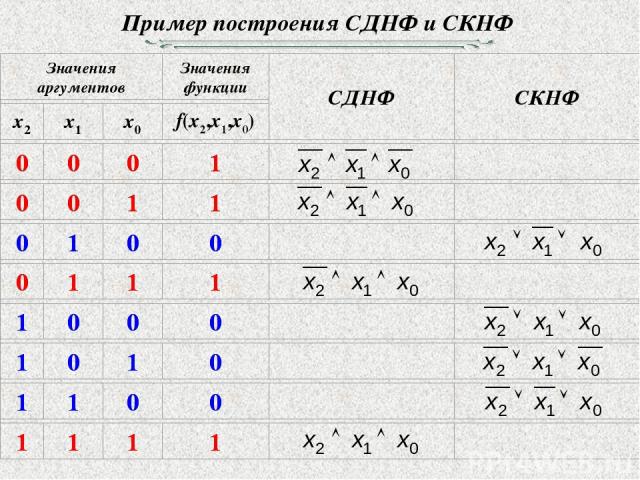
Пример построения СДНФ и СКНФ

Пример построения СДНФ и СКНФ СДНФ СКНФ
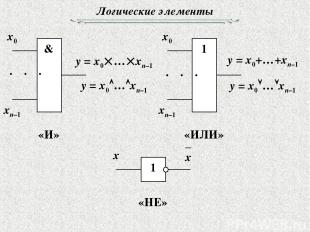
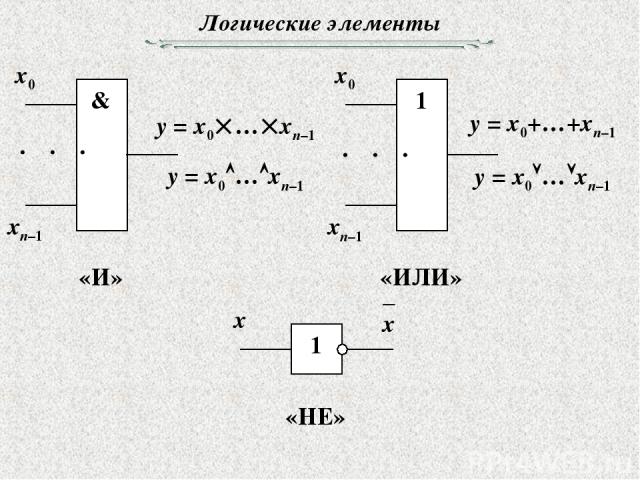
Логические элементы
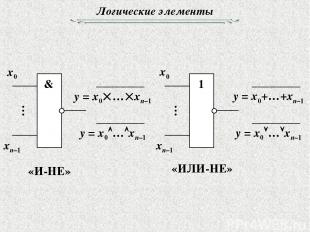
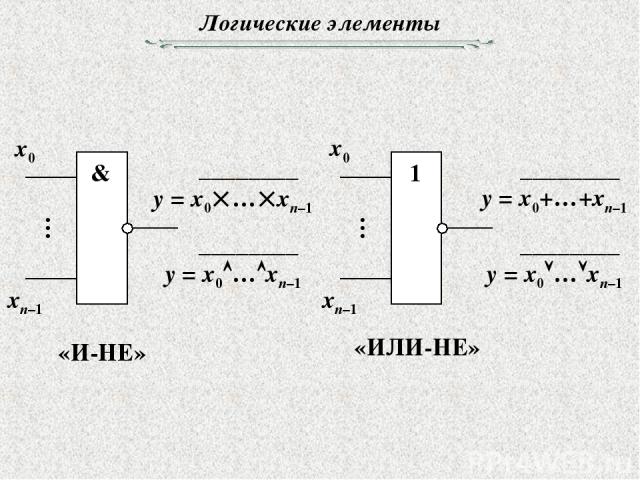
Логические элементы

Тема 1.6 Логические основы ЭВМ

Минимизация булевых функций Метод непосредственных преобразований

Минимизация булевых функций Метод непосредственных преобразований Для ранее построенной СДНФ

Для ранее построенной СКНФ

Минимизация булевых функций Метод Карно-Вейча 1 1 0

Минимизация булевых функций Метод Карно-Вейча

Свойства карты Карно: комбинации значений переменных для соседних клеток карты Карно различаются значением только одной входной переменной. При переходе с одной клетки в соседнюю клетку всегда изменяется значение только одной переменной на ее инверсное значение; соседними являются между собой крайние левые и крайние правые клетки карты, а также крайние верхние и крайние нижние клетки (как если бы карты были свернуты в цилиндры по вертикали и горизонтали).

Все единицы (при записи функции в дизъюнктивной форме) и все нули (при записи функции в конъюнктивной форме) должны быть замкнуты в прямоугольные контуры. Единичные контуры могут содержать несколько единиц, но не должны содержать нулей. Нулевые контуры могут содержать несколько нулей, но не должны содержать единиц. Одноименные контуры могут накладываться один на другой, т.е. одна и та же единица (или ноль) может входить в несколько единичных (нулевых) контуров. Число клеток в контуре должно быть равно 2i , где i = 0, 1, 2, …, n, т.е. число клеток в контуре выражается числами 0, 1, 2, 4, 8, 16, 32, … Каждой единичной клетке отвечает конъюнкция входных переменных, которые определяют данную клетку. Каждой нулевой клетке отвечает дизъюнкция инверсий входных переменных, которые определяют данную клетку. Выражения, которые отвечают контурам, не содержат тех переменных, чьи границы пересекаются площадью, ограниченной данным контуром. Дизъюнктивная форма ФАЛ составляется в виде дизъюнкций конъюнкций, которые отвечают единичным контурам. Конъюнктивная форма ФАЛ составляется в виде конъюнкций дизъюнкций, которые отвечают нулевым контурам. Если каждой клетке отвечает свой контур, то результирующее выражение представляет собой СДНФ или СКНФ данной ФАЛ. Минимальной ДНФ или КНФ отвечает минимальное количество единичных или нулевых контуров.

Минимизация булевых функций Метод Карно-Вейча Минимальная ДНФ: Минимальная КНФ: F(x2, x1, x0) = y1 y2
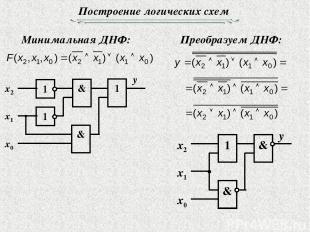
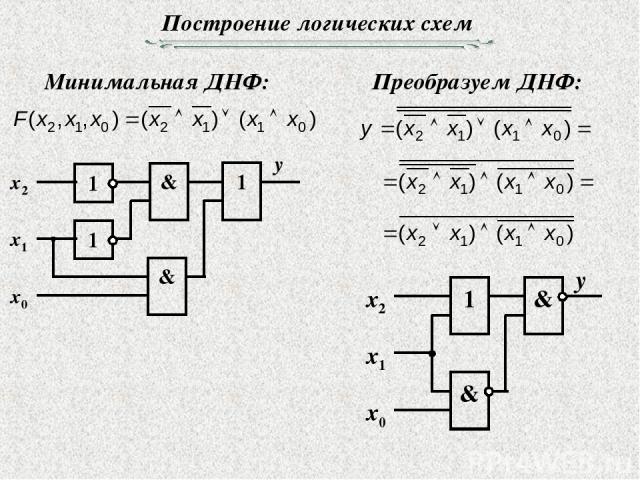
Построение логических схем Минимальная ДНФ: Преобразуем ДНФ:
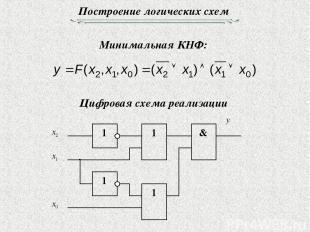
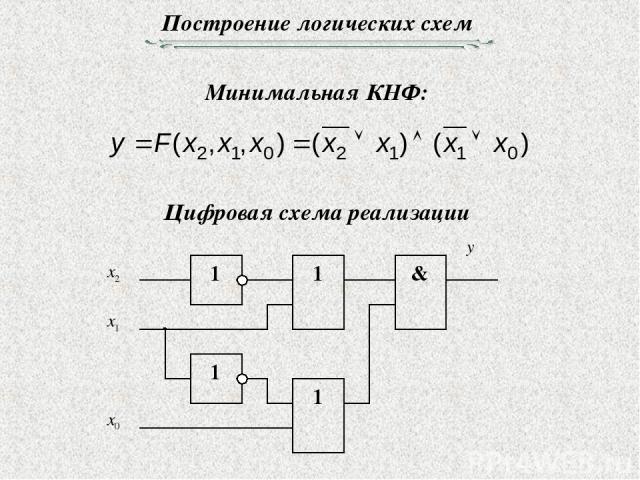
Построение логических схем Минимальная КНФ: Цифровая схема реализации
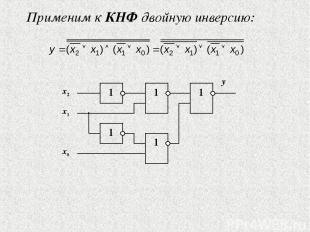
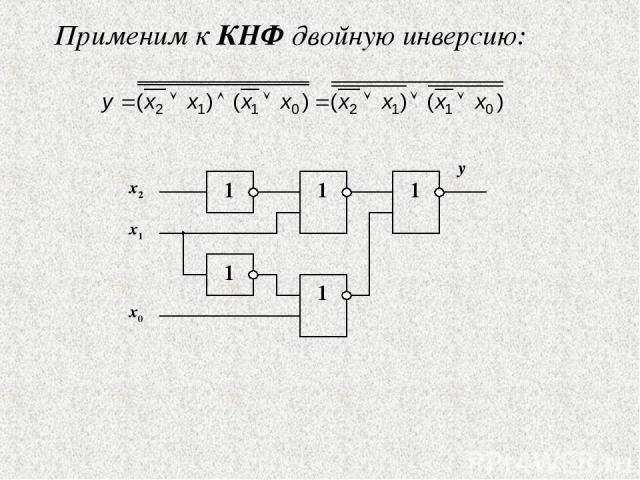
Применим к КНФ двойную инверсию:
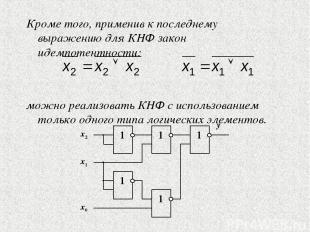
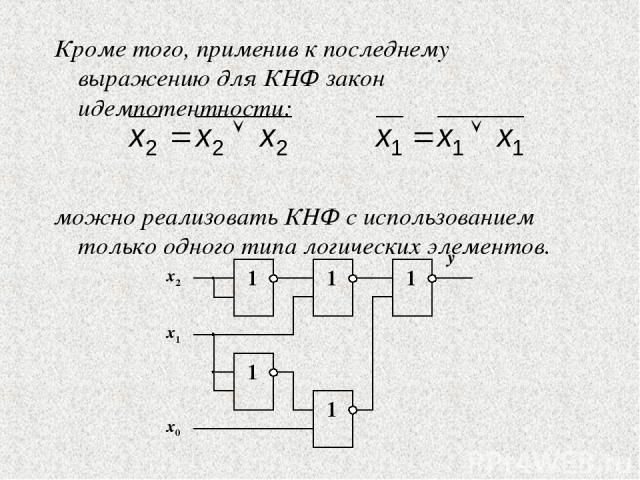
Кроме того, применив к последнему выражению для КНФ закон идемпотентности: можно реализовать КНФ с использованием только одного типа логических элементов.