Презентация на тему: Метод линейного программирования

Математические методы исследования операций глава 2. Линейное программирование Курс для студентов экономико-математических специальностей (часть 1)

Линейное программирование 1 Определение задачи ЛП КЗЛП и построение канонической формы Первая геометрическая интерпретация и графический метод решения Основные теоремы ЛП Вторая геометрическая интерпретация и базисные планы Теоремы о базисных планах

Линейное программирование 2 Симплекс-метод, алгоритм Модифицированный симплекс-метод Симплекс-метод, обоснование Проблема вырожденности Альтернативные оптимальные планы Метод минимизации невязок

Общая задача линейного программирования Общая задача линейного программирования (ОЗЛП)

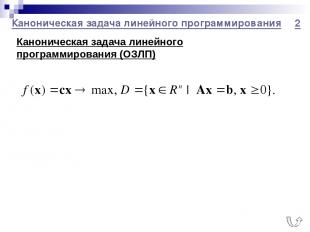
Каноническая задача линейного программирования 2 Каноническая задача линейного программирования (ОЗЛП)

Построение канонической формы 1

Построение канонической формы 2

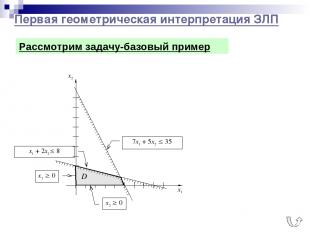
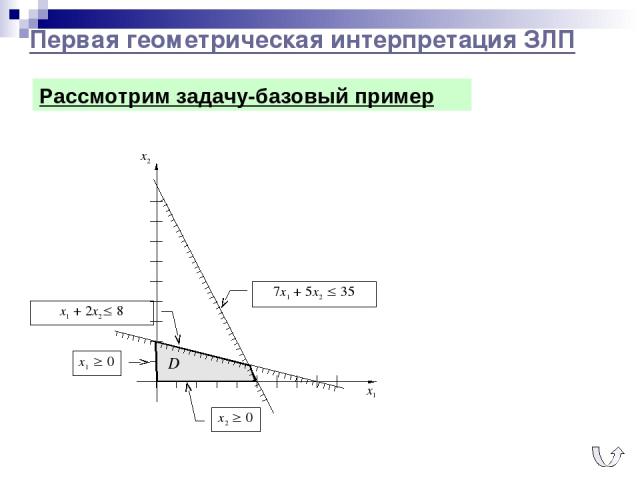
Первая геометрическая интерпретация ЗЛП x2   0 x1   0 Рассмотрим задачу-базовый пример

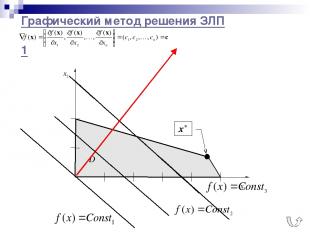
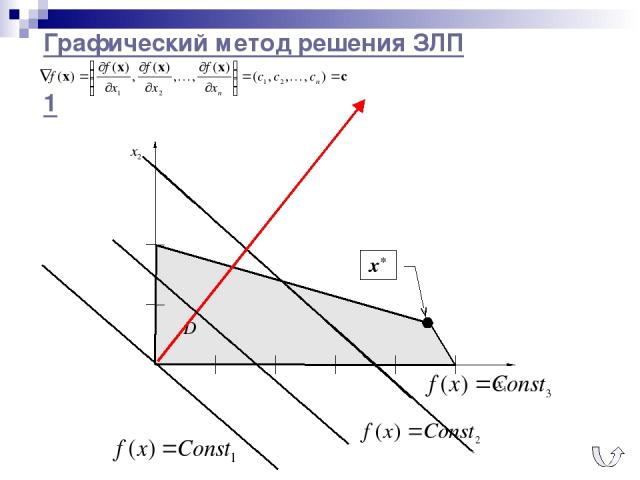
Графический метод решения ЗЛП 1

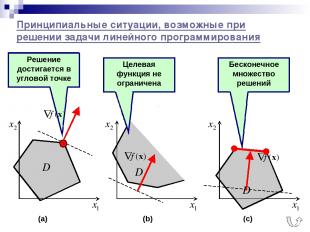
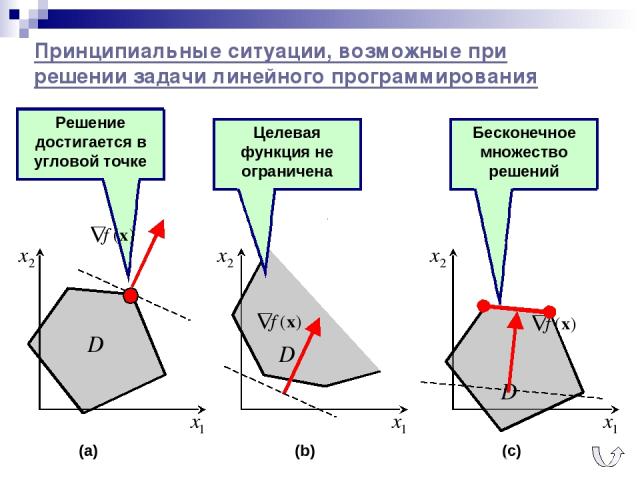
Решение достигается в угловой точке Принципиальные ситуации, возможные при решении задачи линейного программирования (a) (b) (c) Целевая функция не ограничена Бесконечное множество решений

Графический метод решения ЗЛП 2 Рассмотрим задачу

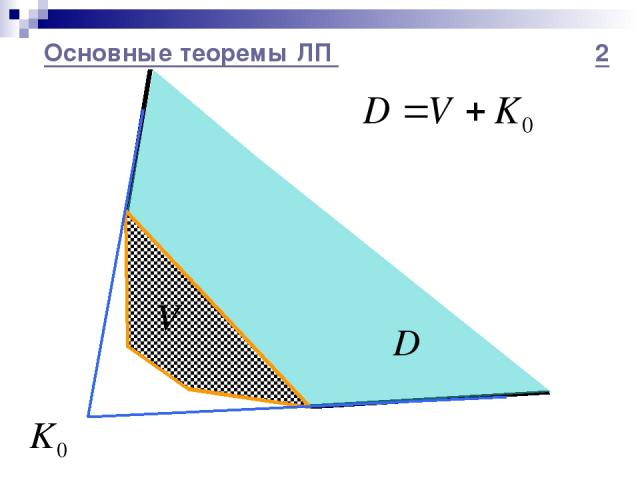
Основные теоремы ЛП 1 Теорема Доказательство Теорема о представлении многогранного выпуклого множества

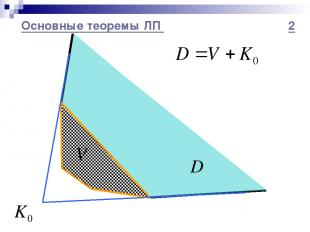
Основные теоремы ЛП 2

Основные теоремы ЛП 3 - угловые точки

Основные теоремы ЛП 4 - направляющие вектора конуса (!) рассуждения «от противного»

Основные теоремы ЛП 5 По свойства многогранного выпуклого конуса: (1)

Основные теоремы ЛП 5 (2) (3)

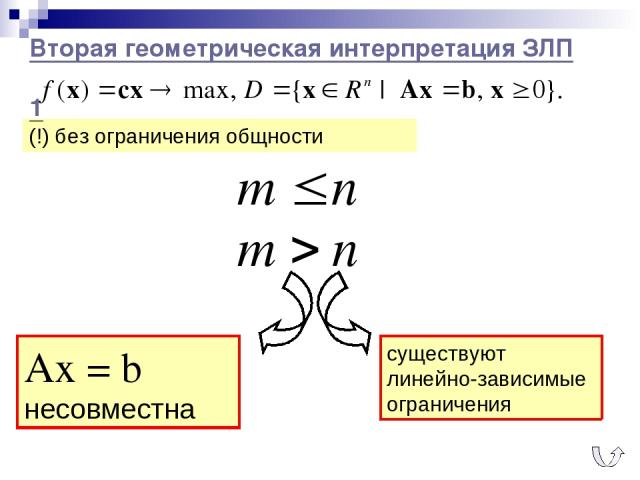
Вторая геометрическая интерпретация ЗЛП 1 (!) без ограничения общности Аx = b несовместна существуют линейно-зависимые ограничения

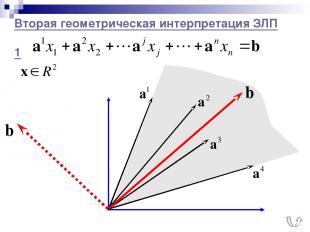
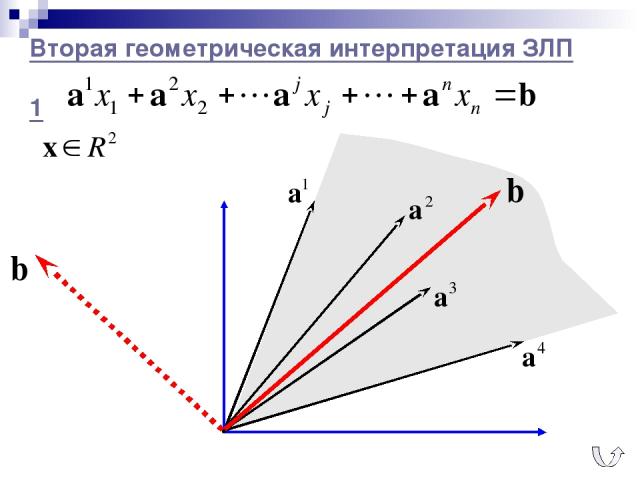
Вторая геометрическая интерпретация ЗЛП 1

Базисный план 1

Базисный план 2

Базисный план 3 базисный план-невырожденный: вырожденный – в противном случае.

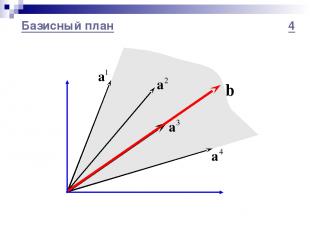
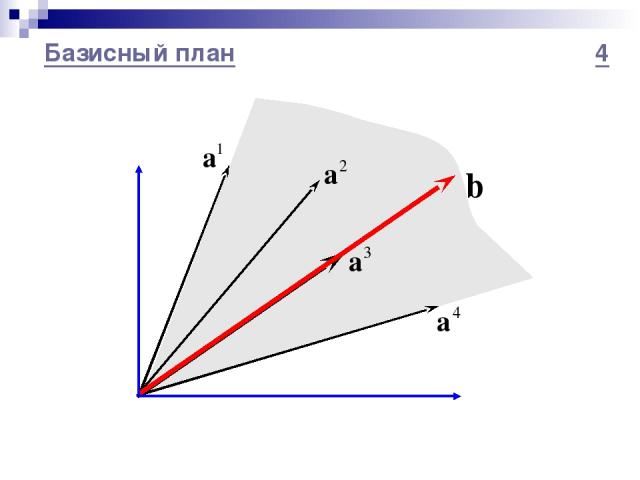
Базисный план 4

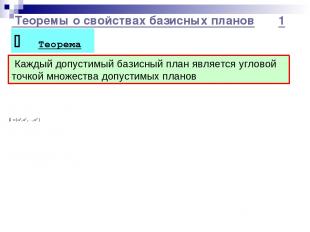
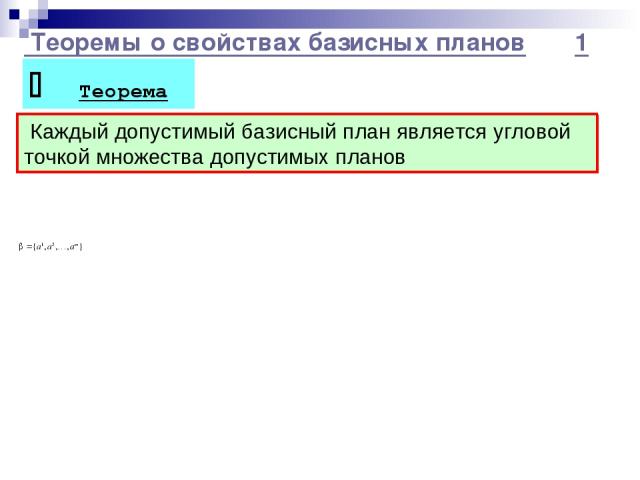
Теоремы о свойствах базисных планов 1 Теорема Каждый допустимый базисный план является угловой точкой множества допустимых планов

Теоремы о свойствах базисных планов 2

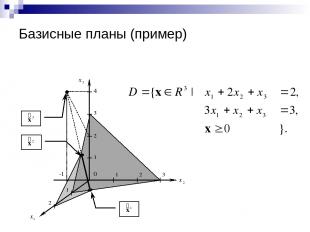
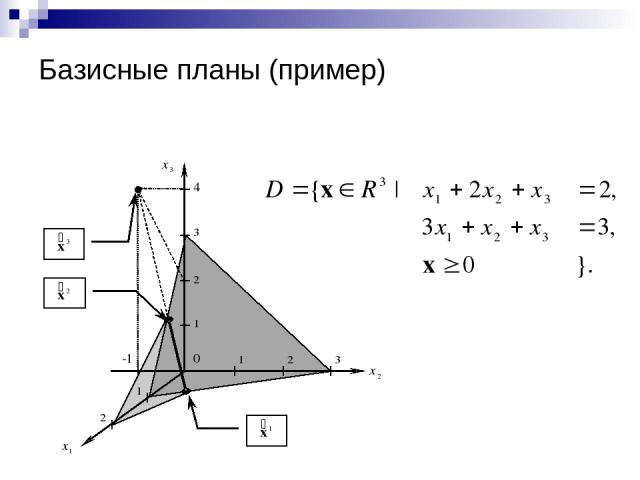
Базисные планы (пример)

Симплекс-метод, историческая справка Джордж Данциг (1914-2005), 1947 Леонид Витальевич Канторович (1912-1986), 1939

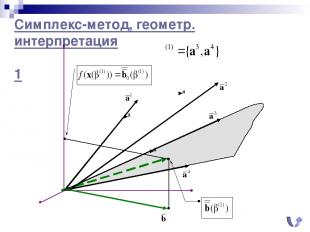
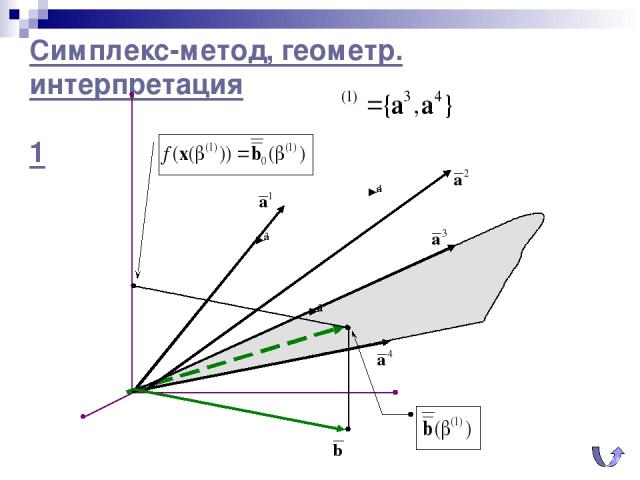
Симплекс-метод, геометр. интерпретация 1

Симплекс-метод, геометр. интерпретация 2

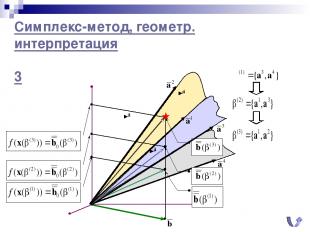
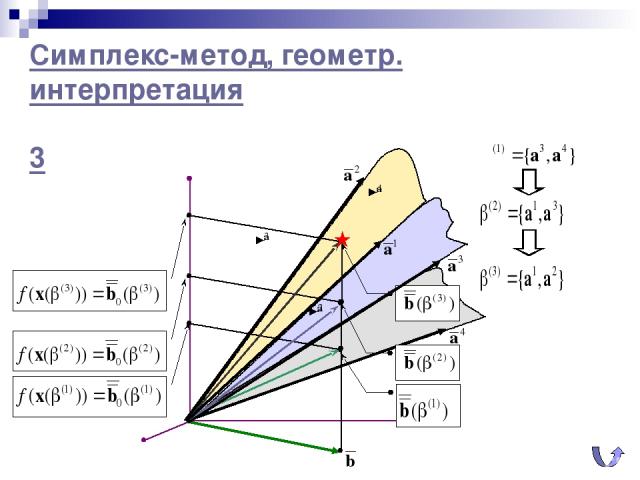
Симплекс-метод, геометр. интерпретация 3

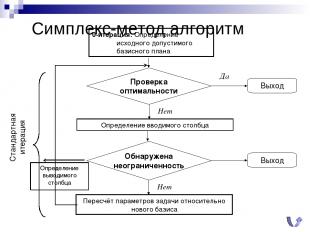
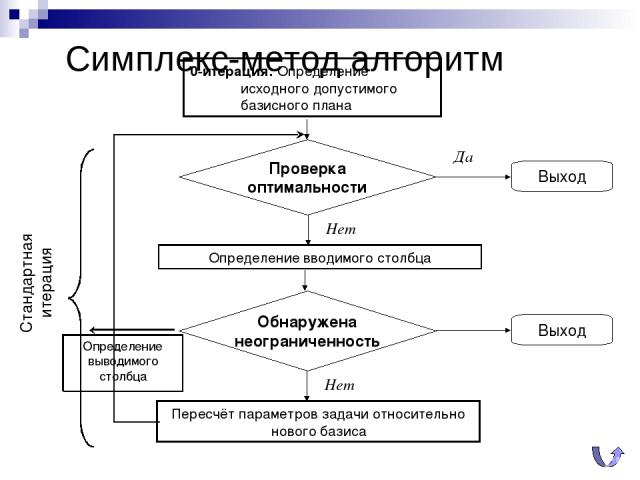
Симплекс-метод алгоритм 0-итерация: Определение исходного допустимого базисного плана Определение выводимого столбца

Симплекс-метод критерий оптимальности

Симплекс-метод определение выводимого столбца

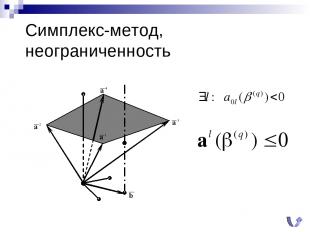
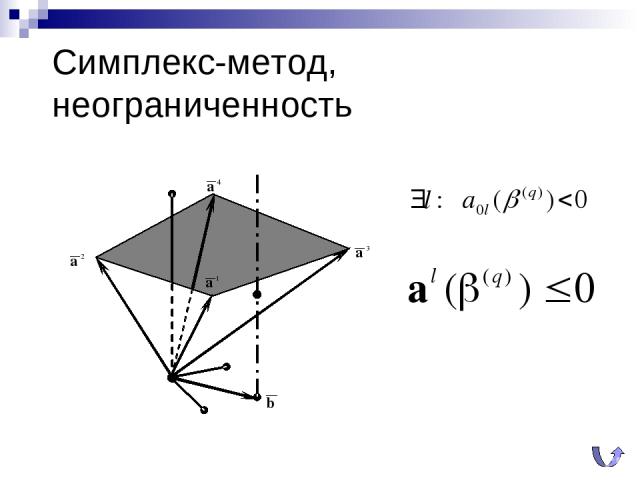
Симплекс-метод, неограниченность

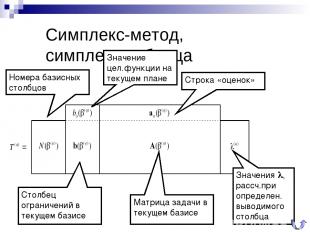
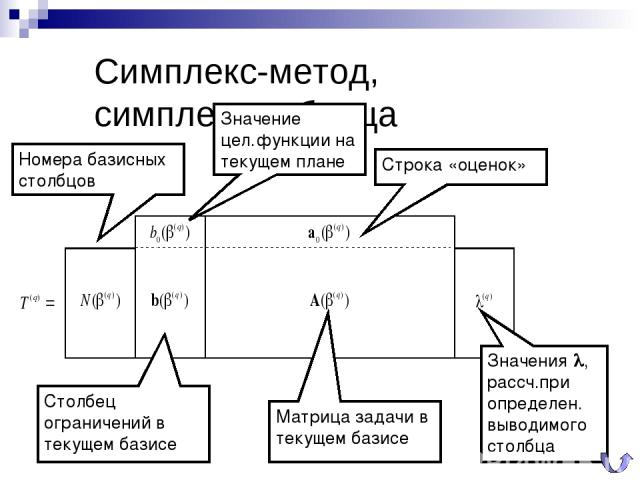
Симплекс-метод, симплекс-таблица Номера базисных столбцов Столбец ограничений в текущем базисе Матрица задачи в текущем базисе Строка «оценок» Значение цел.функции на текущем плане Значения l, рассч.при определен. выводимого столбца

Симплекс-метод, пример (0) Исходный допустимый базис

Симплекс-метод, пример (1)

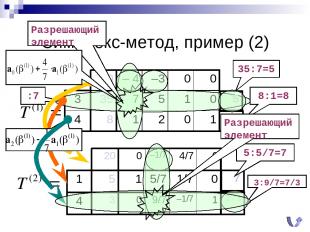
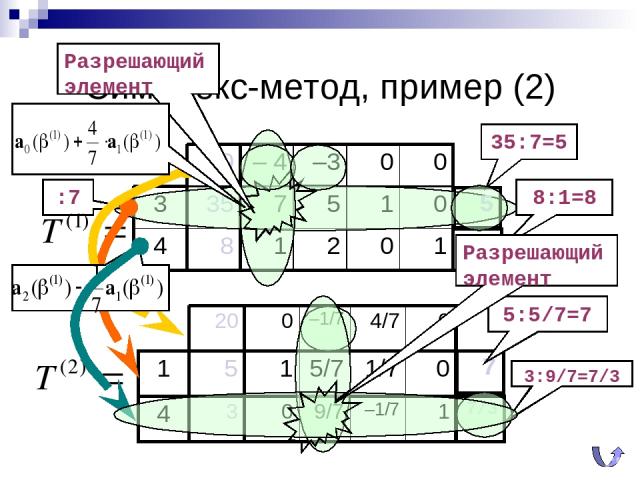
Симплекс-метод, пример (2) 35:7=5 8:1=8 Разрешающий элемент :7 5:5/7=7 3:9/7=7/3 Разрешающий элемент 4 3 0 9/7 –1/7 1 0 – 4 –3 0 0 3 35 7 5 1 0 4 8 1 2 0 1 5 8 1 5 1 5/7 1/7 0 20 0 –1/7 4/7 0 7 7/3

Симплекс-метод, пример (3) План оптимальный !!! 61/3 0 0 5/9 1/9 1 10/3 1 0 2/9 –5/9 2 7/3 0 1 –1/9 7/9

Симплекс-метод, метод минимизации невязок

Обоснование симплекс-метода Т1/1

Обоснование симплекс-метода Т1/2

Обоснование симплекс-метода Т2/1 (T2.1)

Обоснование симплекс-метода Т2/2 ? ?

Обоснование симплекс-метода Т2/3

Обоснование симплекс-метода Т3/1 (T3.1)

Обоснование симплекс-метода Т4/1

Сходимость симплекс-метода и проблема вырожденности 1 Рассмотрим пример

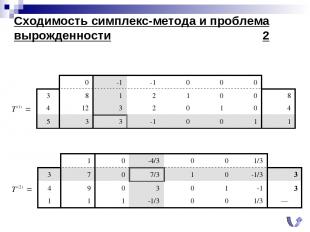
Сходимость симплекс-метода и проблема вырожденности 2

Сходимость симплекс-метода и проблема вырожденности 3

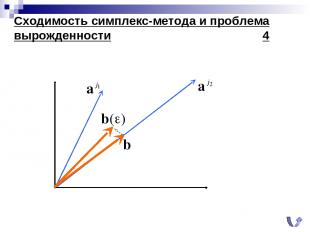
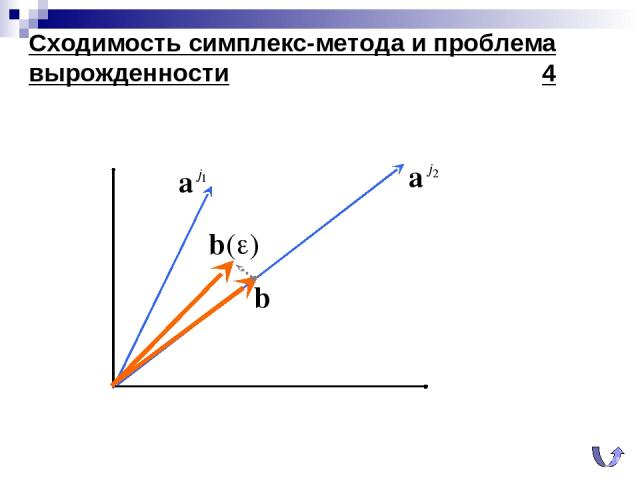
Сходимость симплекс-метода и проблема вырожденности 4

Сходимость симплекс-метода и проблема вырожденности 5 ( ) Базовая идея: переход к «возмущённой» задаче (В.1)

( ) Теорема Чарнса Сходимость симплекс-метода и проблема вырожденности 6

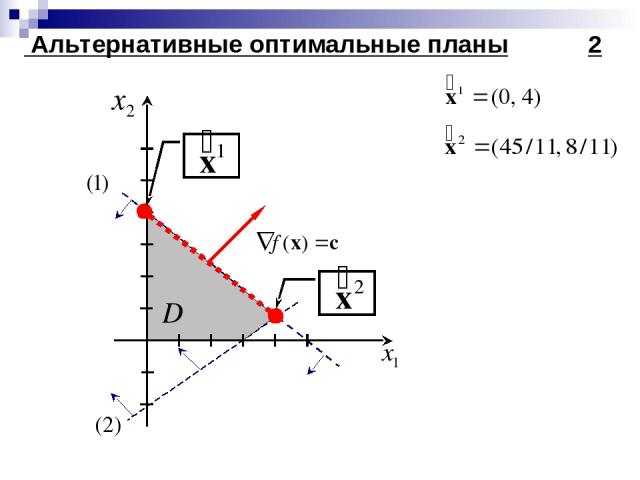
Альтернативные оптимальные планы 1 Рассмотрим пример

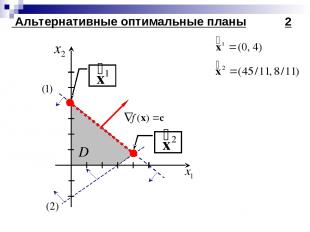
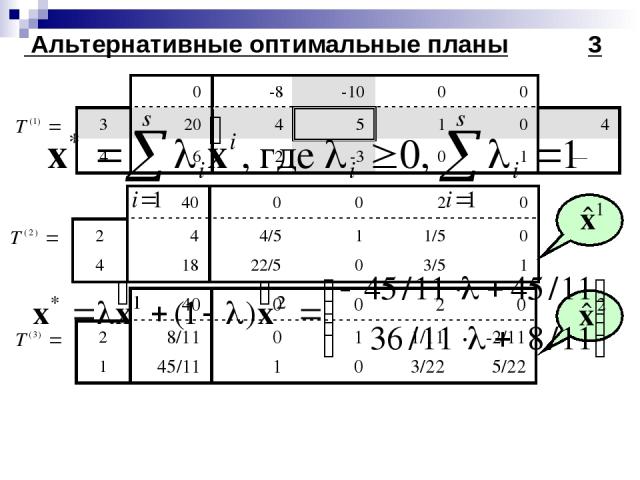
Альтернативные оптимальные планы 2

Альтернативные оптимальные планы 3

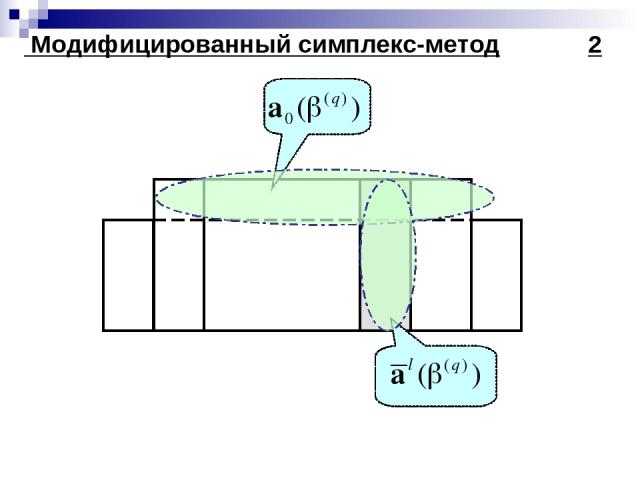
Модифицированный симплекс-метод 1

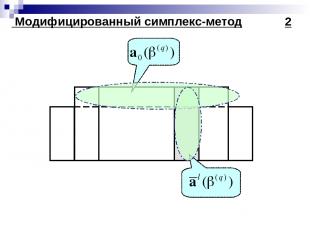
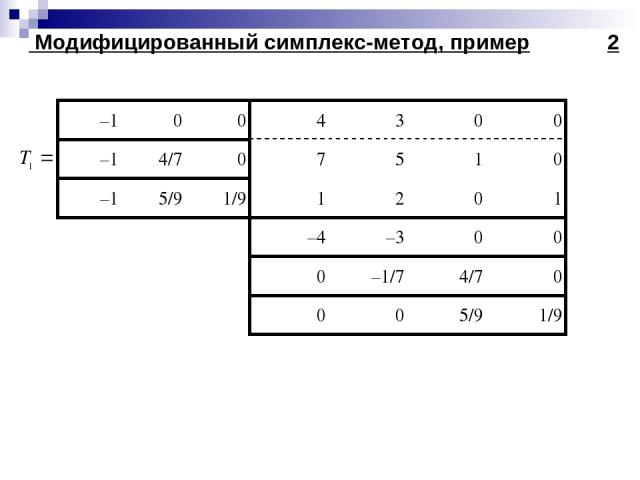
Модифицированный симплекс-метод 2

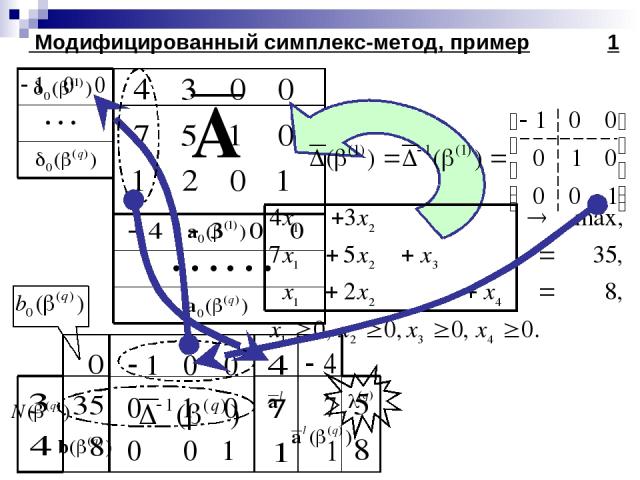
Модифицированный симплекс-метод, пример 1

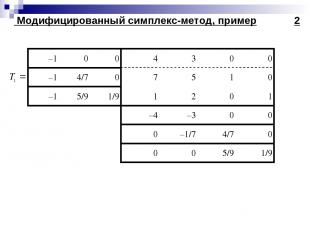
Модифицированный симплекс-метод, пример 2

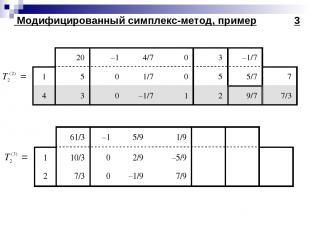
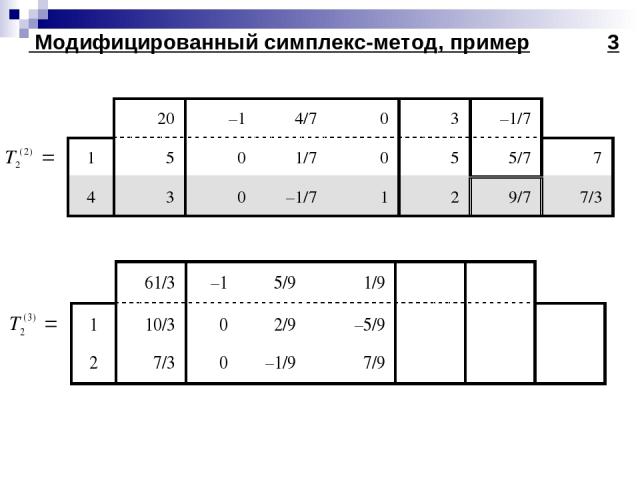
Модифицированный симплекс-метод, пример 3

Модифицированный симплекс-метод, мультипликативная форма 3 r-й столбец: Мультипликативная форма