Презентация на тему: Логические выражения

Логические основы построения компьютера. Выполнила :ученица 11 б класса Гинкель Регина Учитель: Скульбеда Н.И. МОУ «Новоархангельская СОШ» 900igr.net

Цель. 1. Познакомить учащихся с логическими основами компьютера. 2. Ввести понятия логических выражений. 3. Научить строить таблицы для логических функций.

Содержание. 1. Историческая справка. 2. Булева алгебра. 3Логические выражения. 3.1 Логическое отрицание. 3.2 Логическое сложение. 3.3 Логическое умножение. 3.4 Логическое следование. 3.5 Эквивалентность. 4.Построение таблиц. 5.Основные законы логики.

Историческая справка. Немецкий ученый Лейбниц первым (в 1666 году) попытался перевести законы мышления (формальную логику) из словесного царства, полного неопределенностей, в царство математики, где отношения между объектами или высказываниями определяются в виде математических соотношений. Спустя более ста лет, в 1816 году, уже после смерти Лейбница среди ученых шел разговор о создании логического универсального языка, подчиняющегося строгим математическим законам. В 1847 году Буль написал важную статью на тему «Математический анализ логики», а в 1854 году развил свои идеи в работе «Исследование законов мышления».

Буль изобрёл своеобразную алгебру – систему обозначений и правил, применимую ко всевозможным объектам, от чисел и букв до предложений. Его именем она теперь и называется: алгебра Буля, или булева алгебра.

Булева алгебра. Булева алгебра состоит из компонентов: Логические объекты ( выражения) Операции над логическими объектами Аксиомы и теоремы, регламентирующие эти операции

Логические выражения 1.Логические 2. Предикаты. утверждения

1. Логические утверждения – это конкретные частные утверждения, заведомо истинные или ложные, иначе говоря, это логические константы. Например: 2*2 = 4 ( истина) Волга впадает в Чёрное море. (ложь)

2. Предикаты – это логические высказывания, значения которых могут меняться в зависимости от входящих в них переменных величин, иначе говоря, это логические переменые. Например: А +В >С (принимают значения Истина или Ложь в зависимости от значений А, В, С)

Логическое отрицание. Логическое отрицание или Инверсия, определяется над одним аргументом (простым или сложным логическим выражением) следующим образом: если исходное выражение истинно, то результат его отрицания будет ложным, и наоборот. Операция означает, что к исходному логическому выражению добавляют частицу НЕ или слова НЕВЕРНО, ЧТО. Обозначается значком А ┐А 0 1 1 0

Логическое сложение. Логическое сложение или Дизъюнкция, определяет логическое соединение двух логических выражений (высказываний) с помощью союза ИЛИ. Обозначается значком Сложное логическое выражение будет истинным тогда и только тогда, когда истинно хотя бы одно из исходных (простых) логических выражений. ۷ ☺ запомни знак! Пример: для сдачи экзамена необходимы знания или везение. А В А۷В 0 0 0 0 1 1 1 0 1 1 1 1

Логическое умножение. Логическое умножение или Конъюнкция, определяет соединение двух логических выражений (высказываний) с помощью союза И. Обозначается значком & или ٨. Эта операция ставит в соответствие двум простым логическим выражениям новое- сложное, которое будет истинным тогда и только тогда, когда истинны оба исходных (простых) логических выражения. Запомни знак! Пример: Учитель должен быть умным и терпеливым (только одновременное наличие двух качеств, ума и терпения, делает выражение истинным). А В А٨В 0 0 0 0 1 0 1 0 0 1 1 1

Логическое следование. Логическое следование или Импликация. Эта операция связывает два простых логических выражения, из которых первое является условием, а второе- следствием из этого условия. Выражается словами ЕСЛИ…, ТО… Обозначается значком Результатом импликации является ложь тогда и только тогда, когда (А) истинно, а следствие (В) ложно. Например: Если выучишь материал, то сдашь зачет (высказывание ложно только тогда, когда материал выучен, а зачет не сдан, ведь сдать зачет можно и случайно, например если попался единственный знакомый вопрос или удалось воспользоваться шпаргалкой. А В А В 0 0 1 0 1 1 1 0 0 1 1 1

Эквивалентность. Эквивалентность или Равнозначность. Определяет результат сравнения двух простых логических выражений А и В, обозначается значком Результат – новое логическое выражение, которое является истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны. Пример: Когда в зимний день светит солнце и «кусает» мороз, это значит, что атмосферное давление высокое. А В А В 0 0 1 0 1 0 1 0 0 1 1 1

Порядок выполнения логических операций. 1. Инверсия - ┐ 2. Конъюнкция - & или ٨ 3. Дизъюнкция – ۷ 4. Импликация – 5. Эквивалентность - Для изменения указанного порядка выполнения логических операций используются круглые скобки. Например: D = ┐( A ۷ B ٨ C)

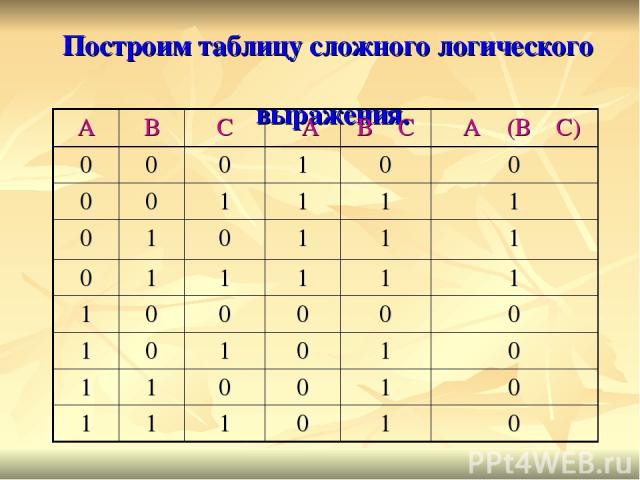
Построение таблиц. Рассмотрим пример построения таблицы истинности для следующегося сложного (составного) логического выражения. D = ┐A ٨ (B ۷ C) Сначала нужно установить число строк и столбцов такой таблицы, то есть спланировать форму таблицы. При определении числа строк необходимо некоторым образом перебрать все возможные сочетания логических значений 0 и 1 исходных выражений А, В и С, из которых формируется заданное сложное логическое выражение.

При добавлении третьего аргумента сначала запишем первые 4 строки таблицы, сочетания их со значением третьего аргумента, равным 0, а затем ещё раз запишем эти же 4 строки, но теперь уже со значением третьего аргумента, равным 1. В результате в таблице для трех аргументов окажется 8 строк (+ девятая строка – шапка таблицы), и при таком подходе легко проверить, что мы действительно не повторили и не пропустили ни одного возможного сочетания логических значений аргументов – исходных выражений А, В, С

Существует закономерность: для любого числа N аргументов сложного логического выражения таблица истинности содержит 2n строк, а также строку заголовка (шапка таблицы). Количество столбцов таблицы истинности для её построения выбирают равным М. Эти столбцы соответствуют значениям исходных выражений А, В, С, промежуточных результатов ┐А, (В ۷ С), а также искомого окончательного результата- значения сложного арифметического выражения ┐А ٨ (В ۷ С)

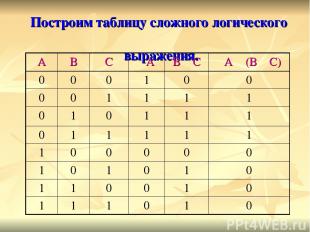
Построим таблицу сложного логического выражения. А В С ┐А В ۷ С ┐А ٨ (В ۷ С) 0 0 0 1 0 0 0 0 1 1 1 1 0 1 0 1 1 1 0 1 1 1 1 1 1 0 0 0 0 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 1 0

Основные законы логики. 1.Отсутствие степеней и коэффициентов (идемпотентность): А ٨ А= А; А ۷ А= А 2.Двойное отрицание (инволюция): ¬(¬А) = А 3.Закон исключения третьего: А۷¬ А=1(всегда истина) 4.Закон противоречия: А ٨ ¬ А= 0 (всегда ложь) 5.Независимость от перестановки мест (коммутативность): А۷ В= В ۷ А; А ٨ В = В ٨ А 6. Независимость от порядка выполнения однотипных действий (ассоциативность): (А۷В) ۷ С = А ۷ (В۷С); (А٨В) ٨ С = А ٨ (В٨С).

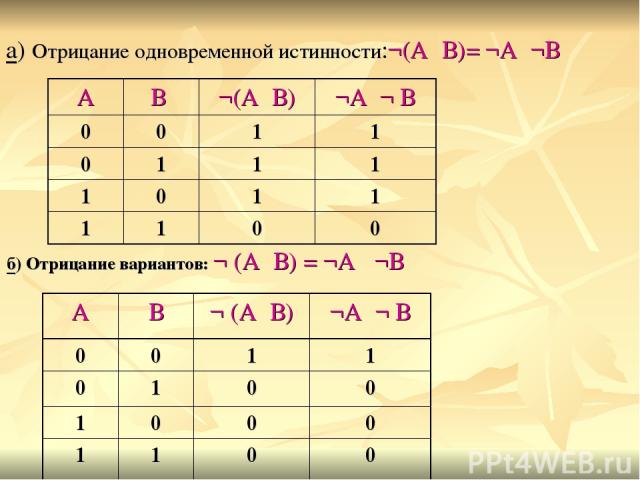
7. Дистрибутивность (распределение): Умножения- (А۷В) ٨ С = (А٨С) ۷ (В٨С) и наоборот: (А٨В) ۷ (В٨С) = В ٨ (А۷С). Сложения- А۷В٨С = (А۷В) ٨ (А۷С). 8. Законы де Моргана: а) Отрицание одновременной истинности:¬(А٨В)= ¬А۷¬В б) Отрицание вариантов: ¬ (А۷В) = ¬А ٨¬В

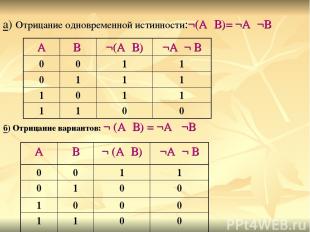
б) Отрицание вариантов: ¬ (А۷В) = ¬А ٨¬В а) Отрицание одновременной истинности:¬(А٨В)= ¬А۷¬В А В ¬ (А۷В) ¬А٨¬ В 0 0 1 1 0 1 0 0 1 0 0 0 1 1 0 0 А В ¬(А٨В) ¬А۷¬ В 0 0 1 1 0 1 1 1 1 0 1 1 1 1 0 0

Используемая литература. 1.Макарова Н.В. /методическое пособие для учителей. 2.Макарова Н.В. /практикум по информационным технологиям.