Презентация на тему: Дерево. Следующие вершины, листья. Предыдущие вершины

Презентацию составила: учитель информатики Фефелова Любовь Степановна МОУ Большееланской СОШ Усольского района Иркутской области Урок 8 3 класс

Сформировать понятие «дерево»; Научить строить дерево, определять корневые вершины и листья; воспитывать самостоятельность; Развивать познавательную способность учащихся.

Личностные: развитие мотивов учебной деятельности; развитие самостоятельности и личной ответственности за свои поступки; развитие навыков сотрудничества

Метапредметные: освоение способов решения проблем творческого характера; формирование умения планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями её реализации; использование знаково-символических средств представления информации для создания моделей изучаемых объектов и процессов, схем решения учебных и практических задач.

Предметные: цепочка (конечная последовательность); дерево, понятия, связанные со структурой дерева; игра с полной информацией для двух игроков, понятия: правила игры, ход игры, позиция игры, выигрышная стратегия; выделение, построение и достраивание по системе условий: цепочки, дерева, мешка; определение значения истинности утверждений для данного объекта; понимание описания объекта с помощью истинных и ложных утверждений, в том числе включающих понятия: все/каждый, есть / нет, всего, не; использование имен для указания нужных объектов.

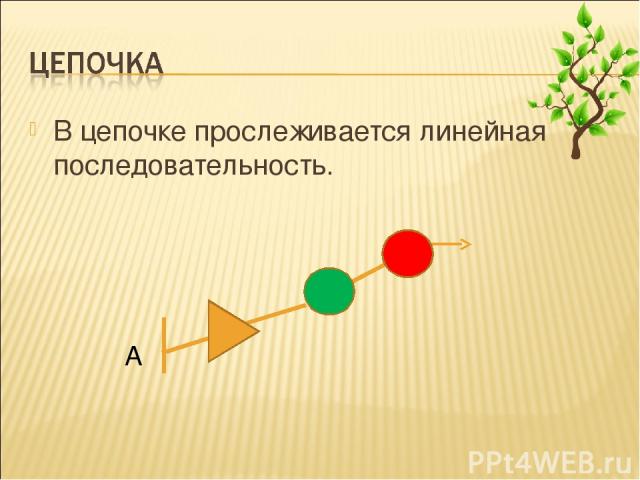
В цепочке прослеживается линейная последовательность.

Например: Из какой это сказки отрывок? "На развилине путей-дорог лежит Вещий камень, а на нём надпись: «Направо пойдёшь – коня потеряешь, себя спасёшь; налево пойдёшь – себя потеряешь, коня спасёшь; прямо пойдёшь – и себя и коня потеряешь»

2. Мы выбираем один из возможных объектов, но хотим потом изменить своё решение и выбрать другой. 3. Мы выделяем в задаче подзадачи, раздаём их участникам проекта, а потом собираем результаты для поиска одного решения.

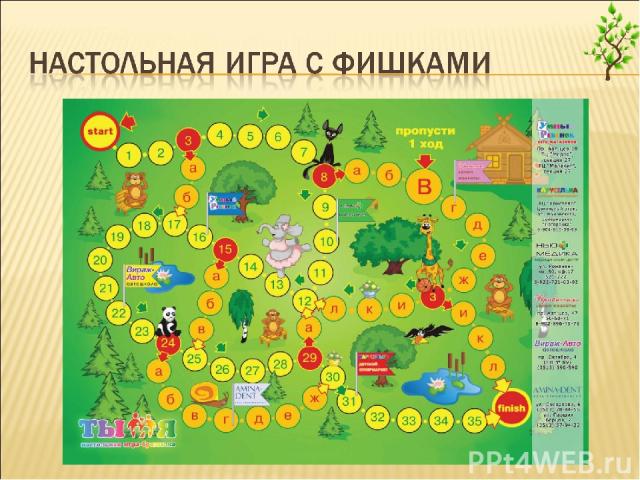
Во всех этих случаях одним выбором дело не заканчивается — ситуация выбора, ветвления может повторяться. Например, игроки в процессе игры делают выбор много раз — почти при каждом своём ходе. При попытке изобразить эту ситуацию на бумаге возникают графические схемы, называемые деревьями.

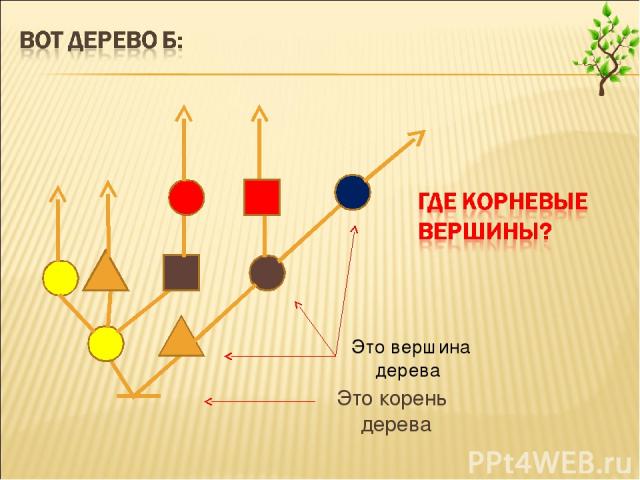
вершины, следующие после корня дерева, называются корневыми вершинами, корневых вершин в дереве может быть несколько; деревья направлены, они «растут» в одну сторону: у каждой вершины, если она не является листом, может быть несколько следующих вершин и ровно одна предыдущая, если вершина не корневая (у корневой вершины нет предыдущей).

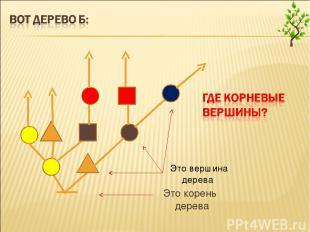
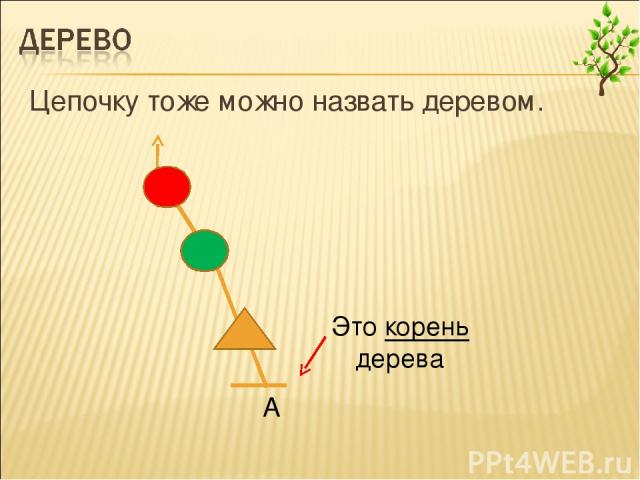
Это корень дерева Это вершина дерева

в каждой вершине дерева обязательно находится некоторый объект — буква, цифра, бусина, фигурка (вообще, бывают и такие деревья, не все вершины которых помечены, т. е. не в каждой вершине стоит какой-то объект).

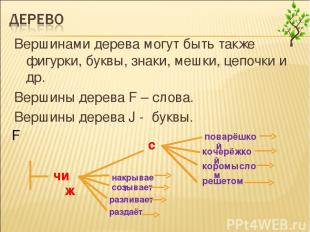
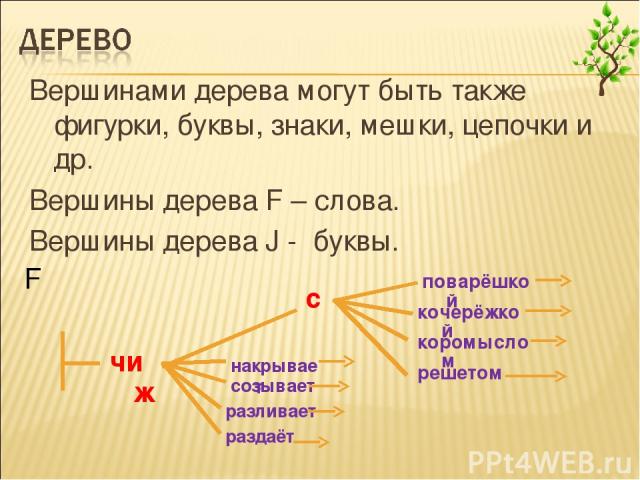
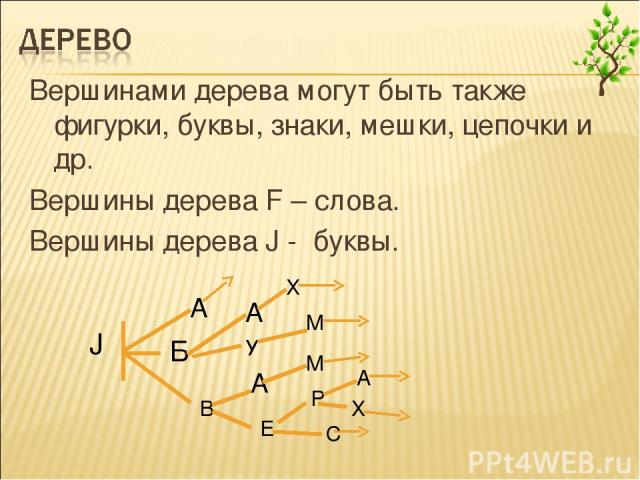
Вершинами дерева могут быть также фигурки, буквы, знаки, мешки, цепочки и др. Вершины дерева F – слова. Вершины дерева J - буквы. F

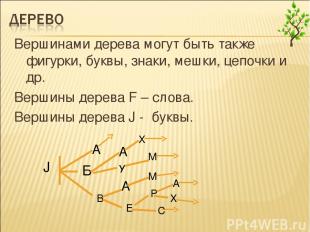
Вершинами дерева могут быть также фигурки, буквы, знаки, мешки, цепочки и др. Вершины дерева F – слова. Вершины дерева J - буквы. J

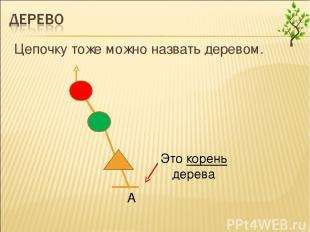
Цепочку тоже можно назвать деревом.

Вот утверждения, истинные для дерева D: У цифры 5 ровно одна следующая вершина. У цифры 8 нет следующих вершин. Следующие вершины цифры 7 – это цифры 8 и 6. 7

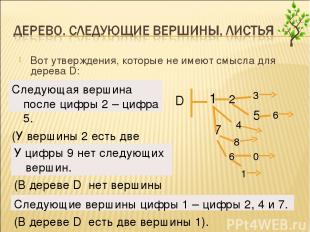
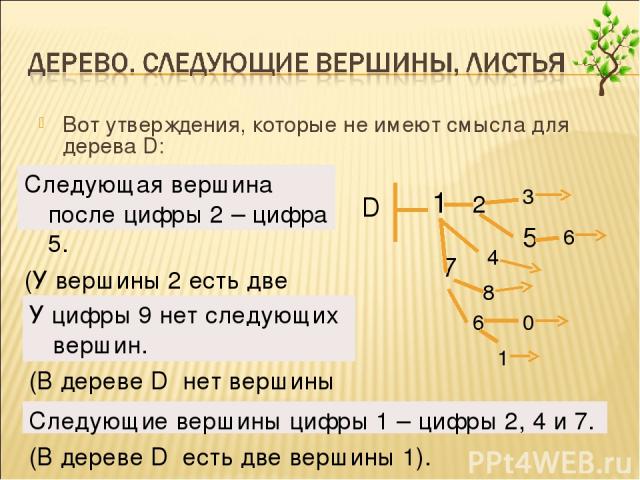
Вот утверждения, которые не имеют смысла для дерева D: Следующая вершина после цифры 2 – цифра 5. (У вершины 2 есть две следующие вершины) У цифры 9 нет следующих вершин. (В дереве D нет вершины 9). Следующие вершины цифры 1 – цифры 2, 4 и 7. (В дереве D есть две вершины 1). 7

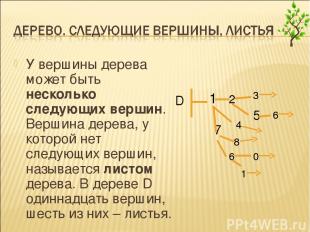
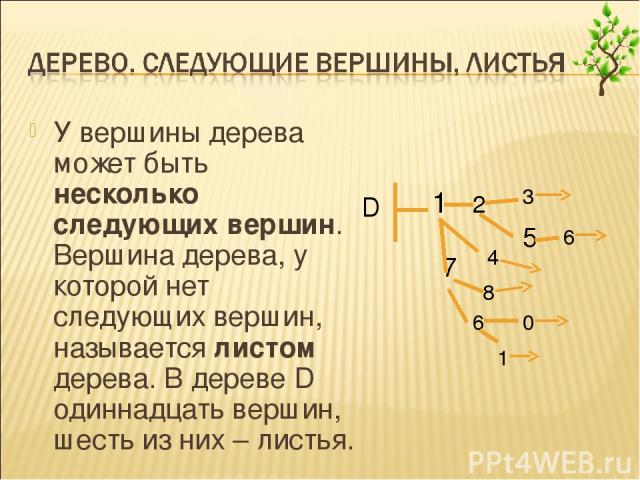
У вершины дерева может быть несколько следующих вершин. Вершина дерева, у которой нет следующих вершин, называется листом дерева. В дереве D одиннадцать вершин, шесть из них – листья.

Раскрась все бусины в дереве Ч какими хочешь цветами. Затем нарисуй в окне мешок всех листьев дерева Ч.

Ответ: «Ни у одной вершины дерева нет следующих вершин». При правильном построении дерева данное утверждение должно быть истинным. Задача 28.

Задача 29. Ответ: ложные утверждения для дерева У: Утверждение В (предыдущая фигурка перед дельфином — белка). Утверждение С (у жирафа три следующие фигурки — лев, лось и курица). Утверждение Н (фигурка верблюда в дереве есть). Утверждение G (у бегемота две следующие фигурки — волк и гусь). Утверждение К (предыдущая фигурка перед курицей — жираф). Остальные утверждения истинны.

Ответить на вопрос (обсуждение классом): Почему каждый объект является или не является деревом? Ответ: например: F не является деревом, поскольку у синей квадратной бусины две предыдущих. Это же условие нарушено и в схемах J и V. Оставшиеся две схемы являются деревьями.

Ответ: КАША КИЛЬКА КОМОД КОТИК КРЕСТ КРУЖКА КТО КТО-ТО КУСТ Задача на расстановку слов в словарном порядке.

Задание. Нарисуй дерево F и J. Определи: сколько корневых вершин и листьев в этих деревьях? Запиши ответ по форме: 1.В дереве F: корневых вершин- листьев – 2. В дереве J: корневых вершин – листьев -

Выполнить задание 32, 33.

Семенов А.Л., Рудченко Т.А. Информатика. 3 класс. Учебник для общеобразовательных учреждений. Часть 1. 3-е издание. – Москва «Просвещение», Институт новых технологий, 2011. – 104 с.; Семенов А.Л., Рудченко Т.А. Информатика. Рабочая тетрадь. 3 класс. Часть 1. Пособие для учащихся общеобразовательных учреждений. 2-е издание, доработанное. – Москва «Просвещение», Институт новых технологий, 2010. – 48 с.; Семенов А.Л., Рудченко Т.А. Информатика. Тетрадь проектов. 3 класс. Часть 1. Пособие для учащихся общеобразовательных учреждений. 2-е издание. – Москва «Просвещение», Институт новых технологий, 2010. – 12 с.; Семенов А.Л., Рудченко Т.А. Информатика. Книга для учителя. 3 класс – Москва «Просвещение», Институт новых технологий, 2009.