Презентация на тему: Свойства функции y=sin(x) и ее график

* y x 2π π - π - 2π 0 Автор Попова Л.А.

Свойства функции 1.D(y) 2.E(y) 3. Четность функции 4. Периодичность функции 5.Нули функции 6. Наибольшее значение 7. Наименьшее значение 8. Положительные значения 9. Отрицательные значения 10. Возрастание функции 11. Убывание функции *

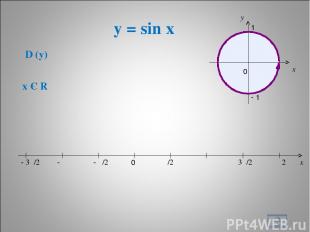
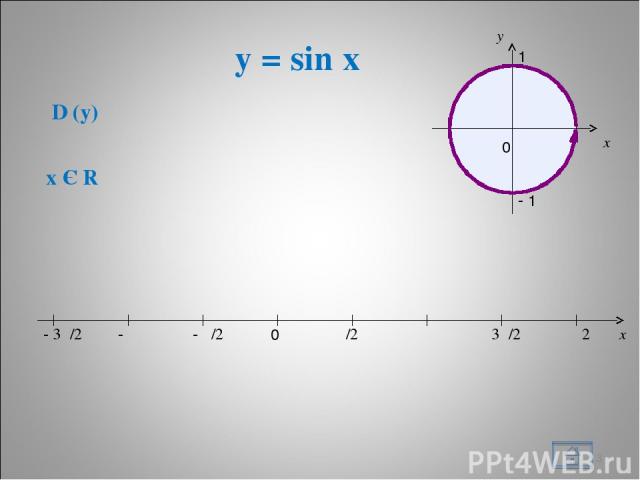
y = sin x * x 0 π/2 π 3π/2 2π - π/2 - π - 3π/2 D (y) x Є R

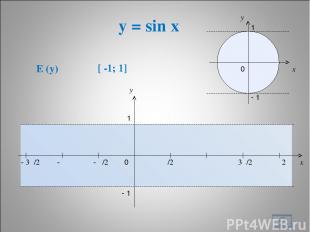
y = sin x * x y 0 π/2 π 3π/2 2π x y 1 - 1 - π/2 - π - 3π/2 1 - 1 0 E (y) [ -1; 1]

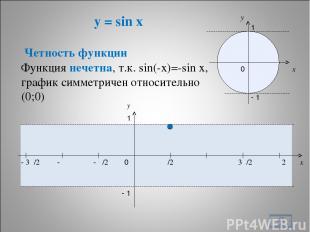
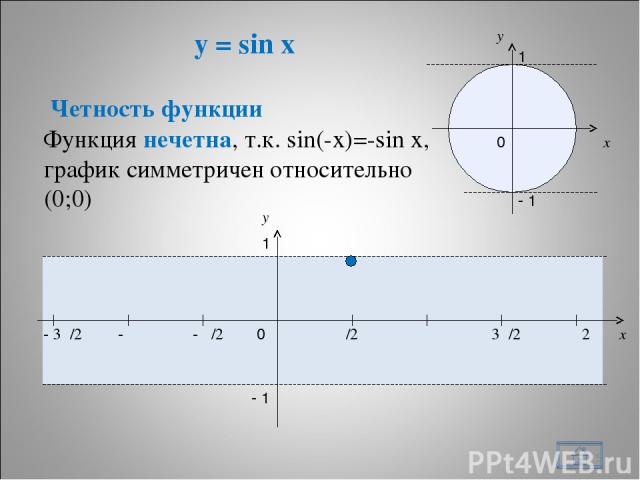
y = sin x * x y 0 π/2 π 3π/2 2π x y 1 - 1 - π/2 - π - 3π/2 1 - 1 0 Четность функции Функция нечетна, т.к. sin(-x)=-sin x, график симметричен относительно (0;0)

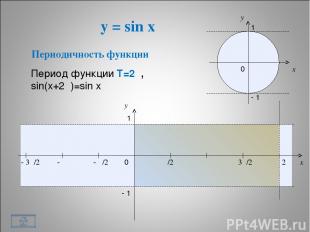
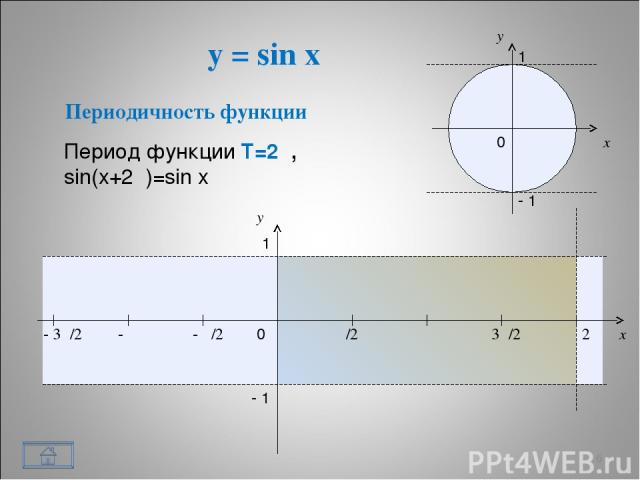
y = sin x * x y 0 π/2 π 3π/2 2π x y 1 - 1 - π/2 - π - 3π/2 1 - 1 0 Периодичность функции Период функции Т=2π, sin(x+2π)=sin x

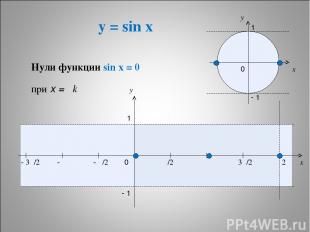
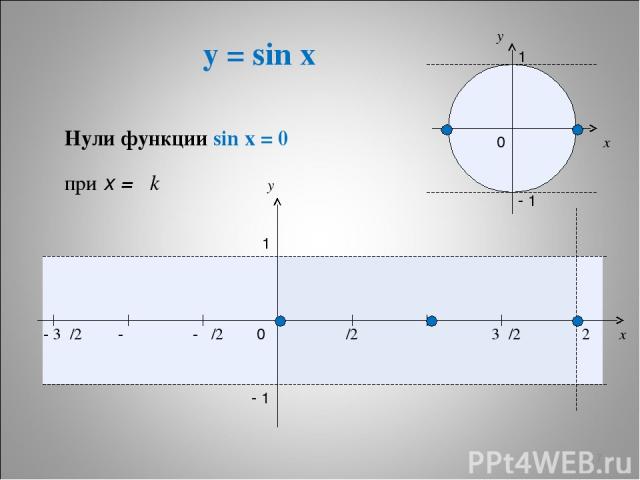
y = sin x * x y 0 π/2 π 3π/2 2π x y 1 - 1 - π/2 - π - 3π/2 1 - 1 0 Нули функции sin x = 0 при x = πk

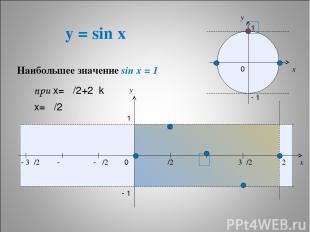
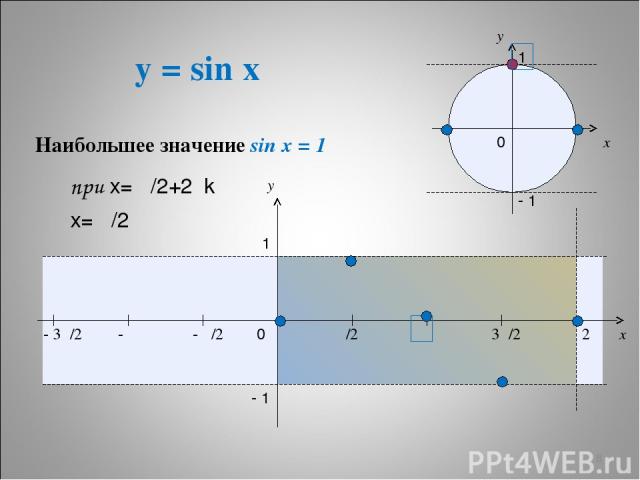
y = sin x * x y 0 π/2 π 3π/2 2π x y 1 - 1 - π/2 - π - 3π/2 1 - 1 0 Наибольшее значение sin x = 1 при х= π/2+2πk х= π/2

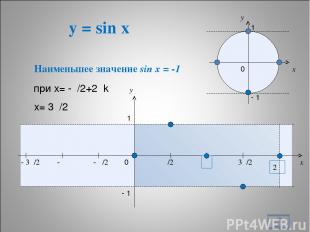
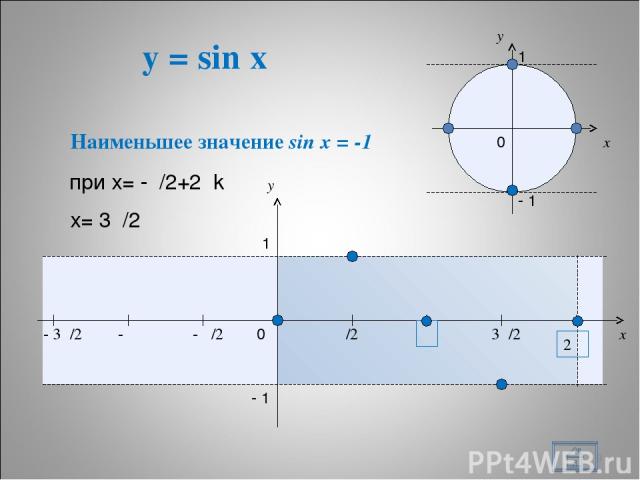
y = sin x * x y 0 π/2 π 3π/2 2π x y 1 - 1 - π/2 - π - 3π/2 1 - 1 0 Наименьшее значение sin x = -1 при х= -π/2+2πk х= 3π/2

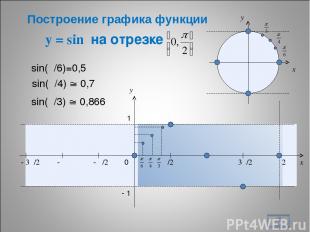
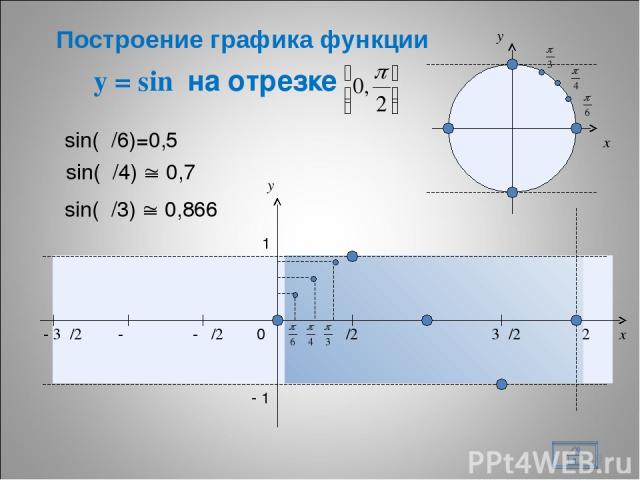
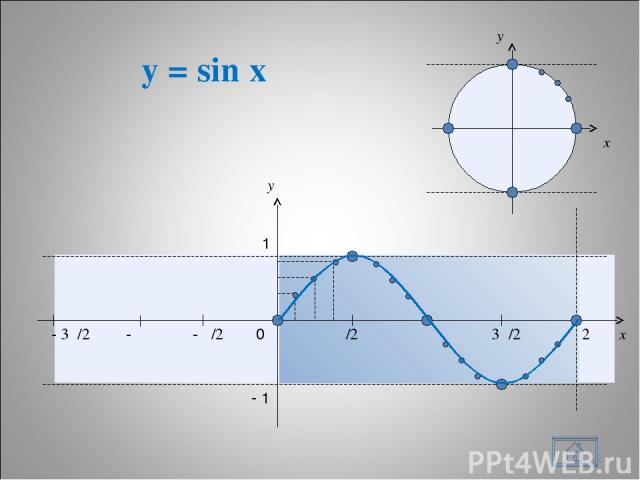
y = sin на отрезке * x y 0 π/2 π 3π/2 2π x y 1 - 1 - π/2 - π - 3π/2 sin(π/6)=0,5 sin(π/4) 0,7 sin(π/3) 0,866 Построение графика функции

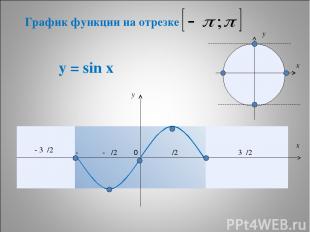
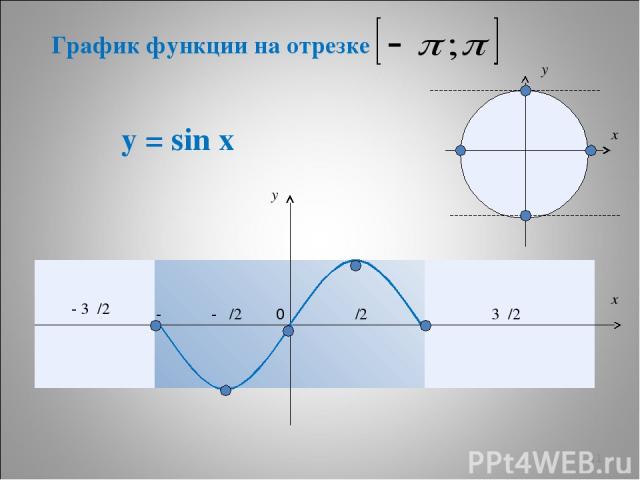
* у = sin x π π/2 - π/2 - π - 3π/2 3π/2 y x 0 y x График функции на отрезке

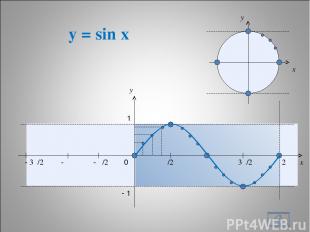
y = sin x * x y 0 π/2 π 3π/2 2π x y 1 - 1 - π/2 - π - 3π/2

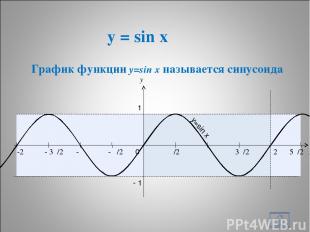
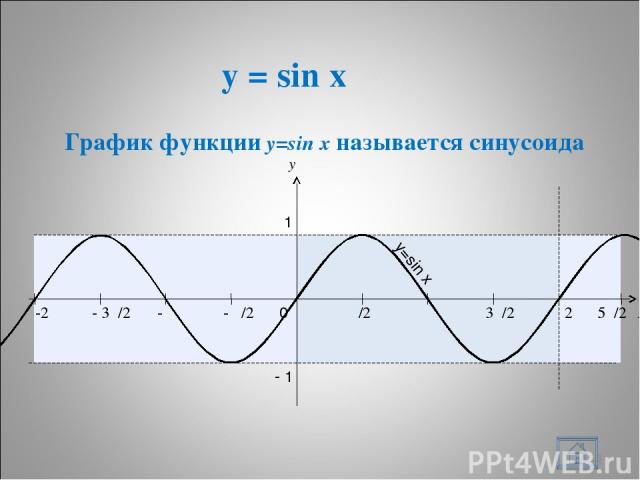
y = sin x * x y 0 π/2 π 3π/2 2π 1 - 1 - π/2 - π - 3π/2 -2π 5π/2 y=sin x График функции y=sin x называется синусоида

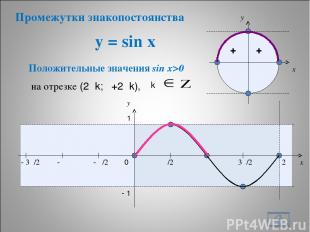
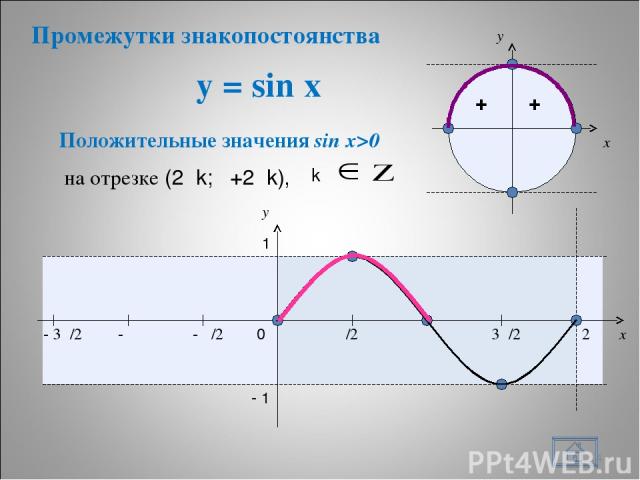
y = sin x * + + x y 0 π/2 π 3π/2 2π x y 1 - 1 Положительные значения sin x>0 - π/2 - π - 3π/2 на отрезке (2πk; π+2πk), Промежутки знакопостоянства k k

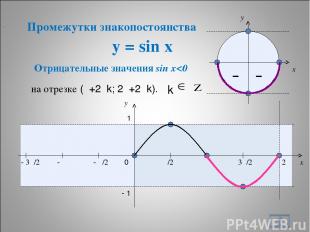
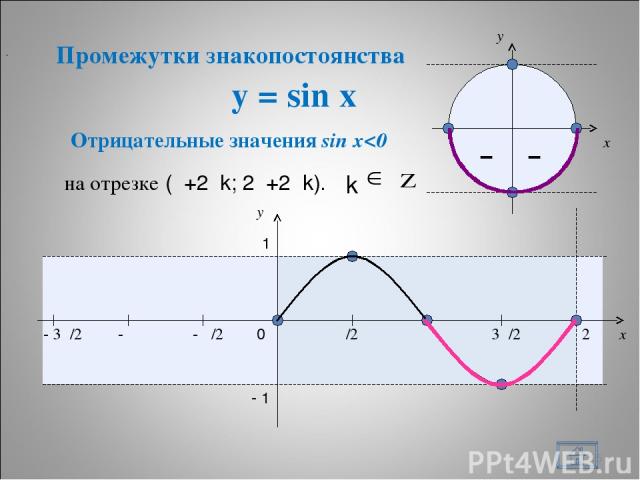
y = sin x * – – x y 0 π/2 π 3π/2 2π x y 1 - 1 Отрицательные значения sin x

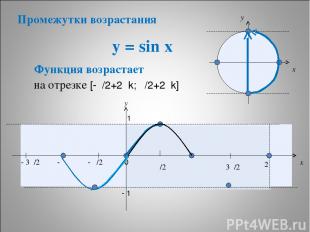
y = sin x * x y 0 π/2 π 3π/2 2π x y 1 - 1 Функция возрастает - π/2 - π - 3π/2 на отрезке [-π/2+2πk; π/2+2πk] Промежутки возрастания

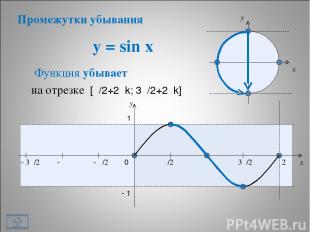
y = sin x * x y 0 π/2 π 3π/2 2π x y 1 - 1 Функция убывает - π/2 - π - 3π/2 на отрезке [π/2+2πk; 3π/2+2πk] Промежутки убывания

* Сравнить числа sin 2 и sin 3 Задача Так как = 3,14, , то < 2 < 3 < Из графика видно, что на отрезке функция у=sinх убывает. Ответ: sin 2 > sin 3.

Упражнения Пользуясь свойствами функции у = sin x , сравните числа: sin 1000 и sin 1300 sin 4 и sin 2 и

Расположить в порядке возрастания числа sin 1.9 ; sin 3; sin(-1); sin(-1.5). Числа sin 1.9 и sin 3 положительны, так как точки Р1,9 и Р3 находятся во 2 четверти. Функция у=sinх во 2 четверти убывает. sin 3 < sin 1.9 Числа sin(-1) и sin(-1.5) отрицательны, так как точка Р(-1) и Р(-1,5) находятся в 4 четверти. Функция у=sinх во 4 четверти возрастает.. sin(-1.5) < sin(-1.5) Ответ: Таким образом, в порядке возрастания эти чила располагаются так: sin(-1.5); sin(-1); sin 3; sin 1.9.

Используя свойство возрастания или убывания функции y=sinx, сравните числа: и и и и 1 вариант 2 вариант

* Разбить отрезок на два так, чтобы на одном из них функция у=sin х убывала, а на другом возрастала. Ответ; На отрезке функция у=sin х убывает, а на отрезке функция возрастает.

№ 722 Разбить данный отрезок на два отрезка так, чтобы на одном из них функция у=sinх возрастала, а на другом убывала. 1) - Функция возрастает - Функция убывает 2) - Функция убывает - Функция возрастает 3) - Функция убывает - Функция возрастает

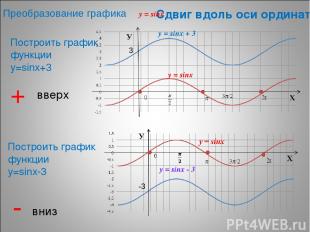
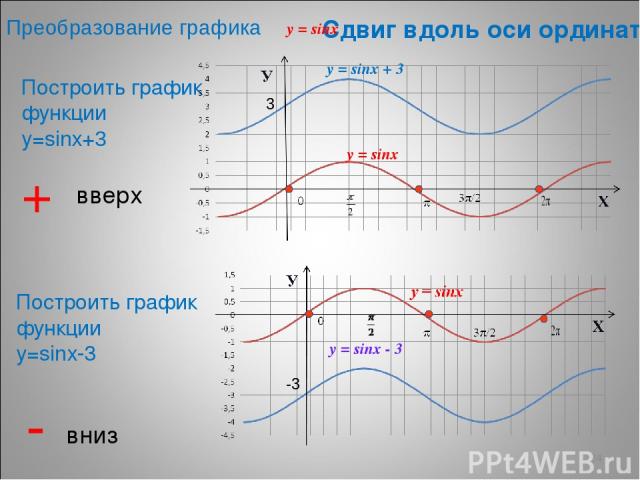
* Сдвиг вдоль оси ординат Построить график функции у=sinх+3 Построить график функции у=sinх-3 + вверх - вниз y = sinx y = sinx + 3 y = sinx y = sinx - 3 3 -3 Преобразование графика

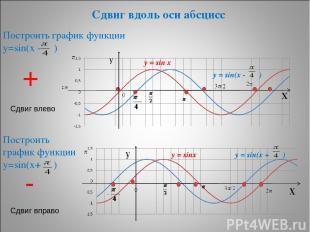
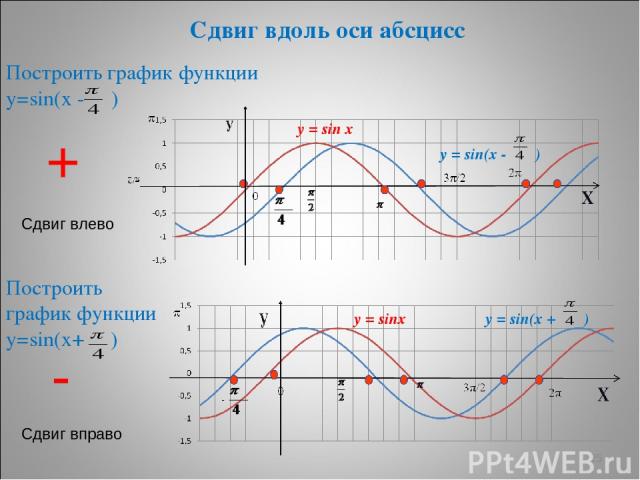
* Сдвиг вдоль оси абсцисс Построить график функции у=sin(х - ) Построить график функции у=sin(х+ ) + Сдвиг влево - Сдвиг вправо y = sin x y = sin(x - ) y = sin(x + ) y = sinx

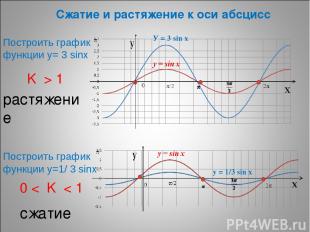
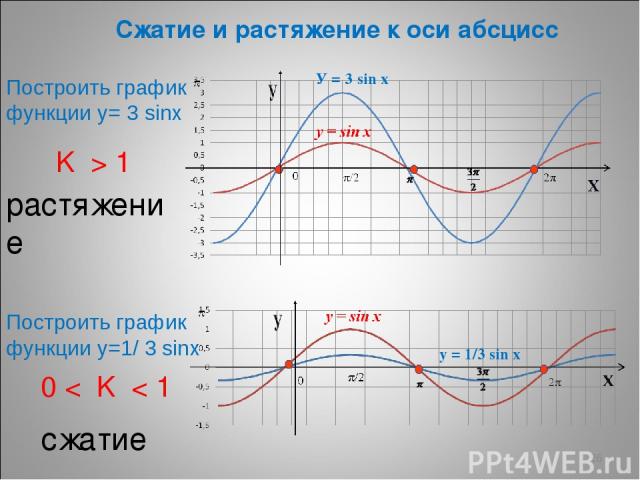
* Сжатие и растяжение к оси абсцисс K > 1 растяжение 0 < K < 1 сжатие Построить график функции у= 3 sinх Построить график функции у=1/ 3 sinх У = 3 sin x у = 1/3 sin x

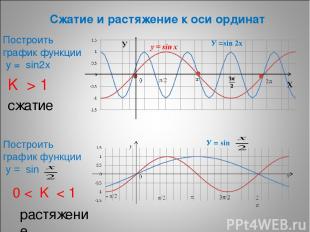
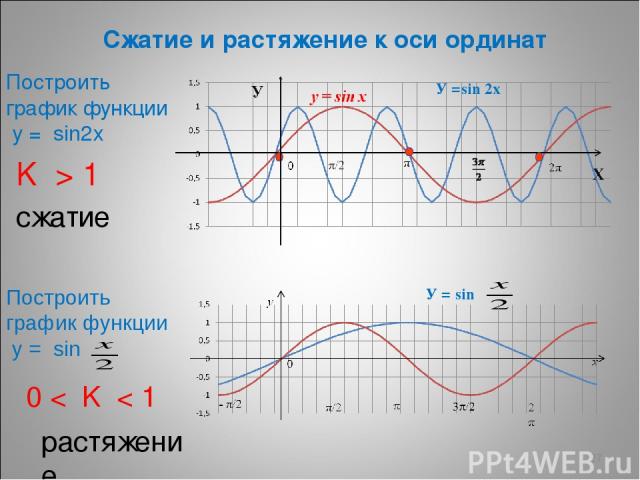
* Сжатие и растяжение к оси ординат Построить график функции у = sin2х Построить график функции у = sin K > 1 сжатие 0 < K < 1 растяжение У =sin 2х У = sin

* У х y = sin x При каких значениях х функция у=sinx принимает значение, равное 0? 1? -1? Может ли функция у=sinx принимать значение больше 1, меньше -1? При каких значениях х функция у=sinx принимает наибольшее (наименьшее) значение? Каково множество значений функции у=sinx?