Презентация на тему: Основы математической статистики

Основы математической статистики Горшков А.В. 900igr.net

Курс «Основы статистики » для студентов факультета «Связи с общественностью» рассчитан на то, чтобы дать представление об основных задачах, методах и подходах статистики, ее основах. Предполагается, что студенты знают основы курса высшей математики (элементы математического анализа: теория предела, производная, интегралы, в том числе несобственные) в пределах курса высшей математики для студентов гуманитарных факультетов университетов. Курс состоит из двух частей. Первая - элементы теории вероятностей. Вторая - основы математической статистики. Первая часть необходима для более глубокого и полного понимания основных задач и методов статистики.   Объем курса 36 часов лекций. Отчетность – зачет.

литература Шолохович Ф.А. Высшая математика в кратком изложении. Екатеринбург, УрГУ, 2003 Турецкий В.Я. Высшая математика. Екатеринбург, 1997. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая Школа, 2001, 479 с. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. Учебное пособие для студентов вузов. М.: "Высшая Школа", 1999. Математическая статистика позволяет обрабатывать результаты опытов, измерений и т.д. Математическая статистика использует методы теории вероятности. Теория вероятностей определяет законы случайности.

Шкалы измерений Номинальная. Позволяет различать предметы, например по цвету Дихотомическая. Ранговая. Позволяет упорядочить предметы Интервальная Относительная ноль соответствует полному отсутствию свойства (качества)

Случайные события Событие называется детерминированным, если в результате опыта оно происходит или не происходит наверняка. В детерминированном случае мы точно знаем, что данная причина приведет к единственному, вполне определенному следствию. Событие называется случайным, если в результате опыта мы не можем заранее предсказать - произойдет событие или нет. При этом предполагается, что опыт можно повторять неограниченное число раз при неизменных условиях. События, исход которых нельзя предсказать, но и невозможно повторять многократно, называются неопределенными.

События A и B называются несовместными, если появление одного исключает появление другого. Событие B следует из события A, если событие B происходит всегда, когда произошло событие A . Это обозначается тем же символом, что и подмножество: AÌB . Будем говорить о равенстве двух событий A и B, если из A следует B и из B следует A. Событие называется невозможным, если оно не может произойти никогда при данных условиях. Событие называется достоверным, если оно происходит всегда при данных условиях.

Пусть случайный эксперимент проводится раз n, и событие A произошло m раз. Тогда говорят, что относительная частота события A есть n(A)=m/n . Частота события связана с его вероятностью. Относительную частоту называют еще эмпирической вероятностью потому, что по частоте события мы оцениваем возможность его появления в будущем. Для любого случайного события A 0£Pn(A) £1 n - количество случайных экспериментов.

Алгебра событий Суммой двух событий A и B называется событие A+B, состоящее в том, что произошло событие A или событие B. В данном случае "или" употребляется в не исключающем значении: А или B означает, что произошло событие A, или событие B или оба этих события одновременно.

1. Если события несовместны, то вероятность суммы событий равна сумме вероятностей: P(A+B) = P(A) + P(B) 2. Если события независимы, то вероятность произведения событий равна произведению вероятностей: P(A B) = P(A) P(B) Обобщение этих теорем докажем позже. Две теоремы о вероятности суммы событий и произведении

Примеры. 1. Подбрасываем кубик. Всего исходов 6. Какова вероятность, что выпадет четное число? Благоприятны исходы 2, 4, 6. Всего 3. 3/6 2. Какова вероятность, что при первом броске выпадет 3, во втором 4? 3. Какова вероятность, что выпадет 3 или 5? Здесь вероятность суммы несовместных событий. P=1/3 4. Стрелок стреляет по мишени 4 раза. Вероятность попадания в одном выстреле 0.8. Считаем, что у него хорошие нервы – каждый следующий выстрел не зависит от предыдущего. Какова вероятность, что он промахнется ровно 1 раз?

Решение. Могут произойти следующие события: А1 промах в 1 выстреле, А2 промах во 2, А3 - в 3,или А4 - в 4. Следовательно, событие, состоящее в одном промахе, можно представить как сумму событий А= А1 + А2 +А3 +А4. Но события очевидно, несовместны и P(А)= P(А1) + P(А2 )+P(А3) +P(А4). – вероятность суммы событий равна сумме вероятностей. Но каждое событие Аi состоит в том, что одновременно, в одной серии выстрелов, произошли 4 события, причем эти события независимы по условию: Аi= Аi1Аi2 Аi3 Аi4. Но вероятность произведения независимых событий равна произведению вероятностей. Нужно найти вероятность промаха. В одном выстреле стрелок может либо попасть, либо промахнуться. Следовательно, эти события образуют полный набор и они несовместны. Но тогда вероятность промаха 1-0.8=0.2. P(Аi)=P(Аi1)P(Аi2)P(Аi3)P(Аi4.)=0.8*0.8*0.8*0.2=0.1024. Всего 0.4096

Разностью событий A и B называется событие A - B , состоящее в том, что произошло событие A и не произошло событие B. Событие B называется противоположным событию A , если оно состоит в том, что не произошло событие A Элементарные исходы 1.  не представимы в виде суммы двух других  2. попарно несовместны  3. никакие другие исходы в результате опыта произойти не могут События образуют полный набор, если они несовместны, а их сумма есть достоверное событие. Полный набор исходов называют также пространством элементарных исходов и обозначают обычно буквой W.

Комбинаторика Например, число перестановок из 6 предметов 1х2х3х4х5х6=120. Число расстановок из 6 предметов на 4 места 120/(6-4)!=120/2!=120/2=60. Число сочетаний из 6 предметов по 4 120/(4!(6-4)!)=120/(4!2!)=5х6/2=15

Например, число перестановок из 6 предметов 1х2х3х4х5х6=720. Число сочетаний из 6 предметов по 4

Классическое определение Свойства вероятности. I. Для любого случайного события А 0£P(A) £1 2. Пусть события A и B несовместны. Тогда P(A+B)=P(A)+P(B) Например: бросание кубика. Всего исходов 6, число исходов, благоприятных выпадению четного числа – 3. P(A)=1/2

Пример. В корзине 15 шаров. Из низ 5 белых и 10 черных. Какова вероятность вытащить 3 белых шара? Какова вероятность вытащить 3 черных шара? Общее число исходов – число сочетаний из 15 по 3: Число благоприятных исходов - число сочетаний из 10 по 3 Вероятность события 120/455=0,2637

Пример. Из колоды в 36 карт вытаскиваем 4. Какова вероятность, что среди них 2 короля? Решаем по классической схеме.

Вероятность суммы событий Даны два события A и B. Подсчитаем вероятность суммы событий по классической схеме. m(A) – число исходов, благоприятных только событию A. m(B) – число исходов, благоприятных только событию B. m(AB) – число исходов, благоприятных событию A и событию B. Тогда сумме событий благоприятно m(A)+ m(B)+ m(AB) исходов и вероятность суммы событий равна N – общее число исходов. С другой стороны (1) (2)

Отсюда находим формулу вероятности суммы событий Пример. Два стрелка независимо стреляют по мишени. Первый попадает с вероятностью 0.8, второй 0.7. Какова вероятность, что попадет хотя бы один? Используем полученную формулу: 0.8+0.7-0.8*0.7=0.94 Вычтем из (2) выражение (1)

Условная вероятность Пусть известно, что в результате эксперимента произошло событие B. Зная это, мы хотим подсчитать вероятность некоторого события A. Такую вероятность (при условии, что произошло событие B) называют условной вероятностью события A и обозначают P(A|B). Число исходов, благоприятных B обозначим через m(B). Условная вероятность равна Если разделить числитель и знаменатель на общее число исходов N, мы придем к формуле

Свойства условной вероятности. 1. P(A|A)=1 . 2. Если BÌA , то P(A|B)=1. 3. Для любого события B с ненулевой вероятностью P(W|B)=1, P(0|B)=0 . 4. Если события B1 и B2 несовместны, то P(A|(B1+B2))=P(A|B1)+P(A|B2) 5. Теорема умножения P(AB)=P(A|B)P(B). Определение независимости событий. Говорят, что событие А не зависит от события В, если P(A|B)=P(A).

Формула полной вероятности Теорема. Пусть события B1, B2, . . ., Bn попарно несовместны и событие A содержится в их сумме: AÌB1+B2+…+Bn. Умножим это соотношение на событие A. Тогда в левой части получим A2=A, в правой A(B1+B2+…+Bn) и A=A(B1+B2+…+Bn) Вложение перешло в равенство. Вычислим вероятность от обеих частей P(A)=P(AB1)+P(AB2)+…+P(ABn) Вероятности произведений заменим P(AB1)=P(A|B1)P(B1) Тогда вероятность события A можно вычислить по следующей формуле: P(A)=P(A|B1)P(B1)+ P(A|B2)P(B2)+…+ P(A|Bn)P(Bn)

Пример. Имеется 3 группы корзин. Корзин типа B1 – 5 Корзин типа B2 – 3 Корзин типа B3 – 2 В каждой корзине типа B1 10 белых 5 черных шаров. В каждой корзине типа B2 5 белых 10 черных шаров. В каждой корзине типа B3 10 белых 15 черных шаров. Какова вероятность из выбранной наугад корзины выбрать белый шар? Решение. Вероятность выбрать белый шар из B1 P(A|B1)=10/15 Вероятность выбрать белый шар из B2 P(A|B2)=5/15 Вероятность выбрать белый шар из B3 P(A|B3)=10/25 Вероятность выбрать корзину первой группы P(B1)=5/10 Вероятность выбрать корзину второй группы P(B2)=3/10 Вероятность выбрать корзину третьей группы P(B3)=2/10 Подставляем числа в формулу

Формула Байеса Теорема. Пусть события B1, B2, . . ., Bn попарно несовместны и событие A содержится в их сумме: AÌB1+B2+…+Bn. Тогда при k=1,2,…,n справедлива формула

Пример Те же самые условия. Случайно извлечен белый шар. Какова вероятность, что он извлечен из первой группы корзин? Т.е. Мы фактически хотим найти вероятность P(B1|A). Решение. P(A)=0.513333 (из предыдущей задачи) P(B1)=5/10, P(A|B1)=10/15. После подстановки получим

Схема испытаний Бернулли Пусть в результате некоторого случайного испытания может произойти или не произойти определенное событие А. Если событие произошло, будем называть испытание успешным, а само событие – успехом. Испытание повторяется n раз. При этом соблюдаются следующие условия: вероятность успеха P(A)=p в каждом испытании одна и та же; результат любого испытания не зависит от исходов предыдущих испытаний. Такая последовательность испытаний с двумя исходами (успех/ неуспех) называется последовательностью независимых испытаний Бернулли или – схемой испытаний Бернулли.

Формула Бернулли вероятности k успехов в n независимых испытаниях. В серии из n испытаний должно одновременно произойти k успехов и n-k - «неуспехов». Вероятность успеха p, «неуспеха» q=1-p, так как для одного испытания события «успех/неуспех» образуют полную набор. Но тогда вероятность одной серии равна Сколько может быть различных серий? Очевидно, сколькими способами мы можем расставить k успехов на n мест. Это число расстановок. Но все успехи одинаковы. Следовательно, число серий равно числу сочетаний из n по k. Серии между собой, очевидно, несовместны, так как отличаются положением хотя бы одного успеха. Следовательно, вероятность суммы равна сумме вероятностей:

Пример. Подбрасываем 10 раз кубик. Какова вероятность, что пятерка выпадет ровно 4 раза? Решение. Схема испытаний Бернулли. p=1/6, q=1-1/6=5/6.

Задача 2. Какова вероятность, что число успехов будет от k1 до k2? Очевидно, что цепочки с числом успехов k1, k1+1,…,k2 представляют собой несовместные события. Но тогда вероятность суммы равна сумме вероятностей и Пример. Какова вероятность, что из 10 бросаний монеты орел выпадет от 4 до 6 раз? Решение. Очевидно, что события выпал орел 4 раза, 5 раз, 6 раз несовместны. Следовательно, вероятность суммы равна сумме вероятностей:

Локальная теорема Лапласа Если вероятность p появления события A в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие А появится в n испытаниях ровно k раз, приближенно равна где

Интегральная теорема Лапласа Если вероятность p появления события A в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие А появится в n испытаниях от k1 до k2 раз, приближенно равна где

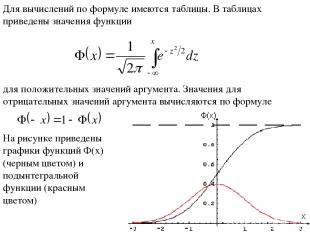
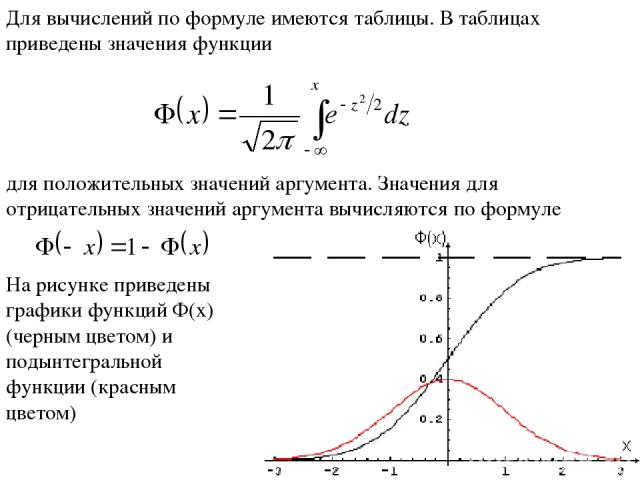
Для вычислений по формуле имеются таблицы. В таблицах приведены значения функции для положительных значений аргумента. Значения для отрицательных значений аргумента вычисляются по формуле На рисунке приведены графики функций Ф(x) (черным цветом) и подынтегральной функции (красным цветом)

Если -x1=x2=x, то справедлива формула

Пример 1. Какова вероятность, что из 100 подбрасываний кубика четверка выпадет ровно 30 раз. n=100, m=30, p=1/6, q=1-1/6=5/6

Пример 2. Какова вероятность, что из 100 подбрасываний кубика 4 выпадет от m1=15 до m2=25 раз.

Задача 3 . Сколько раз нужно подбросить кубик, чтобы частота отличалась от вероятности не более чем на 0.005 с вероятностью 0.9? Решение. Основная формула. Роль x1, x2 теоремы Лапласа играют Из теоремы Лапласа

Подставив числа, получим уравнение относительно n По таблице ищем значение аргумента функции Лапласа такое, что ее значение равно 0.95. Это 1.65. Отсюда находим n n=15125

Конечная случайная величина Часто исход случайного эксперимента выражается некоторым числом. Когда каждому элементарному исходу случайного эксперимента мы ставим в соответствие некоторое число xk, то мы определяем на множестве событий некоторую числовую функцию. Набор чисел может быть конечным или бесконечным: это зависит от количества элементарных исходов эксперимента. Неформально говоря, такое число, принимающее случайные значения, и называется случайной величиной. Например. Подбрасываем монетку. Поставим в соответствие «орлу» - 1 , «решке» - 0. Можно наоборот: «орлу» - 0 , «решке» - 1. А можно симметрично: «орлу» - -1 , «решке» - 1. Каждой грани кубика ставим в соответствие число очков, которое нарисовано на грани. Картам, в зависимости от игры назначают то или иное число очков.

Случайная величина, принимающая конечное число значений, называется конечной случайной величиной. Пусть пространство элементарных исходов конечно: W={w1,w2,...,wn }. Вероятность P любого случайного события, связанного с данным экспериментом, полностью определяется набором неотрицательных чисел pi=P(wi) , i=1,2,…,n, таких, что p1+p2+…+pn=1.

Такое вероятностное пространство можно представить с помощью таблицы Функцию x(w), заданную на конечном числе аргументов, также задаем табличным способом: Будем предполагать, что все числа xk различны. Случайная величина принимает значение xk , если произошел исход wk, вероятность которого равна pk Точнее: вероятность события {x(wk)=xk} равна pk Конечная случайная величина полностью определяется своими значениями и их вероятностями.

Поэтому таблица часто отождествляется с самой случайной величиной и называется законом распределения конечной случайной величины. Часто закон распределения записывают короче Например: поставим в соответствие выпаданию орла 1, а решке –1. Можно иначе: орлу –0, решке 1. Возможны иные варианты.

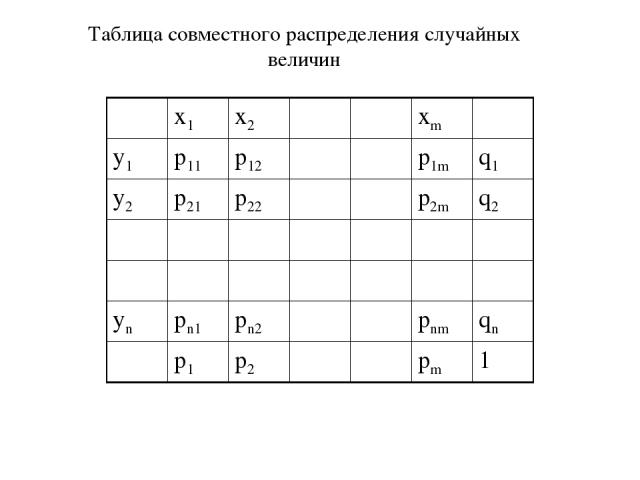
Совместное распределение случайных величин Пусть заданы две конечные случайные величины: Событие {x=xi}{h=yj} состоит в том, что одновременно случайная величина x принимает значение xi , а случайная величина h – значение yj . Назовем вероятности таких событий совместными вероятностями и обозначим их через pij:

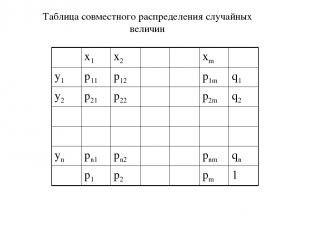
Таблица совместного распределения случайных величин x1 x2 xm y1 p11 p12 p1m q1 y2 p21 p22 p2m q2 yn pn1 pn2 pnm qn p1 p2 pm 1

Две конечные случайные величины называются независимыми, если события {x=xi} и {h=yj} независимы при всех i=1,2,. . .,m и j=1,2, .., n . В противном случае случайные величины зависимы. Для независимых случайных величин совместное распределение строится по известным распределениям величин x и h: Пусть заданы две конечные случайные величины:

Произведением этих случайных величин называется случайная величина x h, значениями которой являются всевозможные произведения xiyj с теми же вероятностями pij . Пусть заданы две конечные независимые случайные величины: Их суммой называется случайная величина x + h , значениями которой являются всевозможные суммы с совместными вероятностями Такие случайные величины называются биномиальными. Вычислим закон распределения x + h. Возможные значения суммы: 0- принимается с вероятностью q2, значение 1 – принимает в двух случаях с вероятностями pq и значение 2 – с вероятностью p2.

В результате получим таблицу Этот результат можно обобщить на любое число слагаемых. Теорема. Пусть x1, x2, . . . , xn независимые бернулливые случайные величины. Тогда их сумма есть биномиальная случайная величина Иная трактовка: если xk – число успехов в k-ом испытании, то число успехов в n испытаниях есть их сумма.

Математическое ожидание Математическим ожиданием конечной случайной величины называется число Понятие математического ожидания упрощенно можно представить иначе. Пусть z1, z2, z3,…, zk - результаты некоторого испытания, описываемого случайной величиной x. Среднее значение случайной величины за большое число k испытаний будет

Например, при бросании кубика вероятность выпадения каждой грани равна 1/6. Тогда математическое ожидание числа очков равно Среди этих значений соберем все равные x1, x2,…. В результате получится Но отношение есть частота появления значения xj. А частота при большом числе опытов близка к вероятности. В итоге получаем формулу из определения.

Математическое ожидание обладает следующими свойствами. 1. Математическое ожидание постоянной равно ей самой: 2. Если случайная величина принимает только неотрицательные значения, то 3. Константу можно выносить за знак математического ожидания: 4. Математическое ожидание суммы (разности) случайных величин равно сумме (разности) их математических ожиданий:

5. Для любой случайной величины справедливо равенство Операция вычитания математического ожидания из случайной величины называется центрированием 6. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий Математическое ожидание биномиальной случайной величины. Числовое значение величины – кол-во успехов в серии испытаний. Одно испытание можно рассматривать как серию из одного испытания. Назначим успеху числовое значение 1, а неуспеху – 0. Следовательно, математическое ожидание в одном опыте равно p. Представим серию опытов как сумму отдельных испытаний. Тогда по свойству математического ожидания M=np.

Дисперсия Дисперсией конечной случайной величины x называется число по определению математического ожидания, дисперсия вычисляется по следующей формуле называется среднеквадратичным отклонением или стандартным отклонением случайной величины

Свойства дисперсии Дисперсия любой случайной величины неотрицательна Dx>0 При этом Dx=0 тогда и только тогда, когда случайная величина постоянна. 2. Константа выносится из-под знака дисперсии с квадратом 3. Сдвиг на константу не меняет дисперсии: 4. Дисперсия суммы независимых случайных величин равна сумме их дисперсий: (x и h независимы )

5. Дисперсия равна "среднему квадрата минус квадрат среднего": Дисперсия биномиальной случайной величины. Вычисление проведем по той же схеме, что и для математического ожидания. Биномиальная случайная величина есть сумма n независимых бернуллиевых величин. Но тогда используем формулу дисперсии суммы: Но и

Случайная величина называется стандартизованной (по отношению к x) или просто стандартизацией x Стандартизованная случайная величина имеет нулевое математическое ожидание и единичную дисперсию. Пример. Дисперсия при бросании кубика. Математическое ожидание 3.5. Считаем математическое ожидание квадрата случайной величины: Среднее квадратичное отклонение Таблица стандартизованных значений -1.4639 -0.8783 -0.2928 0.2928 0.8783 1.4639

Задача. Проводится лотерея. Разыгрывается 50 билетов по 1 рублю. Известно, что среди билетов 1 выигрывает 30 руб., 2 – по 10 руб. Приобретено 2 билета. Вычислить математическое ожидание чистого дохода.

Коэффициент корреляции Ковариацией двух случайных величин x и h (или ковариацией между x и h) называется число Из определения следуют некоторые простые свойства ковариации 2. Ковариаиия коммутативна: 1. 3. Ковариация суммы случайных величин 4. Ковариация случайной величины с собой

Следующее свойство важно при оценке степени зависимости двух случайных величин. 5. Если случайные величины x и h независимы, то их ковариация равна нулю. Для независимых величин x и h их центрированные величины также независимы. Поэтому Ковариация стандартизованных величин называется коэффициентом, корреляции между случайными величинами x и h Предполагается, что случайные величины x и h имеют ненулевые дисперсии

свойства коэффициента корреляции: 2. Коэффициенты корреляции между x и h и между их стандартизациями совпадают 1. 3. Коэффициент корреляции всегда по модулю меньше 1 4. Если x и h независимы, то 5. Коэффициент корреляции равен +1 или -1 тогда и только тогда, когда случайные величины линейно зависимы:

Примеры. Даны таблицы распределения. Найти коэффициенты корреляции Вычислительная формула P 0.2 0.2 0.2 0.2 0.2 X -2 -1 0 1 2 Y 1 0 -1 -2 -3 P 0.2 0.2 0.2 0.2 0.2 X -2 -1 0 1 2 Y 4 1 0 1 4 P 0.2 0.2 0.2 0.2 0.2 X -2 -1 0 1 2 Y 1 2.5 4 5.5 6 P 0.2 0.2 0.2 0.2 0.2 X -2 -1 0 1 2 Y 1 0 1 2 1

Mx=0, Dx=2, MY=1, DY=2 MXY=-2, R=-1 Mx=0, Dx=2, MY=3.8, DY=3.46 MXY=2.6, R=0.9884 Mx=0, Dx=2, MY=2, DY=2.8 MXY=0, R=0 Mx=0, Dx=2, MY=1, DY=0.4 MXY=0.4, R=0.4472

Функция распределения Функция действительной переменной называется функцией распределения случайной величины x . Свойства функции распределения 1. 2. 3. При любом х выполняется неравенство. Это справедливо, поскольку функция распределения есть вероятность 4. Функция распределения есть неубывающая функция.

6. Функция распределения непрерывна слева, то есть

7. Для любой непрерывной случайной величины 8. Функция распределения непрерывной случайной величин имеет вид

Функция неотрицательна при всех x 2. Условие нормировки. Справедливо равенство Свойства плотности функции распределения 3. В точках непрерывности плотность вероятности равна производной функции распределения:

Математическим ожиданием непрерывной случайной величины называется число (если соответствующий интеграл существует). Дисперсия вычисляется через интеграл: (если интеграл существует).

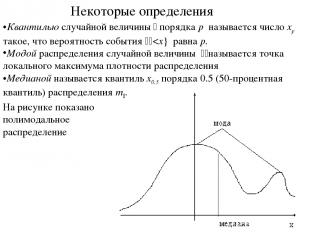
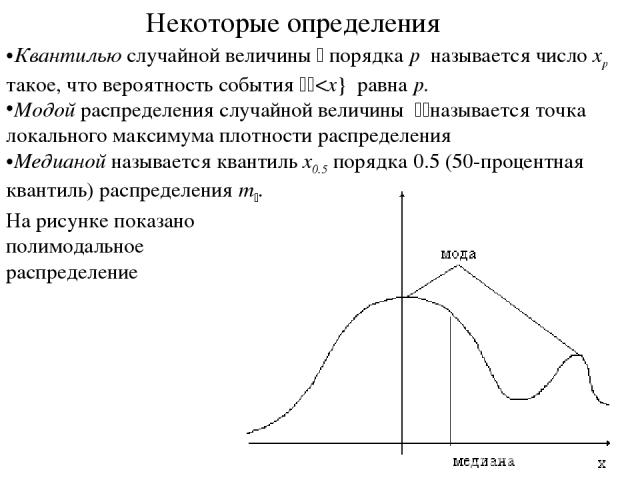
Квантилью случайной величины x порядка p называется число xp такое, что вероятность события {x

Биномиальное распределение где Распределение Пуассона. Получается как предельное при очень большом числе испытаний маловероятных событий.

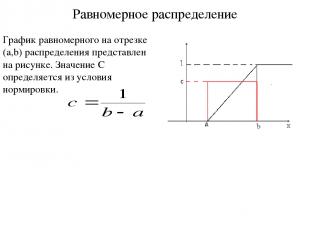
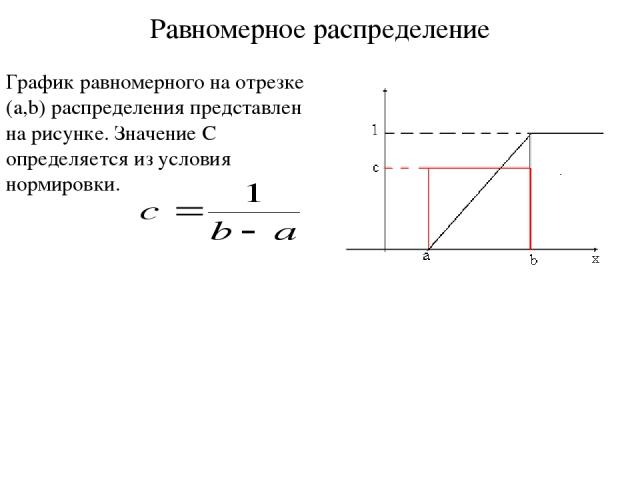
Равномерное распределение График равномерного на отрезке (a,b) распределения представлен на рисунке. Значение C определяется из условия нормировки.

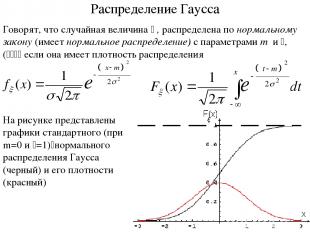
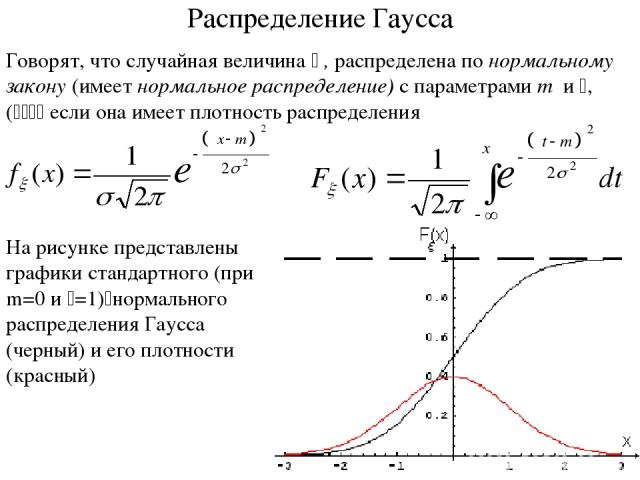
Говорят, что случайная величина x , распределена по нормальному закону (имеет нормальное распределение) с параметрами m и s, (s>0) если она имеет плотность распределения Распределение Гаусса На рисунке представлены графики стандартного (при m=0 и s=1) нормального распределения Гаусса (черный) и его плотности (красный)

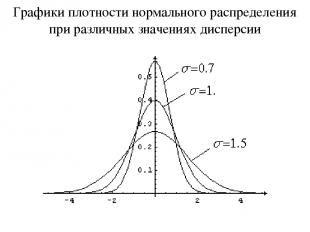
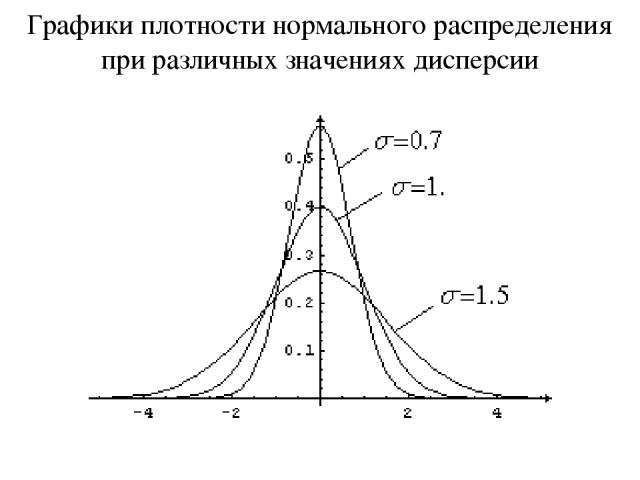
Графики плотности нормального распределения при различных значениях дисперсии

Свойства нормального распределения график симметричен относительно прямой x=m; функция достигает максимума в точке x=m; график приближается к нулю при возрастании |x| Нормальное распределение обозначают N(m,s). Нормальное распределение с параметрами m=0, s=1 называется стандартным нормальным распределением и задается плотностью

Пусть x~N(m,s). Тогда квантиль xp случайной величины x связана с квантилью стандартного нормального распределения следующим соотношением:

Законы больших чисел Теорема Бернулли

Центральная предельная теорема Ляпунова Пусть случайные величины X1, X2, …, Xn независимы, одинаково распределены с математическим ожиданием M и конечной дисперсией s2. Тогда справедливо предельное соотношение Сколь угодно близка к единице, если n достаточно велико.

Статистика Генеральной совокупностью называется вся совокупность исследуемых объектов Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных из генеральной совокупности объектов Объемом совокупности называют число объектов этой совокупности Способы формирования выборочной совокупности Повторный – после измерений объект возвращают в генеральную совокупность Бесповторный – после измерений объект в генеральную совокупность не возвращается Выборка должна быть репрезентативной - представительной. Для этого объекты из генеральной совокупности должны отбираться случайно.

Простой случайный отбор – объекты извлекают по одному из всей генеральной совокупности Типический отбор - объекты отбирают не из всей генеральной совокупности, а из каждой ее «типической части» Механический отбор – генеральную совокупность делят механически на несколько групп и из каждой группы отбирают один объект Серийный отбор – объекты из генеральной совокупности отбирают не по одному, а сериями, которые подвергают сплошному обследованию. На практике, как правило, используется смешанная схема.

Выборка и ее обработка Совокупность пар (zi, ni ) называют статистическим рядом выборки. Часто его представляют в виде таблицы – в первой строке zi, во второй ni. Величина ni = ni /n называется относительной частотой Накопленная частота значения zi равна n1+n2+…+ni. Относительная накопленная частота n1+n2+…+ni

Удобнее всего разбивать на равные интервалы. При этом считается, что правая граница интервала принадлежит следующему интервалу. Последний интервал включает правую границу. После этого подсчитываются частоты – количество ni элементов выборки, попавших в i-й интервал. Получающийся статистический ряд в первой строке содержит середины интервалов группировки zi, а во второй строке -частоты ni, попадания в соответствующий интервал. Наряду с частотами подсчитываются относительные частоты ni, накопленные частоты и накопленные относительные частоты. Результаты обычно сводятся в таблицу частот группированной выборки, а процесс формирования такой таблицы называется частотной табуляцией выборки.

Пример Дана выборка 0,0473 0,0543 0,0561 0,0989 0,1107 0,1112 0,1204 0,1647 0,2030 0,2138 0,2147 0,2463 0,2725 0,2734 0,3029 0,3222 0,3389 0,3841 0,3909 0,4037 0,4071 0,4173 0,4238 0,4308 0,4451 0,5382 0,5454 0,5472 0,6124 0,6320 0,6417 0,6776 0,6908 0,7399 0,7715 0,7853 0,8038 0,8174 0,8201 0,8287 0,8693 0,8704 0,8704 0,8718 0,8965 0,9025 0,9130 0,9366 0,9629 Она содержит 49 чисел в отрезке [0,1]. Все числа различны.

Проведем группировку. Разобьем отрезок на 10 полуинтервалов [0,0.1),[0.1,0.2),…[0.8,0.9),[0.9,1.0]. Подсчитаем, сколько элементов выборки попало в каждый интервал и получим статистический ряд 0.05 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 0.95 4 4 6 5 6 3 5 3 9 4 Обработку этого примера продолжим в дальнейшем.

Эмпирическая функция распределения Это распределение называется выборочным, или эмпирическим, распределением. Как и для любой конечной случайной величины, для эмпирической случайной величины можно построить ступенчатую функцию распределения; она называется выборочной функцией распределения. Кроме того, можно вычислить все числовые характеристики выборочной случайной величины xn- математическое ожидание, дисперсию, СКО, медиану и т.д.

Оценки параметров распределения Точечные оценки

Индекс п в обозначении оценки напоминает, что она получена по выборке объема n, «звездочка» показывает, что это не истинное значение параметра, а его оценка. Произвольную функцию от выборки называют еще статистикой.

Несмещенная оценка называется наиболее эффективной (или просто эффективной), если она имеет минимальную дисперсию среди всех несмещенных оценок данного параметра.

ОЦЕНКА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ

Поскольку каждое значение из выборки есть случайная величина с функцией распределения, то вероятность успеха равна p=F(x) . Число успехов равно mn(x) , а относительная частота успеха равна mn(x)/n и совпадает с выборочной функцией распределения.

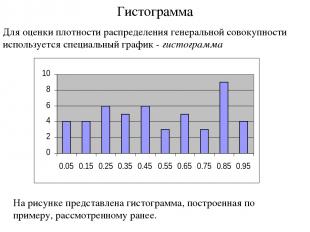
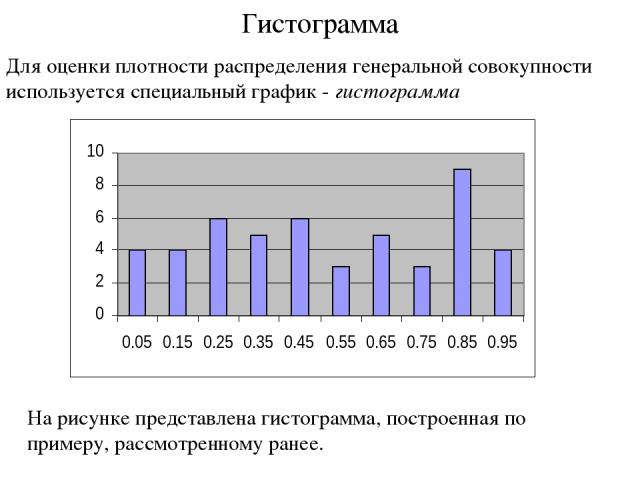
Гистограмма Для оценки плотности распределения генеральной совокупности используется специальный график - гистограмма На рисунке представлена гистограмма, построенная по примеру, рассмотренному ранее.

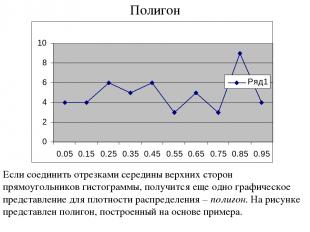
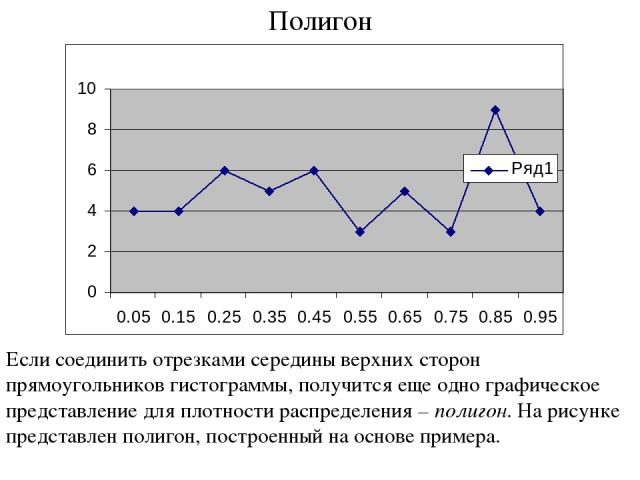
Полигон Если соединить отрезками середины верхних сторон прямоугольников гистограммы, получится еще одно графическое представление для плотности распределения – полигон. На рисунке представлен полигон, построенный на основе примера.

Точечная оценка математического ожидания Выборочное среднее дает несмещенную и состоятельную оценку математического ожидания

Точечная оценка дисперсии Вычислим математическое ожидание выборочной дисперсии. Для этого преобразуем выражение для s2 (через М обозначено математическое ожидание генеральной совокупности):

Приведенное выражение дает состоятельную несмещенную оценку дисперсии генеральной совокупности Для вычисления выборочной дисперсии можно вывести более удобную формулу

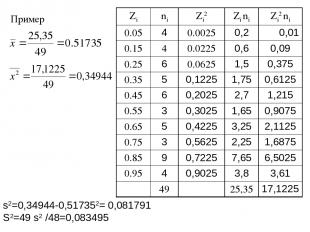
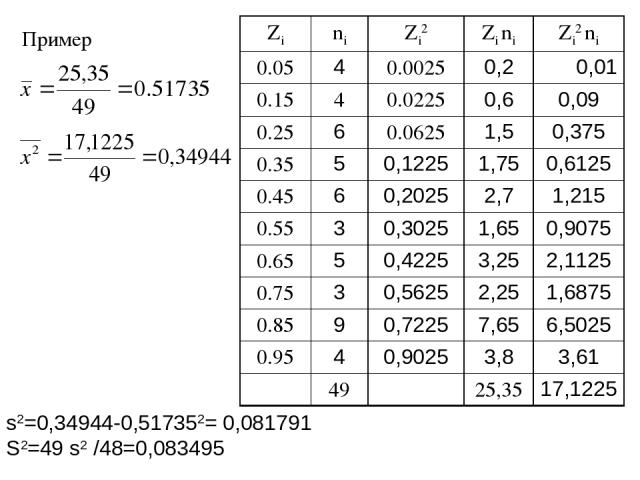
Пример s2=0,34944-0,517352= 0,081791 S2=49 s2 /48=0,083495 Zi ni Zi2 Zi ni Zi2 ni 0.05 4 0.0025 0,2 0,01 0.15 4 0.0225 0,6 0,09 0.25 6 0.0625 1,5 0,375 0.35 5 0,1225 1,75 0,6125 0.45 6 0,2025 2,7 1,215 0.55 3 0,3025 1,65 0,9075 0.65 5 0,4225 3,25 2,1125 0.75 3 0,5625 2,25 1,6875 0.85 9 0,7225 7,65 6,5025 0.95 4 0,9025 3,8 3,61 49 25,35 17,1225

Выборочные мода, медиана, квантили Выборочные мода, медиана и квантиль легко определяются по упорядоченной, но не сгруппированной выборке. Медиана – середина вариационного ряда. Справа и слева располагается одинаковое число значений выборки. Мода– наиболее часто встречающееся значение выборки. Квантиль – левее должно располагаться кол-во значений, соответствующее индексу квантили. Например, для квантили x0.8 Левее должно располагаться 80% значений выборки. В нашем примере: мода=0.85, медиана= 0,4451, x0..8= 0,8287 – левее должно располагаться 49*0.8=39.2 39 значений выборки.

Интервальные оценки Интервальная оценка – некоторый интервал [a,b]. По заданной выборке мы должны найти a(x1,x2,…,xn) и b(x1,x2,…,xn) такие, чтобы накрывали неизвестное значение параметра J с заданной вероятностью g – уровнем значимости. Уровень значимости выбирается в зависимости от необходимой точности решения задачи. Обычно 0.9 – 0.99. Считается 0.9 – средняя точность, 0.99 – высокая, 0.999 – очень высокая. Часто доверительный интервал строится симметричным относительно точечной оценки. В дальнейшем будем предполагать, что выборка {x1,x2,…,xn} получена из нормально распределенной генеральной совокупности: xi~N(m,s) и при различных условиях требуется найти доверительные интервалы для параметров m и s2.

Доверительный интервал математического ожидания Случай 1. Считаем, что известна дисперсия генеральной совокупности s2.

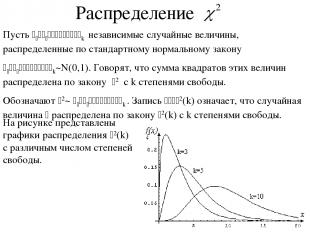
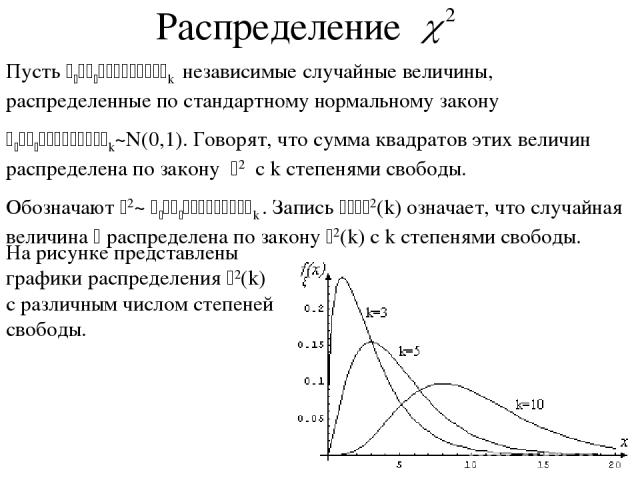
Пусть x1,x2, . . .,xk независимые случайные величины, распределенные по стандартному нормальному закону x1,x2, . . .,xk~N(0,1). Говорят, что сумма квадратов этих величин распределена по закону c2 с k степенями свободы. Обозначают c2~ x1,x2, . . .,xk . Запись x~ c2(k) означает, что случайная величина x распределена по закону c2(k) с k степенями свободы. Распределение

Свойства распределения c2 . Случайная величина имеет нулевую плотность распределения при x£0. При большом числе степеней свободы k распределение c2(k) близко к нормальному. Математическое ожидание случайной величины, распределенной по закону k степенями свободы, равно k: M c2(k)=k

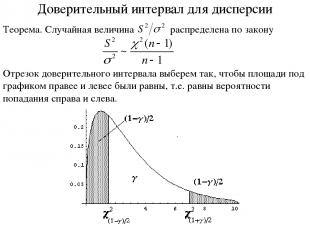
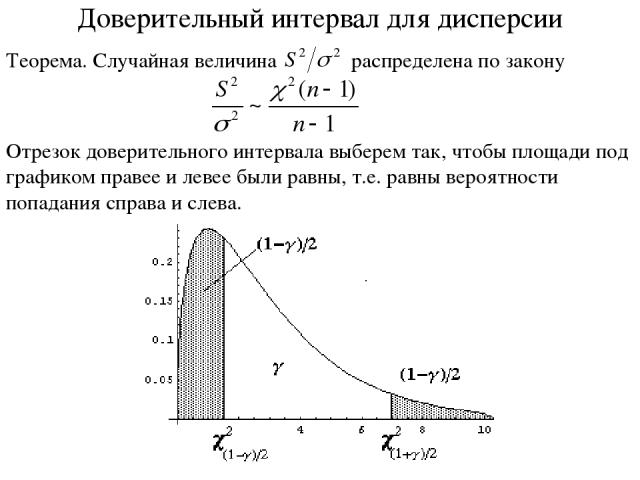
Доверительный интервал для дисперсии

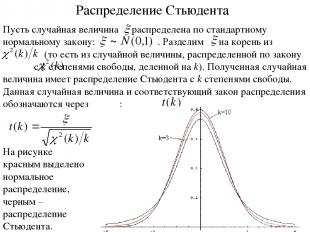
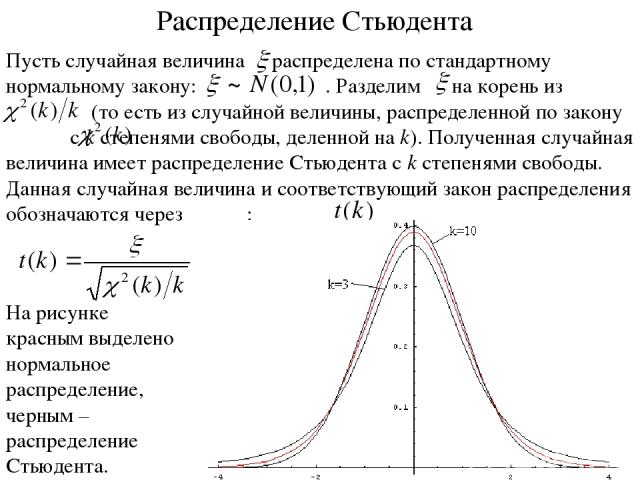
Распределение Стьюдента На рисунке красным выделено нормальное распределение, черным – распределение Стьюдента.

Свойства распределения Стьюдента Распределение Стьюдента симметрично, причем Mt(k) = 0. При больших k распределение Стьюдента близко к стандартному нормальному распределению N(0,1).

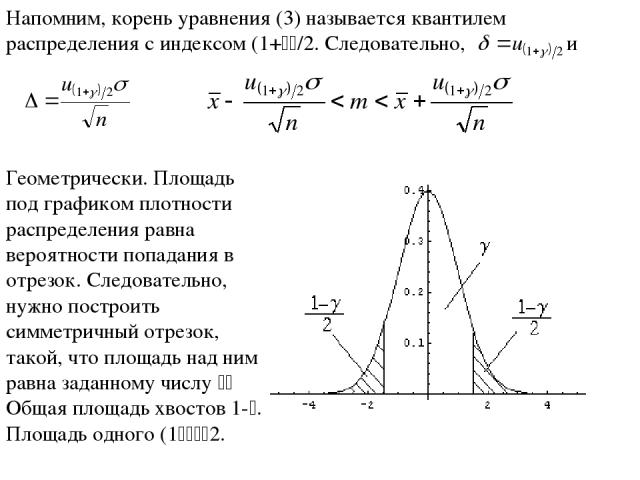
Доверительный интервал математического ожидания. Случай 2. Случайная величина U распределена по нормальному закону

Пример m=0.51735, s=0,288955, n=49. После вычислений получим 0,0809074. Интервал будет 0.51735- 0,0809074

Пример. Интервал для дисперсии Находим интервал 0,056131

Основы теории проверки статистических гипотез Статистической гипотезой называется предположение относительно параметров или вида распределения наблюдаемой случайной величины . Гипотеза называется простой, если она однозначно определяет распределение генеральной совокупности. В противном случае гипотеза называется сложной. Гипотезы о параметрах распределения. Эти гипотезы представляют собой предположение о значении некоторых параметров распределения генеральной совокупности. 2. Гипотезы о виде распределения. Эти гипотезы более о6щего характера выдвигаются в условиях недостаточной информации о генеральной совокупности. Проверяемая гипотеза называется нулевой гипотезой и обычно обозначается H0. Наряду с H0 рассматривают альтернативную (конкурирующую) гипотезу H1.

Например: выдвигается гипотеза о значении математического ожидания H0 : m=a Возможные альтернативные H1: m¹a, m>a, m

Формирование решающего правила опирается на ту же идею, которая используется при построении доверительных интервалов. Ищется случайная величина (так называемая статистика критерия), удовлетворяющая двум основным требованиям: 1) ее значение можно посчитать, используя только выборку; 2) ее распределение известно в предположении, что нулевая гипотеза верна. После того, как такая статистика выбрана, на числовой оси выделяется область, попадание в которую для этой случайной величины маловероятно (критическая область). Малая вероятность задается числом a (уровнем значимости). Основной принцип проверки гипотез состоит в следующем. Маловероятное событие считается невозможным. Событие с большой вероятностью считается достоверным. Общая схема проверки гипотез

Построение решающего правила на основе критерия значимости можно разбить на следующие основные шаги. 1. Сформировать нулевую H0 и альтернативную H1 гипотезы. 2. Назначить уровень значимости a . 3. Выбрать статистику Z критерия для проверки гипотезы H0 . 4. Найти плотность распределения статистики fz(x)=fz(x|H0) критерия в предположении, что гипотеза H0 верна. 5. Определить на числовой оси критическую область Vc из условия P(ZÎ Vc| H0)= a (условная вероятность того, что Z попадает в область Vc, при условии, что гипотеза H0 верна). Область R\Vc в этом случае называется областью принятия решения. Условия, задающие критическую область, называются просто критерием. 6. По выборке вычислить выборочное значение Zs статистики критерия.

7. Принять решение: • если ZsÎVc , гипотеза H0 отклоняется (то есть принимается гипотеза H1): • если ZsÎR\Vc, гипотеза H0 не отклоняется. Принятое решение носит вероятностный, случайный характер. Поэтому обычно применяют более осторожные формулировки. Вместо того чтобы сказать “гипотеза отклоняется, говорят: "данные эксперимента не подтверждают гипотезу “, “гипотеза не согласуется с экспериментом” Значение уровня значимости не определяет критическую область однозначно.

Пример: проверка гипотезы о математическом ожидании

Пример 2. Иной вариант альтернативной гипотезы

Ошибки при проверке статистических гипотез Принятие решения на основе статистического критерия носит случайный характер. Возможны следующие ситуации. Гипотеза верна H0, и она не отвергается. Гипотеза H0 верна, но она отвергается. В этом случае говорят, что допущена ошибка I рода. Поскольку нулевая гипотеза верна, статистика Z действительно имеет то распределение, на основании которого принималось решение. Тем не менее выборочное значение статистики попало в критическую область. Вероятность этого события по определению равна уровню значимости a. Вероятность ошибки I рода равна уровню значимости критерия. (это риск производителя) 3. Гипотеза H0 неверна, и она отвергается. 4. Гипотеза H0 неверна, но она не отвергается. Тогда говорят, что допущена ошибка II рода. (это риск потребителя)

В этой ситуации выборочное значение попало в область принятия решения, тогда как гипотеза на самом деле неверна. Если распределение статистики Z известно и в предположении, что верна альтернативная гипотеза H1 , то можно посчитать вероятность ошибки II рода: это условная вероятность того, что Z попадает в область R\Vc при условии, что верна гипотеза H1 . Вероятность ошибки II рода обычно обозначают через b Для оценки вероятности ошибки второго рода нужно знать функцию распределения в предположении, что альтернативная гипотеза верна.

Проверка гипотезы о функции распределения

Понятие о факторном анализе Пусть результаты наблюдений составляют k независимых выборок (групп), полученных из k нормально распределенных генеральных совокупностей, которые имеют, вообще говоря, различные средние m1,m2,…,mk . Каждая группа содержит nj значений, j=1,2,…,k . Общее число наблюдений равно n: n1+n2+…nk=n Проверяется гипотеза о равенстве средних во всех k выборках: H0: m1=m2=…=mk Нулевая гипотеза является сложной: предполагается лишь, что математические ожидания совпадают. Альтернативная гипотеза состоит в том, что хотя бы две выборки имеют различные средние. Обозначим через xij i-й элемент j-й выборки, i=1,2,…,nj , j=1,2,…,k .

Пример Даны две выборки {1.5, 2.5, 2., 1.7, 2.25} и {2., 1.8, 2.2, 2.5, 1.7, 1.6} Выборочное среднее для первой 1.99, для второй 1.96667. Значимо ли различие? Оценки дисперсии S1=0.163, S2=0.114667 Генеральное среднее 1.97727, генеральная дисперсия 0.122682