Презентация на тему: Формулы и правила дифференцирования

Формулы и правила дифференцирования
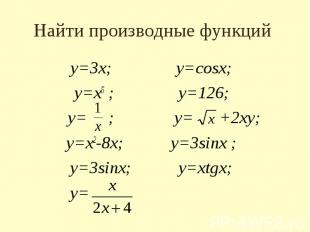
Найти производные функций у=3х; у=cosx; у=х5 ; у=126; у= ; у= +2ху; у=х2-8х; у=3sinx ; у=3sinx; у=хtgх; у=

Укажите, какой формулой можно задать функцию y=f(x), если eё производная равна: 12х; -sinx; 9; cosx-5х2; 10х9

Разделите предложенные высказывания на две группы – верные и неверные: а) Производная какой-либо функции – это совершенно новая функция, никак не связанная с исходной функцией; б) Производная функции, вычисленная в данной точке, выражает угловой коэффициент касательной; в) Процедуру отыскания производной называют дифференцированием функции; г) Если функция непрерывна в точке х=a, то она и дифференцируема в этой точке; д) Формулы дифференцирования – это формулы производных функций; е) Если известна производная, то можно найти и саму функцию.

Ответы к тесту Неверные ответы: а, г; Верные ответы: б, в, д, е.

Ответы к задачам III(2) а) =5 ; = ; = ; = .
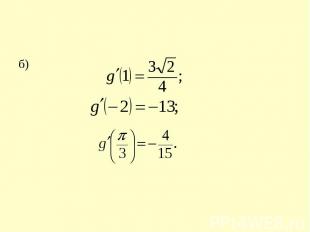
б)
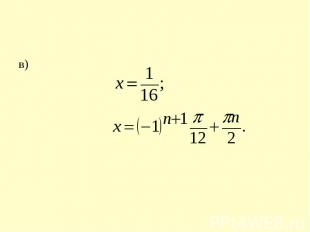
в)
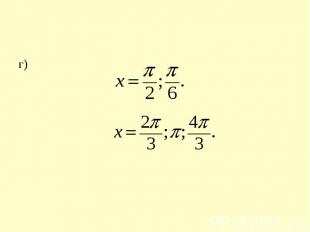
г)
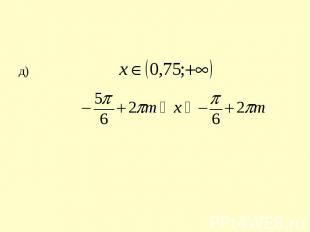
д) x

Спасибо за урок


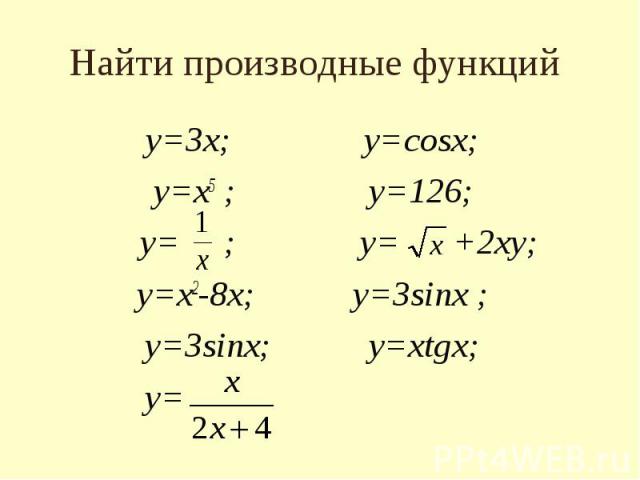




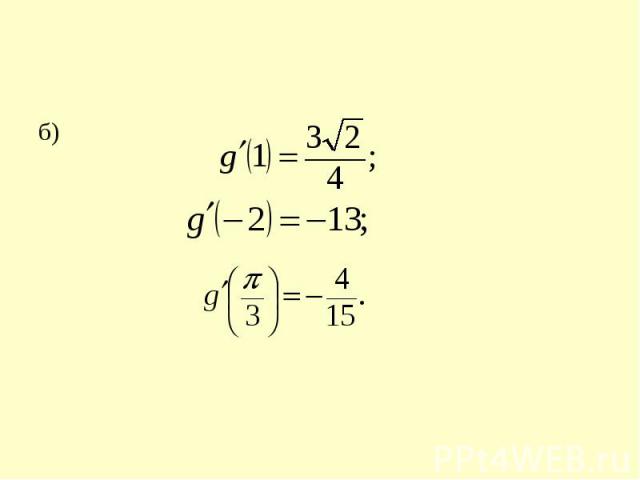
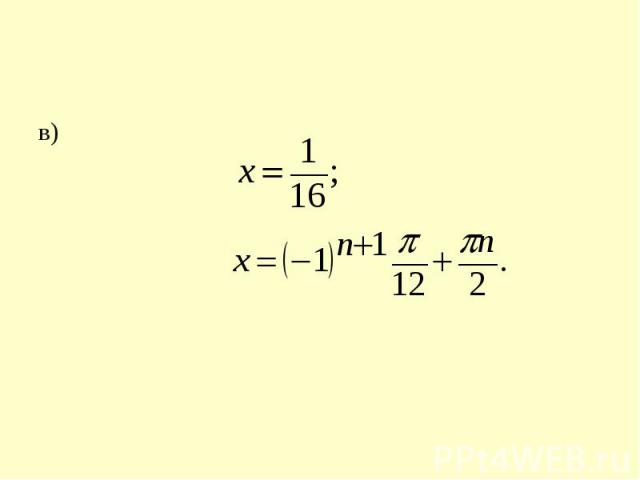
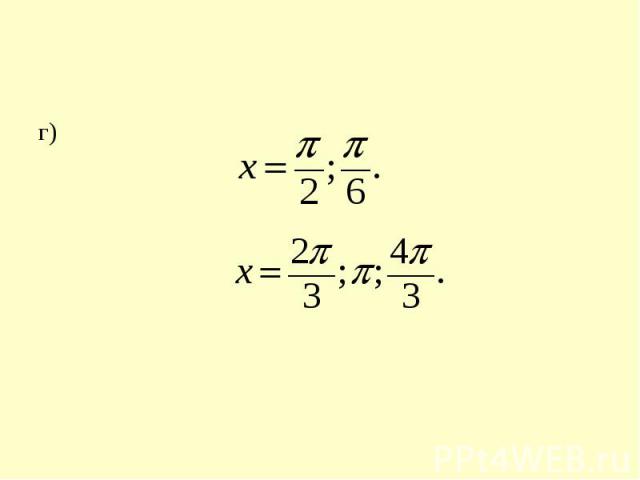
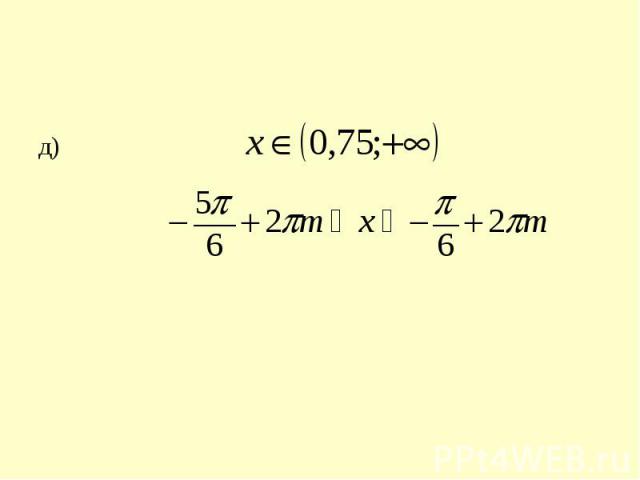



![Звуки [т'] и [т]. Буквы Т, т](https://fs1.ppt4web.ru/images/95377/148046/218/img0.jpg)

!["Согласные звуки [ф], [ф']. Буква "Ф, ф""](https://fs1.ppt4web.ru/images/95377/148043/218/img0.jpg)
![Согласные звуки [п], [п'], буква П, п](https://fs1.ppt4web.ru/images/95377/148042/218/img0.jpg)
![Согласные звуки [к], [к'], буквы "К, к"](https://fs1.ppt4web.ru/images/95377/148041/218/img0.jpg)




