Презентация на тему: Сфера, описанная вокруг многогранника

Определение: Многогранник называется вписанным в сферу (вписанным в шар), если все вершины многогранника принадлежат этой сфере. Определение: Многогранник называется вписанным в сферу (вписанным в шар), если все вершины многогранника принадлежат этой сфере. Про сферу в этом случае говорят, что сфера описана около многогранника.

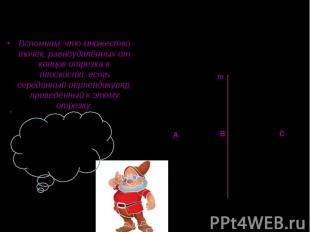
Вспомним, что множество точек, равноудалённых от концов отрезка в плоскости, есть серединный перпендикуляр, проведённый к этому отрезку. Вспомним, что множество точек, равноудалённых от концов отрезка в плоскости, есть серединный перпендикуляр, проведённый к этому отрезку.

Множество точек, равноудалённых от двух данных точек, есть плоскость, перпендикулярная к отрезку с концами в данных точках, проходящих через его середину (плоскость серединных перпендикуляров). Множество точек, равноудалённых от двух данных точек, есть плоскость, перпендикулярная к отрезку с концами в данных точках, проходящих через его середину (плоскость серединных перпендикуляров).

Множество точек, равноудалённых от «n» данных точек («n» больше 2), лежащих на одной окружности, есть прямая, перпендикулярная плоскости этих точек, проходящая через центр описанной около них окружности. Множество точек, равноудалённых от «n» данных точек («n» больше 2), лежащих на одной окружности, есть прямая, перпендикулярная плоскости этих точек, проходящая через центр описанной около них окружности.

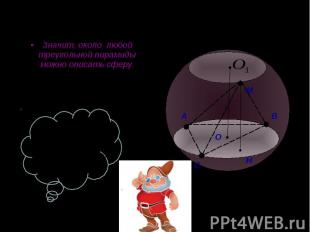
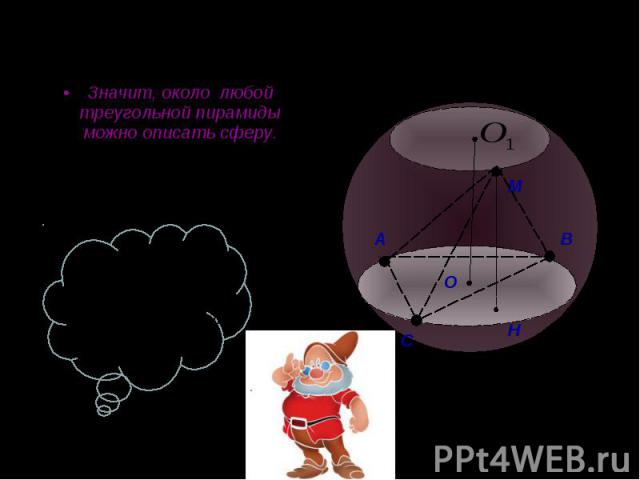
Значит, около любой треугольной пирамиды можно описать сферу. Значит, около любой треугольной пирамиды можно описать сферу.

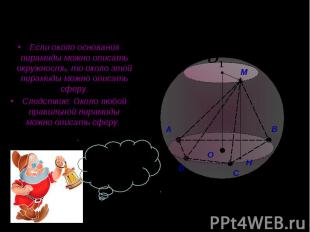
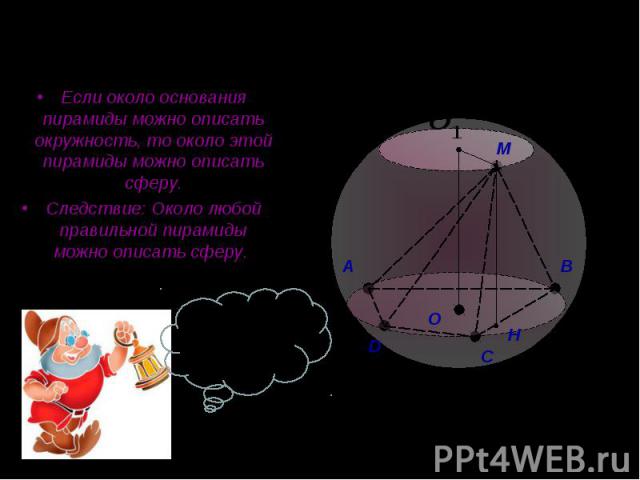
Если около основания пирамиды можно описать окружность, то около этой пирамиды можно описать сферу. Если около основания пирамиды можно описать окружность, то около этой пирамиды можно описать сферу. Следствие: Около любой правильной пирамиды можно описать сферу.

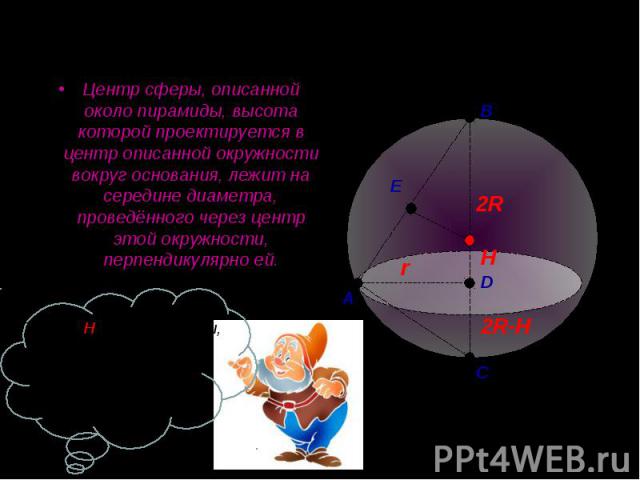
Центр сферы, описанной около пирамиды, высота которой проектируется в центр описанной окружности вокруг основания, лежит на середине диаметра, проведённого через центр этой окружности, перпендикулярно ей. Центр сферы, описанной около пирамиды, высота которой проектируется в центр описанной окружности вокруг основания, лежит на середине диаметра, проведённого через центр этой окружности, перпендикулярно ей.

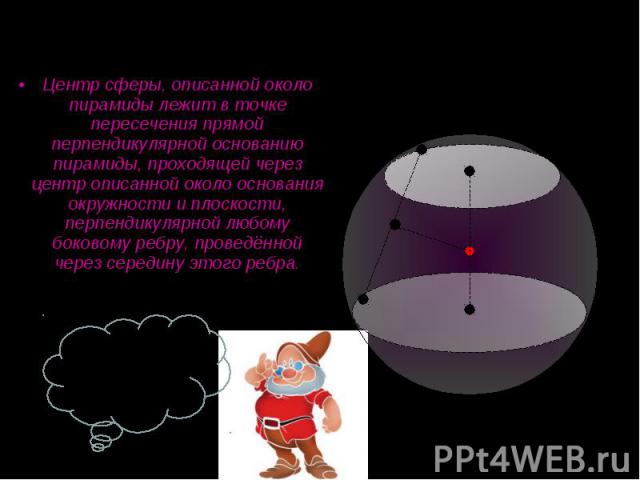
Центр сферы, описанной около пирамиды лежит в точке пересечения прямой перпендикулярной основанию пирамиды, проходящей через центр описанной около основания окружности и плоскости, перпендикулярной любому боковому ребру, проведённой через середину этого ребра. Центр сферы, описанной около пирамиды лежит в точке пересечения прямой перпендикулярной основанию пирамиды, проходящей через центр описанной около основания окружности и плоскости, перпендикулярной любому боковому ребру, проведённой через середину этого ребра.