Презентация на тему: Первообразная

Первообразная Тема Урока:

Содержание урока: F'(x) = f(x) Определение первообразной F(x)+C = ∫f(x)dx Неоднозначность первообразной Нахождение первообразных в простейших случаях Проверка первообразной на заданном промежутке

Устные упражнения а) ( )' = 2x б) ( )' = 0 в) ( )' = г) ( )' = cos x д) ( )' = ex е) ( )' = x +

Взаимно-обратные операции в математике Прямая

Пояснение в сравнении Производная "Производит" новую ф-ию

Определение первообразной

Неоднозначность первообразной

Определение интеграла

Правила интегрирования

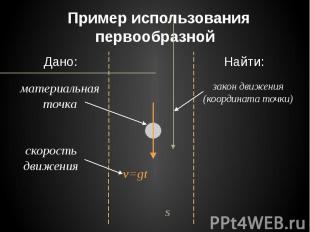
Пример использования первообразной

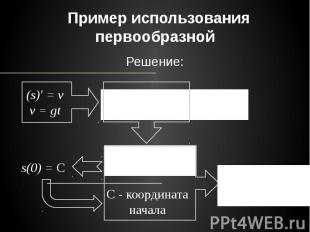
Пример использования первообразной

Отработка материала Практические задания

Найти одну из первообразных для следующих функций 1) f(x) = 4 2) f(x) = -1 3) f(x) = x3 4) f(x) = sin x 5) f(x) = x2 + 3cos x

Док-ть, что F(x) первообразная для f(x) на заданном промежутке Условия Дано: F(x) = 3x4 Док-ть: f(x) = 12x3 при x ∈ (-∞;+∞)

Задачи на доказательство: 1) F(x) = ; f(x) = ; x ∈ [0;+∞) 2) F(x) = 2(sin2x) - 3; f(x) = 4cos2x; x ∈ (-∞;+∞) 3) F(x) = ln(-x); f(x) = ; x ∈ (-∞;0) 4) F(x) = ln x; f(x) = ; x ∈ (0;+∞)

Домашнее задание Теория: §20, определение наизусть Практика: № 20.1 № 20.4 (в,г) № 20.5 (в,г)