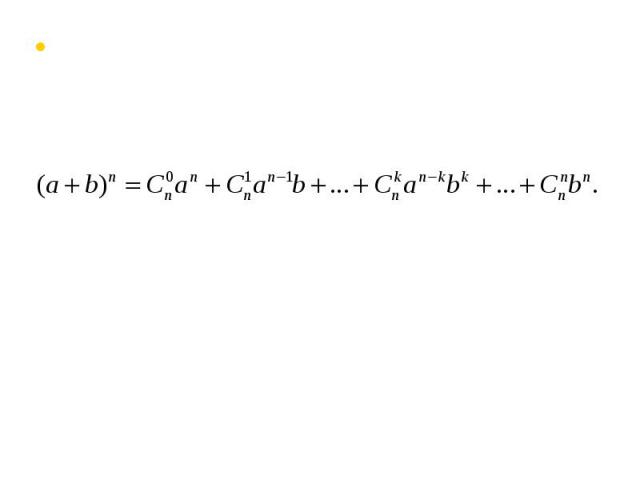Презентация на тему: Основы комбинаторики

§ 1. Примеры комбинаторных задач и общие принципы комбинаторики

Правило произведения Правило произведения Пусть объект а1 можно выбрать n1, различными способами, после каждого выбора объекта а1 объект а2 можно выбрать n2 различными способами,..., после каждого выбора объектов а1, а2,..., аp-1 объект аp можно выбрать nр различными способами. Тогда количество способов, которыми можно выбрать а1, а2, ..., аp равно n1n2...np.

Составление слова из восьми букв можно представить как заполнение буквами клеток следующей таблицы: Составление слова из восьми букв можно представить как заполнение буквами клеток следующей таблицы: 1 2 3 4 5 6 7 8 На первое место можно поставить любую из восьми букв, на второе - любую из семи оставшихся и т.д. вплоть до заполнения единственным способом клетки № 8 последней оставшейся буквой. Число способов заполнения таблицы будет равно 8·7·6·5·4·3·2·1=8! Напомним, что символом п! (читается «эн факториал») обозначается произведение всех натуральных чисел от 1 до п: n!=1·2·...·(n-1)·n. Ответ: n!= 1 • 2 • ...• (n -1) • п.

Пример 2. Сколько четырехбуквенных «слов» можно составить из карточек «в», «е», «ч», «н», «о», «с», «т», «ь»? Пример 2. Сколько четырехбуквенных «слов» можно составить из карточек «в», «е», «ч», «н», «о», «с», «т», «ь»?

Пример 3. Сколькими способами можно поставить на шахматную доску белую и черную ладью так, чтобы они не били друг друга? Пример 3. Сколькими способами можно поставить на шахматную доску белую и черную ладью так, чтобы они не били друг друга?

Выбор объекта а1 - поля для белой ладьи - может быть сделан n1 = 64 способами. Независимо от выбора этого поля белая ладья бьет 15 полей, поэтому для черной ладьи остается 64-15 =49 полей: n2 = 49. Выбор объекта а1 - поля для белой ладьи - может быть сделан n1 = 64 способами. Независимо от выбора этого поля белая ладья бьет 15 полей, поэтому для черной ладьи остается 64-15 =49 полей: n2 = 49. Ответ: число расстановок ладей равно 64 · 49 = 3136.

Пример 5. Сколь различных слов можно получить, переставляя буквы слова «комбинаторика»? Пример 5. Сколь различных слов можно получить, переставляя буквы слова «комбинаторика»?

В слове «комбинаторика» 13 букв. Если бы все они были различны, то, переставляя их, можно было бы получить 13! слов. Но в нашем слове буквы к, о, и, а встречаются по два раза. Обозначим их к1,к2,о1,о2,и1,и2,а1,а2. Ясно, что слова, отличающиеся перестановкой букв к1ик2 - одинаковые, так что 13! Слов разбиваются на пары одинаковых. Следовательно, если мы не различаем к1 и к2, то число всех слов будет равно 13!/2!. Но эта совокупность также разбивается на пары одинаковых с точки зрения буквы “о„ слов и т.д. В слове «комбинаторика» 13 букв. Если бы все они были различны, то, переставляя их, можно было бы получить 13! слов. Но в нашем слове буквы к, о, и, а встречаются по два раза. Обозначим их к1,к2,о1,о2,и1,и2,а1,а2. Ясно, что слова, отличающиеся перестановкой букв к1ик2 - одинаковые, так что 13! Слов разбиваются на пары одинаковых. Следовательно, если мы не различаем к1 и к2, то число всех слов будет равно 13!/2!. Но эта совокупность также разбивается на пары одинаковых с точки зрения буквы “о„ слов и т.д. 13! 13! Ответ: = = —. 2!2!2!2! 16

Пример 6. Сколько существует четырехзначных чисел, у которых все цифры нечетные? Сколько существует четырехзначных чисел, в записи которых есть хотя бы одна четная цифра? Пример 6. Сколько существует четырехзначных чисел, у которых все цифры нечетные? Сколько существует четырехзначных чисел, в записи которых есть хотя бы одна четная цифра?

Всего нечетных цифр — пять, поэтому выбор к-й цифры числа может быть сделан nк =5 способами (к =1, 2, 3, 4) а количество четырехзначных чисел, у которых все цифры нечетные, равно 5·5·5·5 = 625. Всего нечетных цифр — пять, поэтому выбор к-й цифры числа может быть сделан nк =5 способами (к =1, 2, 3, 4) а количество четырехзначных чисел, у которых все цифры нечетные, равно 5·5·5·5 = 625.

Правило суммы Правило суммы

Пример 7. Сколько различных пар можно образовать из 28 костей домино так, чтобы кости, входящие в пару, можно было приложить друг к другу? Пример 7. Сколько различных пар можно образовать из 28 костей домино так, чтобы кости, входящие в пару, можно было приложить друг к другу?

Выбор пары костей — это выбор двух карточек вида a1b1, a2b2, Выбор пары костей — это выбор двух карточек вида a1b1, a2b2, где можно считать, что а ≤ b. Выберем первую кость - это можно сделать 28 способами, из них в 7 случаях кость окажется дублем, т.е. кость вида aa, а в 21 случае — кость вида ab, а < b . В первом случае вторую кость можно выбрать 6 способами, а число способов выбора пары костей по правилу произведения равно 7 · 6 = 42 . Во втором случае вторую кость можно выбрать 12 способами — 6 костей вида a|* и 6 костей вида *|а ,а число способов выбора пары равно 21·12 = 252. Следовательно по правилу суммы всего получается 42 + 252 = 294 способа выбора упорядоченной пары. Ответ: 147 пар.

§ 2. Размещения и перестановки

Определение. Всякая упорядоченная выборка объема k из множества, состоящего из n элементов, называется размещением из n элементов по k элементов и обозначается через Аn . Определение. Всякая упорядоченная выборка объема k из множества, состоящего из n элементов, называется размещением из n элементов по k элементов и обозначается через Аn .

Определение. Размещение из n элементов по n называется перестановкой из n элементов и обозначается через Рn . Определение. Размещение из n элементов по n называется перестановкой из n элементов и обозначается через Рn .

Справедлива формула Справедлива формула Аn =n (n-1)...(n - к + 1)

На первое место в выборке можно поместить любой из n элементов, на второе - любой из (n - 1) оставшихся и т.д. После выбора элементов на(k-1)-е место останется n-(к-1) = n-к+1 элемен- На первое место в выборке можно поместить любой из n элементов, на второе - любой из (n - 1) оставшихся и т.д. После выбора элементов на(k-1)-е место останется n-(к-1) = n-к+1 элемен- 1 2 k-1 k тов, любой из которых можно поместить на к-е место. По правилу произведения получаем Аn = (n-1)...(n - к + 1) В частности, Рn=An =n(n-1)… ·2·1 = n! (2)

An = n(n - 1)...(n - k+1)·(n-k)!= n! An = n(n - 1)...(n - k+1)·(n-k)!= n! (n-к)! (n-к)!

Пример 9. Сколько шестизначных чисел, кратных 5, можно составить из цифр 0, 1,2, ..., 9 при условии, что цифры в записи числа не повторяются? Пример 9. Сколько шестизначных чисел, кратных 5, можно составить из цифр 0, 1,2, ..., 9 при условии, что цифры в записи числа не повторяются?

Последней цифрой искомого числа может быть 0 или 5. В первом случае остальные пять цифр можно выбирать из множества {1,2, ..., 9} Последней цифрой искомого числа может быть 0 или 5. В первом случае остальные пять цифр можно выбирать из множества {1,2, ..., 9} 9! и число вариантов равно А9 = — = 15120. Если число 4! oканчивается цифрой 5, то в качестве первой цифры можно взять любую из восьми цифр 1, 2, 3, 4, 6, 7, 8, 9 - нельзя использовать 0, т.к. число должно быть шестизначным. Цифры со второй по четвертую можно выбрать A8 = 1680 различными способами. Следовательно, по правилу произведения имеется 8·A8 чисел, оканчивающихся цифрой 5. По правилу суммы находим, сколько существует чисел, удовлетворяющих условию задачи. А9 +8·A8 = 28560. Ответ: 28560.

Пример 10. Сколькими способами можно расставить на книжной полке десятитомник Пушкина так, чтобы том 2 стоял рядом с томом 1 и справа от него? Пример 10. Сколькими способами можно расставить на книжной полке десятитомник Пушкина так, чтобы том 2 стоял рядом с томом 1 и справа от него? Ответ: 9!

§ 3. Сочетания

Определение. Всякая неупорядоченная выборка объема к из множества, состоящего из n элементов (к≤n), называется сочетанием из n элементов по к элементов и обозначается через Сn . Определение. Всякая неупорядоченная выборка объема к из множества, состоящего из n элементов (к≤n), называется сочетанием из n элементов по к элементов и обозначается через Сn .

Из любого набора,содержащего к элементов, можно с помощью перестановок получить k! упорядоченных выборок объема k, поэтому Из любого набора,содержащего к элементов, можно с помощью перестановок получить k! упорядоченных выборок объема k, поэтому Откуда (4)

Пример 11. Хоккейная команда состоит из 2 вратарей, 7 защитников и 10 нападающих. Сколькими способами тренер может образовать стартовую шестерку, состоящую из вратаря, двух защитников и трех нападающих? Пример 11. Хоккейная команда состоит из 2 вратарей, 7 защитников и 10 нападающих. Сколькими способами тренер может образовать стартовую шестерку, состоящую из вратаря, двух защитников и трех нападающих?

Вратаря можно выбрать способами, защитников - Вратаря можно выбрать способами, защитников - способом, нападающих – способами. Всего, по правилу произведения, существует 2 · 21 · 120 = 5040 способов выбора стартовой шестерки. Ответ: 5040.

Пример 12. На плоскости проведены n прямых, среди которых нет ни одной пары параллельных прямых и ни одной тройки прямых, пересекающихся в одной точке. Найти число точек пересечения этих прямых и число треугольников, образованных этими прямыми. Пример 12. На плоскости проведены n прямых, среди которых нет ни одной пары параллельных прямых и ни одной тройки прямых, пересекающихся в одной точке. Найти число точек пересечения этих прямых и число треугольников, образованных этими прямыми.

Число точек пересечения прямых равно числу способов выбора Число точек пересечения прямых равно числу способов выбора неупорядоченной пары прямых, т.е. . Аналогично, каждый треугольник определяется тройкой прямых, поэтому общее число треугольников равно . Ответ: и .

Пример 13. Для проведения письменного экзамена по комбинаторике надо составить 4 варианта по 7 задач в каждом. Сколькими способами можно разбить 28 задач на 4 варианта? Пример 13. Для проведения письменного экзамена по комбинаторике надо составить 4 варианта по 7 задач в каждом. Сколькими способами можно разбить 28 задач на 4 варианта?

Задачи для первого варианта можно выбрать способами. После этого останется 21 задача, так что второй вариант можно составить способами. Для третьего варианта задачи можно выбрать способами, а для четвертого - = 1 способом. Задачи для первого варианта можно выбрать способами. После этого останется 21 задача, так что второй вариант можно составить способами. Для третьего варианта задачи можно выбрать способами, а для четвертого - = 1 способом.

По правилу произведения получаем число . Но так как варианты равноправны, то полученное число надо разделить на 4! По правилу произведения получаем число . Но так как варианты равноправны, то полученное число надо разделить на 4! Ответ: =

Свойства чисел : Свойства чисел : 1°. , если 0≤к≤n; 2°. , если 0≤к≤n+1; 3°.

Свойство 1° Свойство 1°

Свойство 2° Свойство 2°

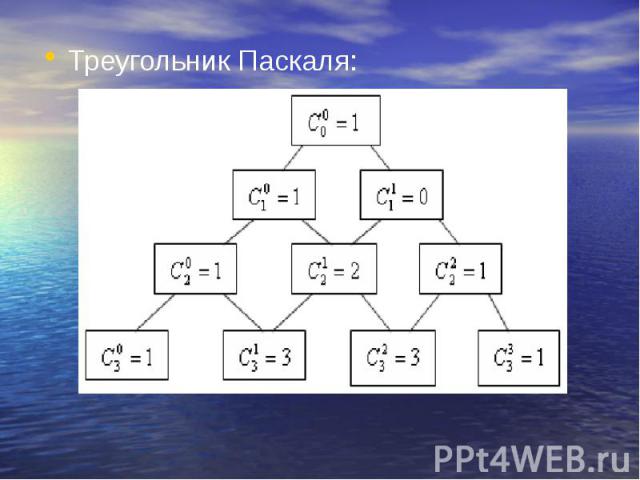
Треугольник Паскаля: Треугольник Паскаля:

Свойство 3° Свойство 3° Положим Так как каждое число строки с номером п входит в качестве слагаемого в два соседних числа следующей строки, то Sn+1 = 2Sn . Следовательно, т.к. S0=1.

§ 4. Бином Ньютона

(a + b) =a +2ab + b и (a + b) = а +3а b + 3ab +b . (a + b) =a +2ab + b и (a + b) = а +3а b + 3ab +b .

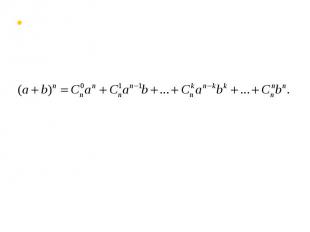
Если в формуле (5) взять а =b = 1, то получится известное нам свойство 3° чисел , а если взять а=1, b = -1, то получим еще одно комбинаторное равенство: Если в формуле (5) взять а =b = 1, то получится известное нам свойство 3° чисел , а если взять а=1, b = -1, то получим еще одно комбинаторное равенство:

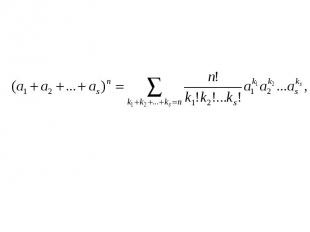
Формула (6) называется полиномиальной. Например, Формула (6) называется полиномиальной. Например, (а + b + с) = а + b + с + 3(а b + а с + b а + b с + с а + c b ) + 6abc.

Пример 14. Найти n, если известно, что в разложении (1 + x) Пример 14. Найти n, если известно, что в разложении (1 + x) коэффициенты при х и х равны.

В n-й строке треугольника Паскаля два коэффициента равны в том и только том случае, когда они занимают клетки, равноудаленные от крайних. Действительно, треугольник Паскаля симметричен: , а при движении от края к середине строки коэффициенты возрастают: при В n-й строке треугольника Паскаля два коэффициента равны в том и только том случае, когда они занимают клетки, равноудаленные от крайних. Действительно, треугольник Паскаля симметричен: , а при движении от края к середине строки коэффициенты возрастают: при и при

Следовательно, равно тогда и только тогда, когда 12 = n-5, т.е. n= 17. Следовательно, равно тогда и только тогда, когда 12 = n-5, т.е. n= 17. Ответ: n = 17.

Пример 15. Найти коэффициент при х в разложении Пример 15. Найти коэффициент при х в разложении (1 + х +х ) .

В силу формулы (6) В силу формулы (6) = Так как уравнение 5k2 + 9к3 =19 имеет только одно решение в неотрицательных числах k2=2, k3 = 1, то коэффициент при х равен

2) Обозначим через . Тогда 2) Обозначим через . Тогда Рассмотрим k-е слагаемое (0≤k≤30): Такое слагаемое будет содержать х , если для некоторого т выполняется равенство 5k + 4m = 19. Ясно, что это возможно только при k=3 и т=1. Следовательно, коэффициент при х равен =12180.

Литература Литература 1. Кутасова А.Д., Пиголкина Т.С, Чехлов В.И., Яковлева Т.Х., Пособие по математике для поступающих в вузы. /под ред. Г.Н. Яковлева - M.: Наука, 1988. 2. Виленкин Н.Я. Популярная комбинаторика. — М.: Наука, 1975. 3. Генкин С.А., Итенберг И.В., Фомин Д.В. Ленинградские математические кружки. — Киров, 1994.

Контрольные вопросы Контрольные вопросы Сколько делителей у числа 2004 ? Сколько диагоналей в выпуклом 2004-угольнике? Сколько различных натуральных решений имеет неравенство n+m≤2004? 4. Чему равен коэффициент при х y в выражении (х + у) после раскрытия скобок? 5. С помощью соответствующей строки треугольника Паскаля выпишите формулу для вычисления (а-b) .

Задачи Задачи 1(3). Сколько различных слов можно получить, переставляя буквы в слове «параллелограмм»? 2(4). Сколькими способами можно переставлять буквы слова «раз-­ мещение» так, чтобы три буквы «е» не шли подряд? 3(3). Решите уравнение 4(3). Известно, что никакие три диагонали выпуклого восьмиуголь­ника не пересекаются в одной точке. Найдите число точек пе­ресечения диагоналей. 5(4). Сколькими способами можно поставить на шахматную доску белого и черного слонов так, чтобы они не били друг друга? 6(5). Найдите сумму всех трехзначных чисел, которые можно напи­сать с помощью цифр 1, 2, 3, 4, 5 (любую из цифр можно ис­пользовать несколько раз). 7(5). Докажите тождество 8(6).Сколькими способами можно распределить 12 различных книг по четырем полкам так, чтобы на каждой полке ока­залась ровно три книги? 9(6). Сколькими способами можно распределить 12 одинако­вых книг по четырем полкам так, чтобы на каждой полке была хотя бы одна книга? В задачах №8 и №9 все полки разные. 10(6). В выпуклом восьмиугольнике проведены все диагона­ли, причем известно, что никакие три диагонали не пере­секаются в одной точке. На сколько частей разделится восьмиугольник? 11(6). Найдите наибольший коэффициент многочлена (1 + 2х) . 12(6). Найдите коэффициент при х в разложении по степе ням х 1+(1+x)+…+(1+x) .