Презентация на тему: Дроби в 4 классе

Дроби в 4 классе Действия над ними

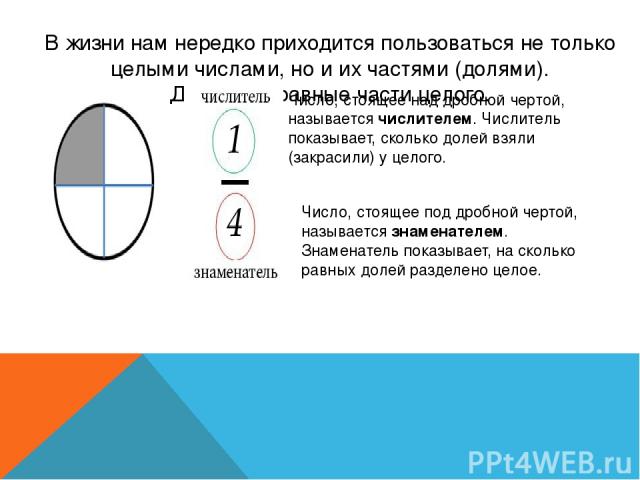
В жизни нам нередко приходится пользоваться не только целыми числами, но и их частями (долями). Доли - это равные части целого. Число, стоящее над дробной чертой, называется числителем. Числитель показывает, сколько долей взяли (закрасили) у целого. Число, стоящее под дробной чертой, называется знаменателем. Знаменатель показывает, на сколько равных долей разделено целое.

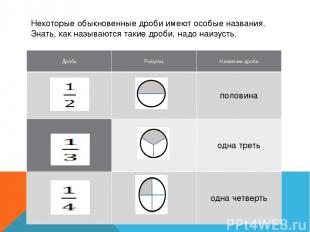
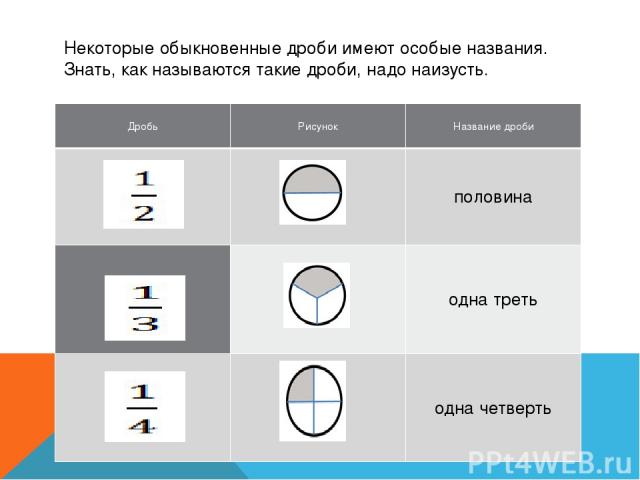
Некоторые обыкновенные дроби имеют особые названия. Знать, как называются такие дроби, надо наизусть. Дробь Рисунок Название дроби половина одна треть одна четверть

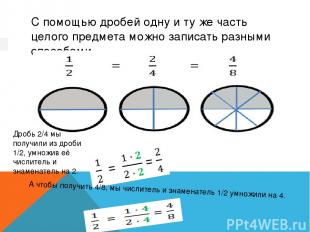
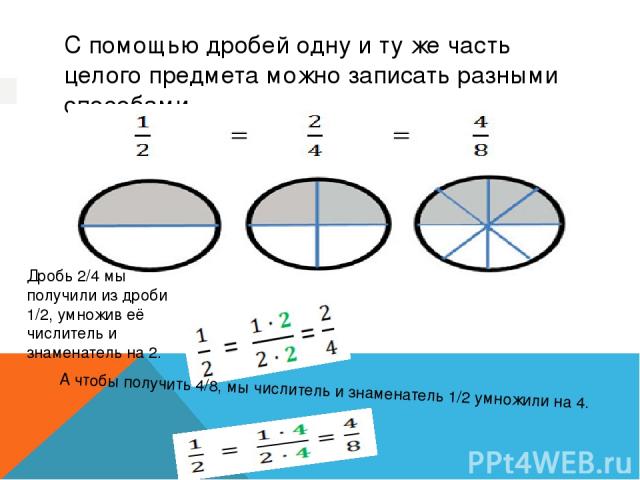
С помощью дробей одну и ту же часть целого предмета можно записать разными способами. А чтобы получить 4/8, мы числитель и знаменатель 1/2 умножили на 4. Дробь 2/4 мы получили из дроби 1/2, умножив её числитель и знаменатель на 2.

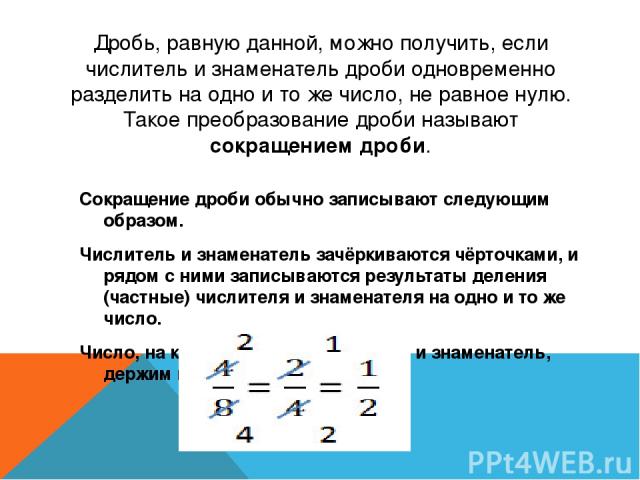
Дробь, равную данной, можно получить, если числитель и знаменатель дроби одновременно разделить на одно и то же число, не равное нулю. Такое преобразование дроби называют сокращением дроби. Сокращение дроби обычно записывают следующим образом. Числитель и знаменатель зачёркиваются чёрточками, и рядом с ними записываются результаты деления (частные) числителя и знаменателя на одно и то же число. Число, на которое делили числитель и знаменатель, держим в уме.

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то получится дробь, равная данной. Запишем это свойство в виде буквенных выражений. ,где a, b и k - натуральные числа.

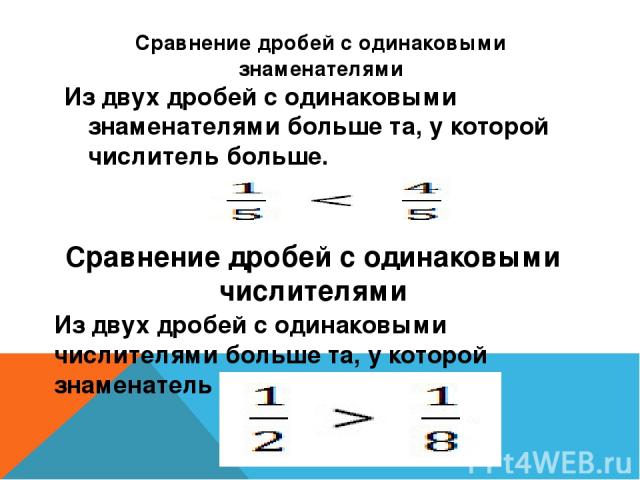
Сравнение дробей с одинаковыми знаменателями Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше. Сравнение дробей с одинаковыми числителями Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.

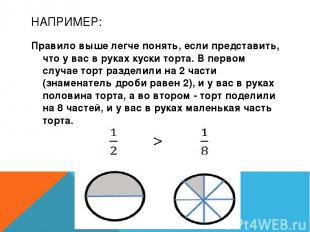
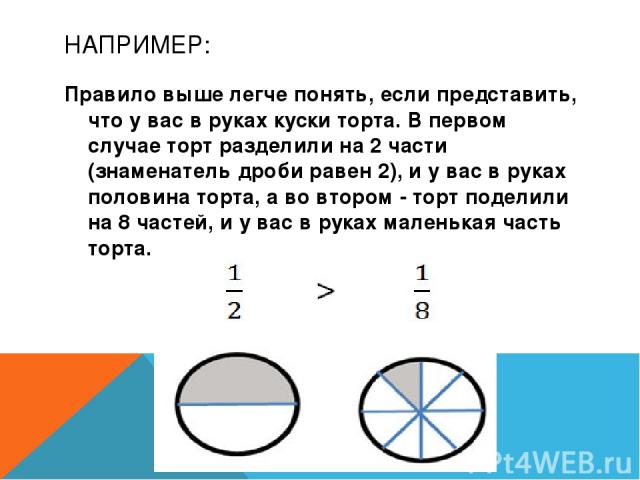
НАПРИМЕР: Правило выше легче понять, если представить, что у вас в руках куски торта. В первом случае торт разделили на 2 части (знаменатель дроби равен 2), и у вас в руках половина торта, а во втором - торт поделили на 8 частей, и у вас в руках маленькая часть торта.

Сложение дробей с одинаковыми знаменателями Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают числители, а знаменатель оставляют тот же. Пример. Вычитание дробей с одинаковыми знаменателями При вычитании дробей с одинаковыми знаменателями от числителя уменьшаемого (первой дроби) отнимают числитель вычитаемого (второй дроби), а знаменатель оставляют прежним. Пример.

Вычитание правильной дроби из единицы Когда нужно вычесть из единицы правильную дробь, единицу представляют в виде неправильной дроби, знаменатель которой, равен знаменателю вычитаемой дроби. Пример. Знаменатель вычитаемой дроби равен 7, значит, единицу представляют как неправильную дробь 7/7 и вычитают по правилу вычитания дробей с одинаковыми знаменателями.

Зная целое, можно найти его часть, указанную соответствующей дробью. Чтобы найти дробь (часть) от числа, нужно это число умножить на данную дробь Пример. Рассмотрим задачу. В книге 160 страниц. Юра прочитал 4/5 книги. Сколько страниц прочитал Юра? Прежде всего найдём в задаче целое. Это - вся книга и в ней всего 160 страниц. Посмотрим на дробь (часть) от целого: 4/5. Знаменатель равен 5, значит, целое разделили на 5 частей и мы можем найти сколько страниц составляет 1/5 часть. Оба действия можно записать кратко, в соответствии с правилом нахождения части от целого.

Если известно сколько составляет часть от целого, то по известной части можно "восстановить" целое. Чтобы найти число по его части, выраженной дробью, нужно данное число разделить на дробь. Пример. Рассмотрим задачу. Поезд прошёл 240 км, что составило 15/23 всего пути. Какой путь должен пройти поезд? Решение. 240 км - часть всего пути. Эти же километры выражены дробью 15/23 от всего пути. Знаменатель дроби говорит о том, что весь путь разделён на 23 части, и 15 таких частей составляют 240 км (числитель дроби равен 15). Значит, можно найти, сколько составляет 1/23 часть пути. 240 : 15 = 16 (км). Весь путь (целое) всегда обозначаем за единицу, которую можно выразить дробью 23/23. Значит, чтобы найти весь путь (23 части, каждая из которых по 16 км) нужно: 16 • 23 = 368 (км) Кратко запись решения такой задачи можно сделать следующим образом.

ДЕЛЕНИЕ МЕНЬШЕГО ЧИСЛА НА БОЛЬШЕЕ Математическую операцию деление вы уже знаете хорошо. До сих пор мы делили большее число на меньшее, а можно ли меньшее число разделить на большее. Рассмотрим пример из жизни. 

ПРИ ДЕЛЕНИИ МЕНЬШЕГО НАТУРАЛЬНОГО ЧИСЛА НА БОЛЬШЕЕ, МЫ ПОЛУЧАЕМ ДРОБЬ, ГДЕ В ЧИСЛИТЕЛЕ ЗАПИСАНО ДЕЛИМОЕ, А В ЗНАМЕНАТЕЛЕ ДЕЛИТЕЛЬ

СПАСИБО ЗА ВНИМАНИЕ