Презентация на тему: Анализ количественных признаков

Анализ количественных признаков

Чем мы занимались на предыдущем занятии

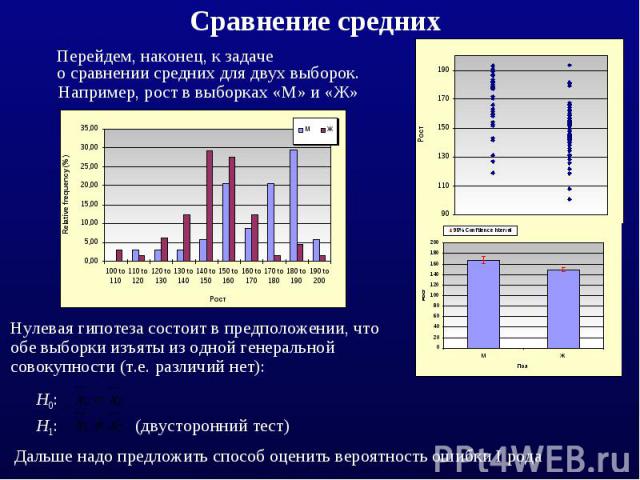
Перейдем, наконец, к задаче о сравнении средних для двух выборок.

прошлом занятии мы рассмотрели достаточно универсальный способ построения статистических критериев: Z – статистика, т.е.

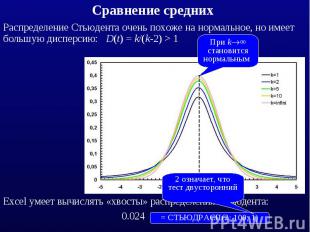
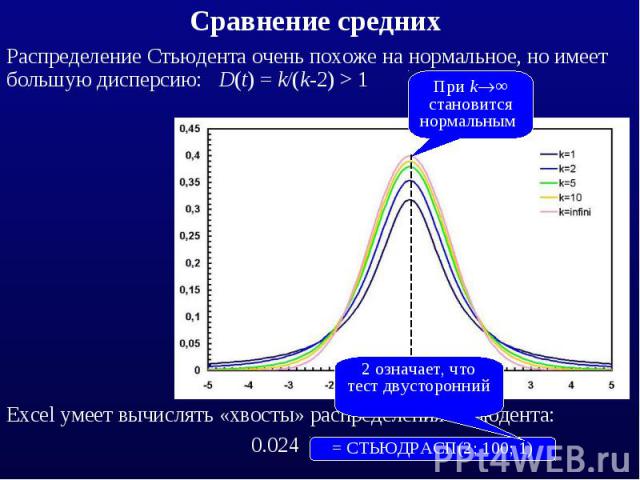
Распределение Стьюдента очень похоже на нормальное, но имеет большую дисперсию: D(t) = k/(k-2) > 1

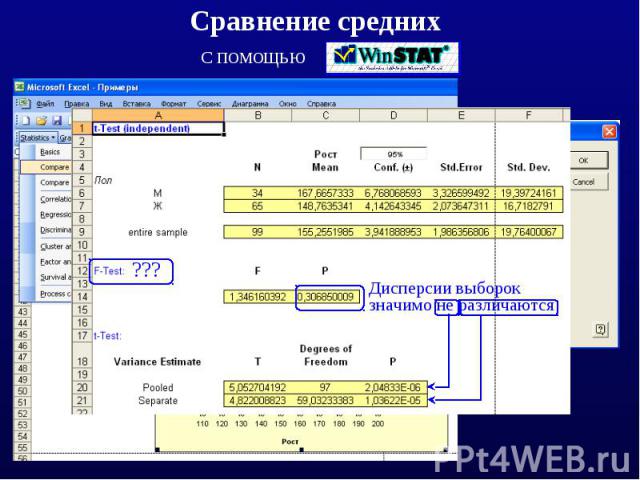
Сравнение средних

Вывод: нулевая гипотеза отвергается. Вероятность того, что при этом отвергли правильную нулевую гипотезу равна 0.022 (ошибка I рода). Выборка по данным районного морга не соответствует среднему по стране. Различия статистически значимы.

Сравнение средних

Сравнение средних

Сравнение средних

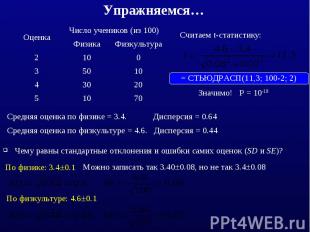
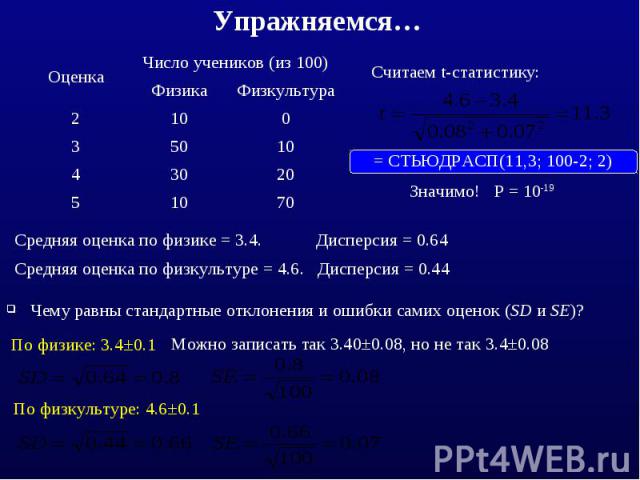
Упражняемся…

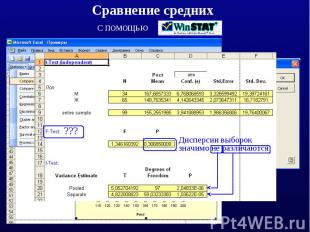
Сравнение средних

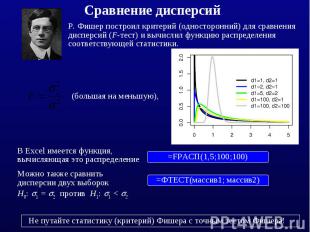
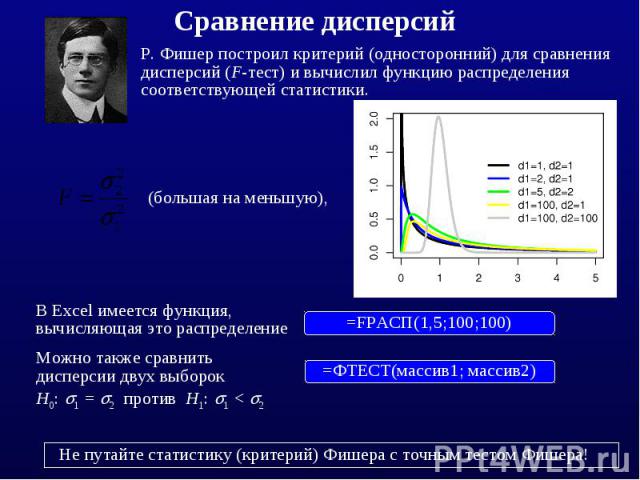
Фишер построил критерий (односторонний) для сравнения дисперсий (F-тест) и вычислил функцию распределения соответствующей статистики.

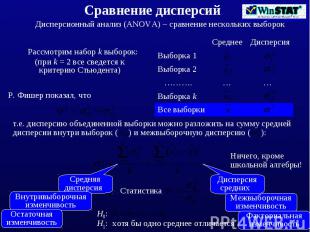
Сравнение дисперсий

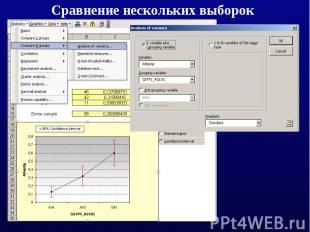
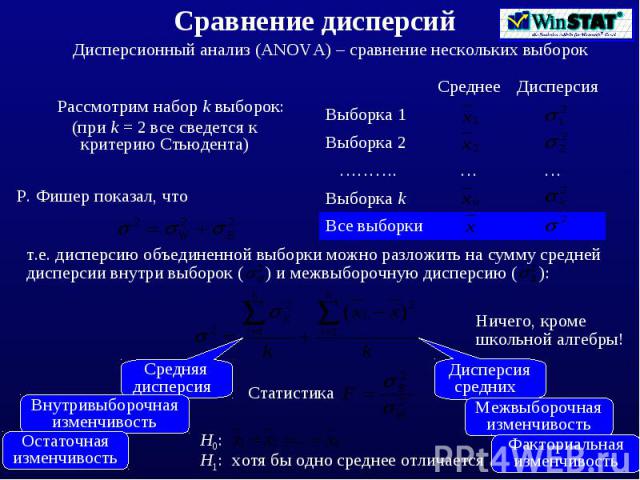
Сравнение нескольких выборок

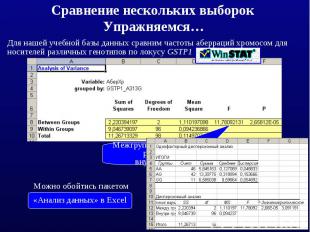
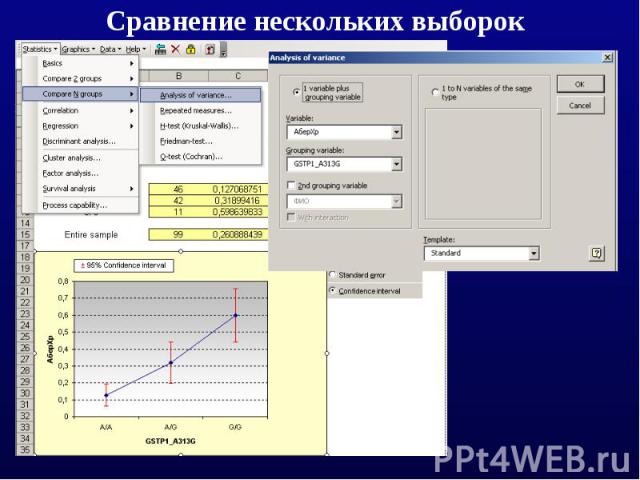
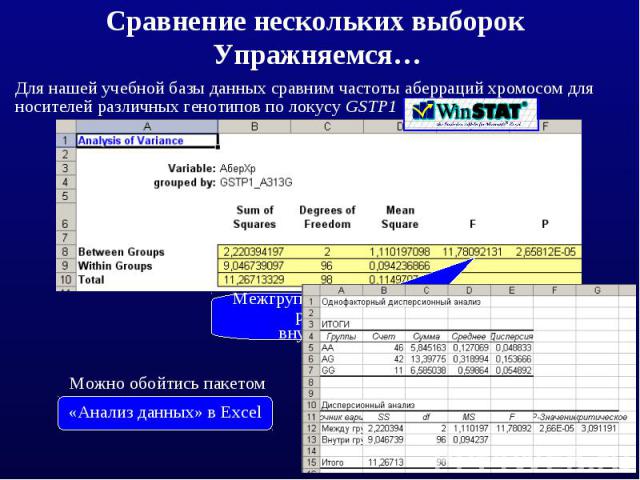
Сравнение нескольких выборок

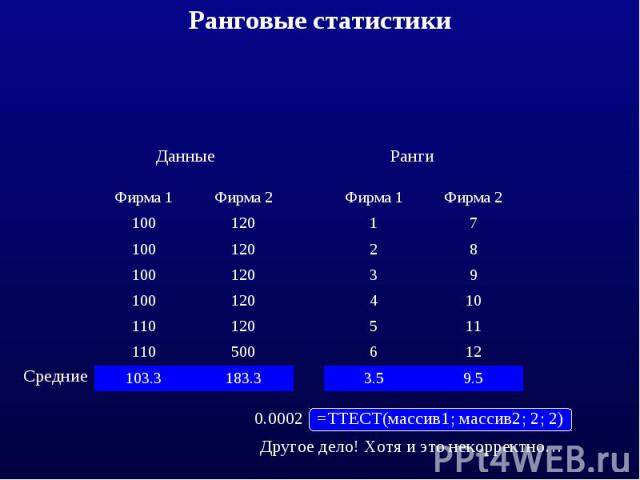
этом примере видно, что в ряде случаев надо сравнивать не сами данные, а их порядковые ранги (номера в последовательности)

этом примере видно, что в ряде случаев надо сравнивать не сами данные, а их порядковые ранги (номера в последовательности)

Ранговые критерии являются непараметрическими, т.е. такими, которые не зависят от характера распределения данных. В частности они нечувствительны к выбросам отдельных точек

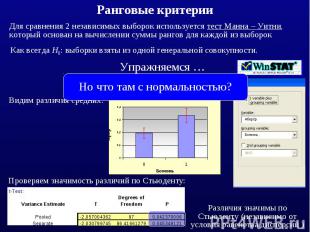
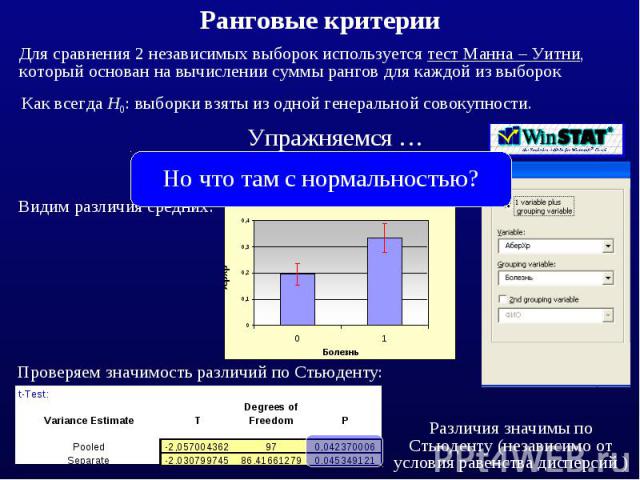
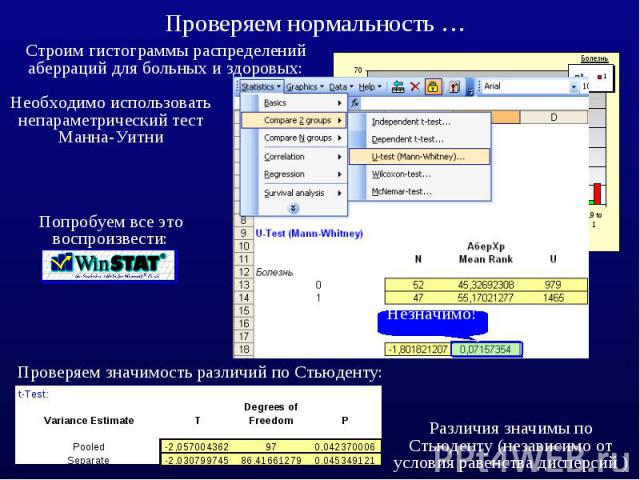
Для сравнения 2 независимых выборок используется тест Манна – Уитни, который основан на вычислении суммы рангов для каждой из выборок

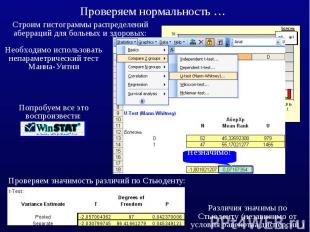
Допустим мы не обнаружили статистическую значимость различий, о чем с грустью сообщаем в публикации. Достаточно ли этого?

Допустим мы не обнаружили статистическую значимость различий, о чем с грустью сообщаем в публикации. Достаточно ли этого?