Презентация на тему: Леонард Эйлер для 6 классов

Леонард Эйлер: жизнь, творчество, служение России Выполнила Данькова Валентина Николаевна

Л. Эйлер (1707 – 1783)

Важнейшие даты жизни и деятельности 4 апреля 1707 г. – в Базеле (Швейцария) в семье пастора родился Л. Эйлер 1720 г. – студент младшего философского факультета Базельского университета 9 июня 1722 г. – получил степень «Первые лавры» (бакалавр) по философии 1723 г. – поступил на богословский факультет (по настоянию отца) 8 июня 1724 г. – получил степень магистра искусств (за речь о сравнении философских воззрений Ньютона и Декарта)

24 мая 1727 г. – адъюнкт Петербургской А.Н. по математике 24 мая 1727 г. – адъюнкт Петербургской А.Н. по математике 1731 г. – занимает кафедру теоретической и экспериментальной физики 1733 г. – академик Петербургской А.Н. по математике 1733 г. – женитьба на дочери живописца Екатерине Гзелль 1735 г. – работа в Географическом департаменте 1741-1766 гг. – работа в Берлинской А.Н. 1766 г. – возвращение в Петербургскую А.Н. 18 сентября 1783 г. – смерть Л.Эйлера от кровоизлияния в мозг

Главнейшие труды Л. Эйлера 1. Введение в арифметику (1738—1740, немецк., два тома, Спб.). 2. Введение в алгебру (1770, немецк., Спб.). 3. Введение в анализ бесконечно малых (1748, латынь, два тома, Лозанна). 4. Дифференциальное исчисление (1755, латынь, Бер­лин). 5. Интегральное исчисление (1768—1770, латынь, три тома, Спб.). 6. Метод нахождения кривых линий, обладающих свойствами максимума или минимума (1744, латынь, Ло­занна). 7. Механика в аналитическом изложении (1736, ла­тынь, два тома, Спб.). 8. Теория движения твердых тел (1765, латынь, Ро­сток).

9. Механика жидких тел (наиболее важный мемуар относится к 1769, латынь, Спб.). 9. Механика жидких тел (наиболее важный мемуар относится к 1769, латынь, Спб.). 10. Сопротивление колонн (1757, франц., Берлин). 11. Новые начала артиллерии Робинса, переведенные с английского и снабженные необходимыми объяснения­ми и многими примечаниями (1745, немецк., Берлин). 12. Теория движения планет и комет (1744, латынь, Берлин). 13. Теория движения Луны (1753, латынь, Берлин) 14. Теория движения Луны, пересмотренная новым методом (1772, латынь, Спб.) 15. Теория приливов и отливов (1740, латынь, Париж). 16. Устройство объективов из двух стекол (ахромати­ческих, латынь, 1762, Спб.).

17. Диоптрика (1769—1771, латынь, три тома, Спб.). 17. Диоптрика (1769—1771, латынь, три тома, Спб.). 18. Теория музыки (1739, латынь, Спб.). 19. Диссертация о магните (1743—1744, латынь, Париж). 20. Морская наука (1749, латынь, Спб.) 21. Полная теория конструкции и вождения кораблей (1773, франц., Спб.). 22. Письма к одной немецкой принцессе о разных пред­метах физики и философии (1768—1772, франц., три тома, Спб.).

Основные достижения Эйлера Значение Эйлера для развития математики, механики и многих других наук очень велико, его работы, прокладывающие новые творческие пути, многочисленны. В настоящее время известно 865 его сочинений, из них отдельных многостраничных сочинений – 43 тома. Внес вклад в такие математические дисциплины как вариационное исчисление, интегрирование обыкновенных дифференциальных уравнений, степенные ряды, специальные функции, дифференциальная геометрия, теория чисел; Ввел двойные интегралы, преобразовал тригонометрию, придав ей практически современный вид, уделял большое внимание прикладным вопросам математики;

Заложил основы математической физики, механики твердого тела, гидродинамики, гидравлики, во многом – механики машин; Заложил основы математической физики, механики твердого тела, гидродинамики, гидравлики, во многом – механики машин; Опубликовал серию работ по астрономии, систематически изложил теорию упругих кривых, получил важные результаты по сопротивлению материалов, активно занимался навигацией, баллистикой, диоптрикой; Создал основные руководства для университетов по высшей математике, написал учебники арифметики и алгебры для гимназии, высказал основополагающие идеи развития школьного математического образования…

Эйлер сообщил математическому образованию содержательный и методический заряд, который очень быстро по историческим меркам приблизил отечественное математическое образование к европейскому качественному уровню. В России он создал и оперативно включил в действие механизм патронажа математики как науки над математическим образованием. Эта тенденция нашла свое воплощение в уникальном явлении отечественной истории – методической школе Л. Эйлера, которая обеспечила оперативный доступ к педагогическим и методическим идеям Европы; обогатила и переосмыслила их; сделала приоритетным создание оригинальной отечественной математической литературы, а не переводной западной. Эйлер сообщил математическому образованию содержательный и методический заряд, который очень быстро по историческим меркам приблизил отечественное математическое образование к европейскому качественному уровню. В России он создал и оперативно включил в действие механизм патронажа математики как науки над математическим образованием. Эта тенденция нашла свое воплощение в уникальном явлении отечественной истории – методической школе Л. Эйлера, которая обеспечила оперативный доступ к педагогическим и методическим идеям Европы; обогатила и переосмыслила их; сделала приоритетным создание оригинальной отечественной математической литературы, а не переводной западной.

Методические идеи Эйлера идея сближения содержания математического образования с современной математикой; идея вычленения в школьном математическом образовании основ математических дисциплин – арифметики, геометрии, тригонометрии, впоследствии алгебры; идея построения математических курсов на основе дидактических принципов как систематичность, научность, доступность изложения математических дисциплин, учет возрастных особенностей учащихся.

Некоторые знаменитые математические факты, носящие имя Эйлера Теорема Эйлера о треугольнике; Теорема Эйлера о многогранниках; Функция Эйлера; Формулы Эйлера; Интегралы Эйлера; Задача Эйлера о семи мостах; Задача Эйлера о ходе конем.

Теорема Эйлера : Середины сторон треугольника, основания его высот и середины отрезков высот треугольника от ортоцентра до вершины лежат на одной окружности;

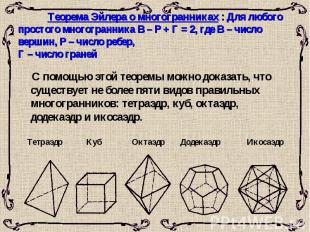
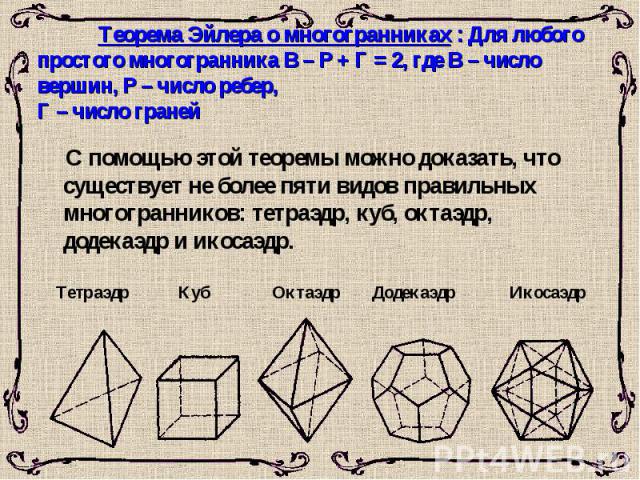
Теорема Эйлера о многогранниках : Для любого простого многогранника В – Р + Г = 2, где В – число вершин, Р – число ребер, Г – число граней С помощью этой теоремы можно доказать, что существует не более пяти видов правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр и икосаэдр. Тетраэдр Куб Октаэдр Додекаэдр Икосаэдр

Функция Эйлера Продолжая работы Ферма по теории чисел Эйлер ввел функцию φ(m), которая называется функцией Эйлера – количество натуральных чисел, меньших данного m и взаимно простых с ним. Так же Эйлер обобщил малую теорему Ферма и доказал, что если а и m взаимно простые числа, то а φ(m) – 1 делится на m. Это предложение называется теоремой Эйлера (о сравнениях).

Формулы Эйлера Занимаясь научной деятельностью Эйлер заметил, что разложения в ряд показательных и тригонометрических функций почти совпадают – и вывел знаменитые формулы Эйлера: e ix = cosx + sinx Полагая, что х = π, получим: e iπ = cos π + sin π = -1

Интегралы Эйлера Пытаясь найти формулу для общего выражения суммы гипергеометрического ряда 1 + 1 2 + 1 2 3 + …+ 1 2 …к + … Эйлер пришел к интегралам, которые впоследствии получили название эйлеровы интегралы, а позднее – бета-функцией Эйлера и гамма-функцией Эйлера:

Задача Эйлера о семи мостах В задаче решается вопрос : как можно пройти по семи кенигсбергским мостам через реку Прегль, пройдя по каждому мосту не более одного раза? На «ордене Семи Мостов» темные места представляют собой речку, а белые – берега речки и мосты. Эйлер доказал, что сделать это невозможно, и нашел общие правила, которым подчиняются задачи такого типа.

Задача Эйлера о ходе конем В задаче решается вопрос : Как разместить в 64 клетках шахматной доски 64 числа от 1 до 64 так, чтобы любые две клетки, в которых содержатся два последовательных числа, были связаны ходом коня? Эйлер первым разработал методы решения этой задачи.

Репродукция титульного листа «Комментариев» в которых печатались работы Эйлера

Эйлер похоронен в С.-Петербургском некрополе – Александро-Невкой лавре. Надпись на памятнике гласила : «Леонарду Эйлеру – Петербургская Академия». Эйлер похоронен в С.-Петербургском некрополе – Александро-Невкой лавре. Надпись на памятнике гласила : «Леонарду Эйлеру – Петербургская Академия». Без сомнения, имя Леонарда Эйлера является одним из самых славных в плеяде выдающихся математиков всех времен, его труды и сейчас продолжают оказывать решающее влияние на прогресс всей современной математики.

Спасибо за внимание!!!