Презентация на тему: Функия у= модуль х

Функция y = |x| Скадорова Альбина, 9 «В».

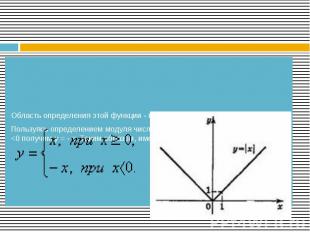
Область определения этой функции - множество R  действитель­ных чисел. Пользуясь определением модуля числа х при х > О получим у = х, а при х <0 получим у = - х. Таким образом, имеем:

Свойства функции 1.  Если х = 0, то у = 0, т.е. график пересекает оси координат в точке (0; 0) - начале координат. 2.  Если х ≠ 0, то у > 0, т.е. все точки графика   функции  y = |x|,   кроме   начала координат, лежат над осью абсцисс. 3.   Множеством значений функции y = |x|  является промежуток [0;+∞). 4. Если значения аргумента отличаются только знаком, то значения функции равны, т.е. график функции симметричен относительно ординат (функция y = |x| - четная). 5.  На промежутке [0;+∞) функция y = |x|  возрастает. 6. На промежутке (-∞;0] функция y = |x|  убывает. 7.  Наименьшее значение функция принимает в точке х, оно равно 0. Наибольшего значения не существует.