Презентация на тему: Современные проблемы информатики

Современные проблемы информатикиЛекция 2Алгебра поведений

Что такое поведение? (инвариант бисимуляционной эквивалентности) В теории автоматов: Автомат есть транзиционная система, размеченная парами вход/выход Поведение есть автоматное отображениеИли Автомат есть настроенная транзиционная система, размеченная входными символами Поведение есть язык 1.Domain theory approach (S.Abramsky 1991)2.ACP with recursion (J.A.Bergstra and J.W.Klop, 1984)3.Coalgebraic approach (P.Aczel, 1988, later B.Jecobs and J.Rutten) 4.Continuous algebras (A.Letichevsky,D.Gilbert,1997)

Алгебра поведений Два сорта: <U, A>U – поведенияA – действияСигнатура:префиксинг a.uнедетерминированный выбор u + vконстанты D, 0, ^отношение аппроксимацииАксиомы:аci для недетерминированного выбора0 есть нейтральный элемент недетерминированного выбора есть отношение частичного порядка с наименьшим элементом ^Обе операции монотонны и непрерывны (сохраняют наименьшие верхние грани) Дополнительные структуры: Действия: комбинация действий ´ , невозможное и нейтральное действия Атрибуты: функции на поведениях

Монотонность

Непрерывность Направленное множество Наименьшая верхняя грань Непрерывность

Монотонность следует из непрерывности

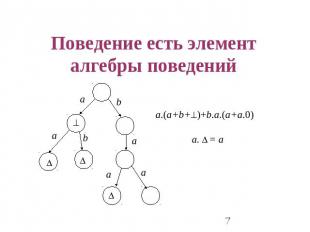
Поведение есть элементалгебры поведений

Как построить алгебру всех поведений произвольных систем над множеством действий А? Алгебра конечных поведенийАлгебра поведений конечной высотыАлгебра бесконечных поведений

Алгебра конечных поведений Ffin(A) Порождается терминальными константами 0, Состоит из выражений в сигнатуре +, (().()) Отношение аппроксимации:

Каноническая форма I – конечное множество индексов, и расходится в противном случае Если все ai. ui различны и ui представлены в такой жеформе, то представление u единственно с точностью докоммутативности недетерминированного выбора. Индукция по высоте терма h(u)

Критерий аппроксимации Индукция по высоте u

Ffin(A) есть инициальная алгебра поведений Свободные алгебры поведений Ffin(A,X)

Алгебра поведений конечной высоты I произвольное множество (может быть пустое) Критерий аппроксимации – определение. Операции:

Полная алгебра поведений F(A) Элементы: классы эквивалентности направленных множеств поведений конечной высоты От классов к представителям. Предел направленного множества направленных множеств = их объединение.Бесконечные суммы:

Каноническая форма в алгебре F(A) Такое представление единственно, если все различны

Теорема о неподвижной точке Добавление переменных:

Следующая лекцияПоведение транзиционных систем Транзиционная система => поведение => транзиционная система