Презентация на тему: Применение систем счисления

МКОУ «Средняя общеобразовательная школа №1 им. А. М. Ижаева с. Учкекен»Обобщающий урок«Применение систем счисления»Информатика 10 класс

Применение систем счисления

РазминкаКогда 2*2 =100?Ответ: в двоичной системе: 210=102, 102*102=1002Как, не производя никаких действий, выполнить операции;а) умножения любого двоичного числа на 2; б) деления любого двоичного числа на 2 с остатком Ответ: а) приписать справа 0, так как 210=102 б) отбросить справа 0, так как 210=102

Какая система?«Я окончил курс университета 44 лет от роду. Спустя год, 100-летним молодым человеком, я женился на 34-летней девушке. Незначительная разница в возрасте — всего 11 лет — способствовала тому, что мы жили общими интересами и мечтами. Спустя немного лет у меня была уже и маленькая семья из 10 детей. Жалования я получал в месяц всего 200 рублей Ответ: в пятеричной системе счисления: 445=2410, 1005=2510, 345=1910, 115=610, 105=510, 2005=10010…

Отгадай«Отгадать целое число в промежутке от 1 до 100. Можно задавать вопросы, на которые -ответы «да» или «нет». Сколько вопросов минимально необходимо задать, чтобы отгадать это число»Решение:Поскольку дана возможность использовать ответы «да» или «нет», то логично предположить, что для кодирования можно использовать двоичную систему счисления. Любое натуральное число от 1 до 100 можно записать при помощи 7 знаков в двоичной системе счисления. 26=64, 27=128Ответ. Минимально достаточно задать 7 вопросов.

Система счисления и банкВы банкир и завтра ждете важного клиента, которому вы должны выдать круглую или не очень круглую в течение 5 минут, но заранее вам неизвестную сумму от 1 до 1 000 000 000 у. е. Вы заранее дали указание своим кассирам заготовить некоторое количество конвертов с деньгами, на которых написаны содержащиеся в них суммы, и собираетесь просто отдать клиенту один или несколько конвертов, в которых и будет содержаться требуемая им сумма. Какое наименьшее количество конвертов необходимо иметь?Вариант 1. Заготовить конверты со всеми суммами от 1 до 1 000 000 000. Но где взять столько денег на конверты?

Вариант 2. Двоичная система. 1конверт- 1 у.е., 2к -2 у.е, 3к- 4 у.е., 4к- 16 у.е., 5к-32 у.е.,…., 11к -1024 у. е 30 к= 536 870 912 у. е. Всего: 30 конвертов

Это алгоритм выдачи сдачи клиенту, записанный некогда даже в инструкции для работников торговли, но очень редко ими выполняющийся( проверьте )Сдачу надо выдавать, начиная с самых больших купюр. Найти конверт с наибольшей суммой денег, не превосходящей требуемую, т.е. наибольшую степень двойки, не превосходящую требуемого количества денег. Если требуемая сумма равна этой степени, то алгоритм заканчивает работу. В противном случае опять выбирается конверт с наибольшей суммой денег, не превосходящей оставшуюся, и т.д. Алгоритм закончит работу, когда останется сумма, в точности равная степени двойки, и она будет выдана последним конвертом.

Или короче…Перевести требуемую сумму в двоичную систему.Расположить конверты от больших сумм к меньшим.Если в переведенном числе 1-берем конверт, 0-не берем.5 минут хватит (надо запросить премию за сообразительность )

СдачаУ вас магазин «Сто мелочей». Цена любого товара не более 300 рублей. Сколько должно быть минимум ячеек в кассе и какие банкноты там?» Решение:300 — (1 + 2 + 4 + 8 + 16 + 32 + 64 + 128) = 300 — 255 = 45 к.Но… нет монет и банкнот с такими номиналами

Какое наименьшее число гирь потребуется для взвешивания любого предмета, масса которого равна целому числу от 1 до 40. Гири разрешено складывать на одну чашу весов». (Задача Баше де Мезириака)Какое наименьшее число гирь потребуется для взвешивания любого предмета, масса которого равна целому числу от 1 до 40. Гири разрешено складывать на одну чашу весов». (Задача Баше де Мезириака)

За какое наименьшее количество взвешиваний на чашечных весах можно отвесить 1 кг сахара, если имеется лишь одна гирька в 1 г ?Вариант 1. Отвесить 1 г, положить в эту же чашку гирьку, отвесить в другой чашке два грамма, переложить гирьку в нее и т.д., добавляя по одному грамму, после тысячного взвешивания отмерить наконец-то килограммВариант 2. Если мы научились отвешивать за n взвешиваний m г песка, то, сделав еще одно взвешивание, можно, даже не используя гирьку, отвесить еще m г и, ссыпав обе порции вместе, получить 2m г за n + 1 взвешивание. Вариант 3. Двоичная система . 1000 = 29 + 28 + 27 + 26 + 25 +23.Так как 29 + 28 + 27 + 26 + 25 + 23 = (((((2 + 1)2 + 1)2 + 1)2 + 1)22 + 1)23, то, последовательно отвешивая 1, 2 + 1 = 3, 2 * 3 + 1 = 7, 2 * 7 + 1 = 15, 2 * 15 + 1 = 31, 2 * 31 = 62, 2 * 62 + 1 = 125, 2 * 125 = 250, 2 * 250 = 500, получаем на десятом взвешивании 2 * 500 = 1000 г.

ТорговцыДвое торговцев заключили соглашение о том, что в течение месяца первый будет давать второму по 10 000 рублей в день. Второй же должен возвращать первому в первый день один копейку, во второй-две и т. д. Второй торговец согласился (жадность )И через сколько дней второй разорился?первые три недели радовался доходам, но в конце месяца был полностью разорён, отдав всё своё состояние первому.

За что будем платить?Человек покупает коня, но недоволен ценой в 1000 рублей. Продавец ему предлагает платить не за коня, а за подковные гвозди,  полушка за первый, две за второй, копейка за третий и так далее. Поскольку в каждой подкове по 6 гвоздей, покупатель вынужден заплатить более….

Цезарь и полководец Когда храбрый полководец вернулся в из сражений, Цезарь спросил, какую плату он хочет за свою службу. Полководец запросил заоблачную сумму. Цезарь, чтобы не прослыть скрягой или человеком, не держащим слово, предложил полководцу пойти на следующий день в казну и взять одну золотую монету весом в один грамм, через день — два грамма и т. д., пока тот сможет сам уносить полученные монеты (каждый день отливаются монеты нужного веса). Полководец, решив что ему удастся легко разбогатеть, согласился. Однако на 18-й день он уже не смог унести монету и в результате получил только малую часть того вознаграждения, что просил у Цезаря. 

Шахматы и двоичная системаЛегенда об изобретателе шахмат гласит, что он скромно попросил себе в награду положить одно зерно на угловую клетку шахматной доски и удваивать количество зерен на каждой следующей клетке. Магараджа, подивившись скудоумию казавшегося таким мудрым человека, распорядился отсыпать ему запрошенные несколько мешков зерна.Смог махараджа расплатиться? Обоснуйте ответ

Доска имеет 64 клеткиили 18 446 744 073 709 551 615 Вес 1 зернышка=0,065 гили 1,200 триллионов тонн(амбар с размерами 10х10х15 км)В мире за год производится 700 млн тонн(1800лет)В отместку правитель, чтобы взять реванш над пытавшимся его обхитрить изобретателем, велел последнему пересчитать каждое зёрнышко, чтобы не было сомнений в том, что он честно с ним расплатился.

Пропагандистом двоичной системы был знаменитый Г.В. Лейбниц (получивший, кстати, от Петра I звание тайного советника).Он отмечал особую простоту действий в двоичной арифметике в и придавал ей определенный философский смысл. Говорят, что по его предложению была выбита медаль с надписью: “Для того чтобы вывести из ничтожества все, достаточно единицы”.

Троичная уравновешенная системаЗадача :Найти такой набор из 4 гирь, чтобы с их помощью на чашечках равноплечных весов можно было взвесить груз массой от 1 до 40 кг включительно. Гири можно располагать на любой чашке весов.

Троичная уравновешенная система1гиря справа 0гиря снята– 1гиря слева Веса гирь:1 кг, 3 кг, 9 кг, 27 кг (идеальная система весов)Пример:27 кг + 9 кг + 3 кг + 1 кг = 40 кг 1 1 1 13ур =Реализация:ЭВМ «Сетунь», Н.П. Брусенцов (1958)50 промышленных образцов

История троичной системы1170—1250 гг., Фибоначчи(Леонардо Пизанский) сформулировал «задачу о гирях»(«задача Баше-Менделеева») и доказал, что, при разрешении класть гири только на одну чашу весов, наиболее экономичной является двоичная система счисления, а при разрешении класть гири на обе чаши весов, наиболее экономичной является троичная симметричная система счисления1840 г. Томас Фоулер(англ.) построил механическую троичную вычислительную машину, одну из самых ранних механических вычислительных машин.1956—1958 г. Н. П. Брусенцов из МГУ построил первую серийную электронную троичную ЭВМ (компьютер) «Сетунь»  работавшую в двухбитном троичном коде, четвёртое состояние двух битов не использовалось. 1973 - en:Ternac, создан в SUNY, Buffalo, США. Экспериментальный троичный компьютер, 2008 г. (14 марта — 24 мая) построена 3-х цифровая компьютерная система TCA2

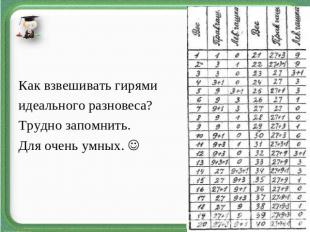
Как взвешивать гирями идеального разновеса?Трудно запомнить.Для очень умных.

Фибоначчиева система счисленияОна основывается на числах Фибоначчи. Числа Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55, … (каждый член, начиная с третьего, равен сумме двух предыдущих). Используемые цифры (алфавит) — только 0 и 1. Хотя для записи числа в этой системе счисления используются только цифры 0 и 1, эту запись нельзя считать двоичным представлением числа. Числа Фибоначчи-числа "золотой пропорции"

Литература Наука и жизнь» №12, 2000гЧеревко К. Е. О происхождении шахмат.Шахматы в СССР.1984,№ 1Бедный торговец. “Информатика” № 3/2005Андреева Е.В., Босова Л.Л., Фалина И.Н. Арифметические основы информатики. М.: БИНОМ. Лаборатория знаний, 2005. Список Интерне ресурсовhttp://www.gifmania.ru http://miranimashek.com

Автор:Боташева Айшат ХанапиевнаУчитель информатикиКЧР, Малокарачаевский район, село УчкекенМКОУ «СОШ №1 им. А. Ижаева с. Учкекен»